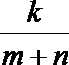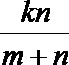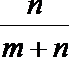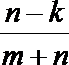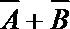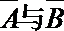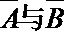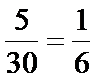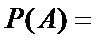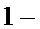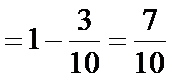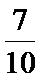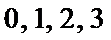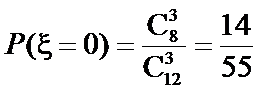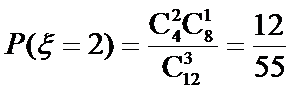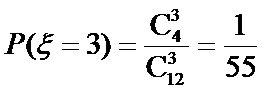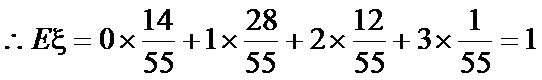1.某班委会由4名男生与3名女生组成,现从中选出2人担任正、副班长,其中至少有1名女生当选的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一个口袋里装有m个白球,n个黑球,从口袋中每次拿出一个球,不放回,第k次拿到黑球的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.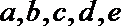
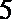

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.随机变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.有编号分别为1,2,3,4,5的5个红球和5个黑球,从中取出4个,则取出的球的编号互不相同的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某国际科研合作项目由两个美国人,一个法国人和一个中国人共同开发完成,现从中随机选出两个人作为成果发布人,现选出的两人中有中国人的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在一个袋子中装有分别标注1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同,同时从中随机取出2个小球,则取出小球标注的数字之差绝对值为2或4的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.投掷一枚质地均匀的骰子两次,若第一次面向上的点数小于第二次面向上的点数我们称其为正实验,若第二次面向上的点数小于第一次面向上的点数我们称其为负实验,若两次面向上的点数相等我们称其为无效。那么一个人投掷该骰子两次后出现无效的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.右面的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.某单位在一次春游踏青中,开展有奖答题活动.从2道文史题和3道理科题中不放回依次抽取2道题,在第一次抽到理科题的前提下第二次抽到理科题的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.同时掷两个骰子,其中向上的点数之和是5的概率( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如果事件A,B互斥,那么( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.从一副扑克牌(52张)中随机抽取2张,则“抽出的2张不是同一花色”的概率为__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.两部不同的长篇小说各由第一、二、三、四卷组成,每卷1本,共8本.将它们任意地排成一排,左边4本恰好都属于同一部小说的概率是 __________(结果用分数表示).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在区间

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.连续抛掷同一骰子两次,出现“点数之和为合数”的概率为__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为



(Ⅰ)求该选手进入第四轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率.(注:本小题结果可用分数表示)
正确答案
(Ⅰ)记“该选手能正确回答第







(Ⅱ)该选手至多进入第三轮考核的概率

解析
解析已在路上飞奔,马上就到!
知识点
20.用一台自动机床加工一批螺母,从中抽出100个逐个进行直径检验,结果如下:
从这100个螺母中,任意抽取1个,求事件A(6.92<d≤6.94)事件B(6.90<d≤6.96)、事件C(d>6.96)、事件D(d≤6.89)的频率。
正确答案
事件A的频率P(A)=
事件B的频率
P(B)=
事件C的频率P(C)=
事件D的频率P(D)=
解析
解析已在路上飞奔,马上就到!
知识点
21.某射击比赛,开始时在距目标100米处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150米处,这时命中记2分,且停止射击;若第二次仍未命中还可以进行第三次射击,但此时目标已在200米处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分。已知射手在100米处击中目标的概率为
(1)求这名射手在射击比赛中命中目标的概率;
(2)求这名射手在比赛中得分的数学期望。
正确答案
记“第一、二、三次射击命中目标”分别为事件A,B,C,
“三次都未击中”为事件D,
则P(A)= 
则P(x)=
因为 x=100时
P(A)=
所以k=5000,
P(x)=
P(B)= 
P(C)=
P(D)=
(1)为1-P(D)=
(2)

解析
解析已在路上飞奔,马上就到!
知识点
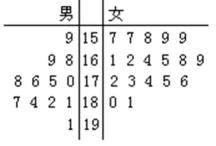
17.第七届城市运动会2011年10月16日在江西南昌举行 ,为了搞好接待工作,运动会组委会在某大学招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”, 身高在175cm以下(不包括175cm)定义为“ 非高个子 ”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用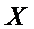
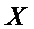
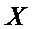
正确答案
(1)根据茎叶图,有“高个子”12人,“非高个子”18人
用分层抽样的方法,每个人被抽中的概率是
所以选中的“高个子”有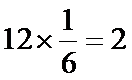
“非高个子”有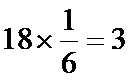
用事件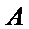
则它的对立事件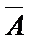
“没有一名“高个子”被选中”
则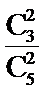
因此,至少有一人是“高个子”的概率是
(2)依题意,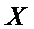
根据茎叶图可知男的高个子有8人,女的有4人;
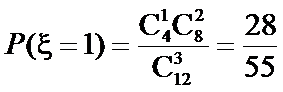
因此,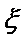
解析
解析已在路上飞奔,马上就到!
知识点
22.甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
正确答案
(1)甲校两男教师分别用A、B表示,女教师用C表示;
乙校男教师用D表示,两女教师分别用E、F表示
从甲校和乙校报名的教师中各任选1名的所有可能的结果为:
{A,D}{A,E},{A,F},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F}共9种。
从中选出两名教师性别相同的结果有:{A,D},{B,D},{C,E},{C,F}共4种,
选出的两名教师性别相同的概率为
(2)从甲校和乙校报名的教师中任选2名的所有可能的结果为:
{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},
{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15种,
从中选出两名教师来自同一学校的结果有:
{A,B},{A,C},{B,C},{D,E},{D,F},{E,F}共6种,
选出的两名教师来自同一学校的概率为
解析
解析已在路上飞奔,马上就到!
知识点
19.甲、乙两位篮球运动员进行定点投蓝,每人各投4个球,甲投篮命中的概率为

(1)求甲至多命中2个且乙至少命中2个的概率;
(2) 求甲比乙投中的球恰好多两个的概率。
正确答案
(1)设“甲至多命中2个球”为事件A,
“乙至少命中两个球”为事件B,
由题意得,
∴甲至多命中2个球且乙至少命中2个球的概率为
(2)设甲比乙投中的球恰好多两个为事件C
则
P(C)=
解析
解析已在路上飞奔,马上就到!