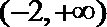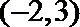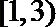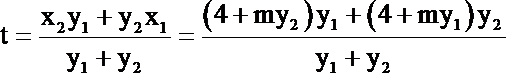1.若集合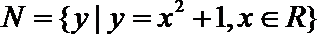
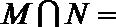
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 关于


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.阅读下面程序框图,如果输出的函数值在区间

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.直线











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若圆C:


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数①

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知z=2x +y,x,y满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设F1, F2分别为双曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.平面四边形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数f(x)是定义在R上的以4为周期的函数,”当x∈(-1,3]时,f(x)=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 对于函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知向量

正确答案
-8
解析
解析已在路上飞奔,马上就到!
知识点
15.在等差数列





正确答案
-2013
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数f(x)=x2-1,对任意x∈[

正确答案
(-∞,-

解析
解析已在路上飞奔,马上就到!
知识点
13.一个几何体的三视图如图所示,则这个几何体的表面积与其外接球面积之比为________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
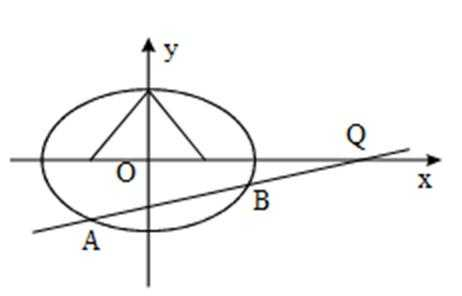
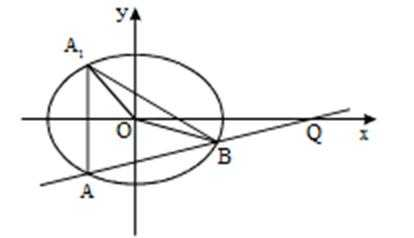
20.如图,已知椭圆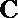
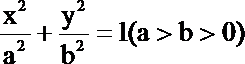
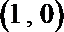
(Ⅰ)求椭圆
(Ⅱ)过点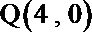
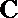
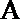


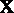
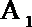
(ⅰ)求证:直线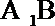
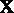
(ⅱ)求△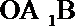
正确答案
解:
(Ⅰ)因为椭圆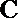
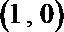
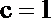
椭圆两个焦点与短轴的一个端点构成等边三角形.
所以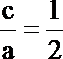
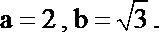
所以椭圆的标准方程为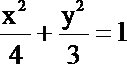
(Ⅱ)(i)设直线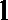
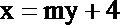

得: 
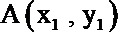
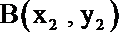
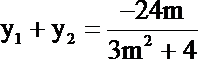
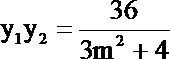
由A关于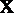
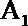
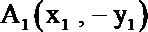
根据题设条件设定点为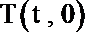
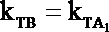
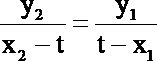
所以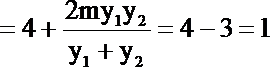
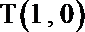
(ii)由(i)中判别式
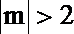
可知直线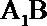

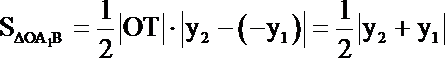
得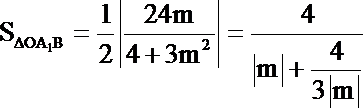

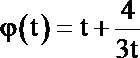
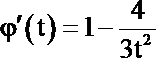
当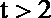
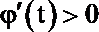
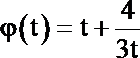

所以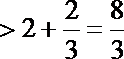
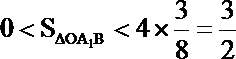
故△OA1B的面积取值范围是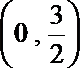
解析
解析已在路上飞奔,马上就到!
知识点
17.已知










(Ⅰ)若



(Ⅱ)若



正确答案
解:(Ⅰ)




又






又

(Ⅱ)在







又






解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数





(Ⅰ)求
(Ⅱ)求
(Ⅲ)设




正确答案
解:(Ⅰ)

(Ⅱ)此时


所以



当



当 



所以,增区间为(0,1) 减区间为(1,
(Ⅲ)


记



当



当



所以,

记




所以,

综①、②知,
解析
解析已在路上飞奔,马上就到!
知识点
18.设公比大于零的等比数列










(Ⅰ)求数列

(Ⅱ)设


正确答案
解:(Ⅰ)由


又

则得
所以

(Ⅱ)


设,若数列

则

即

当



解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在
(1)若点P为AB的中点,E为
(2)当棱锥
正确答案
解:
(1)证明:作
由已知得:


所以
(2)设

令
则
由上表易知:当

解析
解析已在路上飞奔,马上就到!
知识点
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分
22.如图,⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
(1)求证:AD//EC;
(2)若AD是⊙O2的切线,且PA=6,PC =2,BD =9,求AD的长。
23.在平面直角坐标系







(Ⅰ)求曲线
(Ⅱ)设直线





24.已知不等式

(Ⅰ )求
(Ⅱ )若

正确答案
22.
(1)证明:连接



又
(2)













23.
解:(Ⅰ)由

当


当



∴曲线

(Ⅱ)把直线

得

由于


∵直线



24.
解:(Ⅰ)依题意,当


经检验,
(Ⅱ)由(Ⅰ)知
根据柯西不等式,得
所以
当且仅当



因此

解析
解析已在路上飞奔,马上就到!