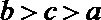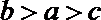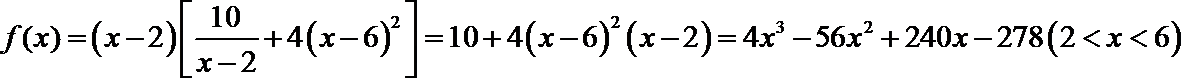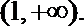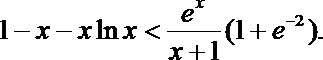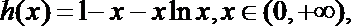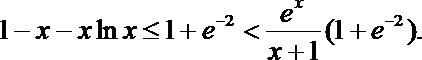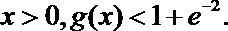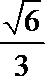5. 如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:
①
②
③ 
④ 
其中“同簇函数”的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 如图,矩形OABC内的阴影部分是由曲线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知i是虚数单位,则复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 若点



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 在等差数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.某几何体的三视图如图所示,图中的四边形都是边长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 如图,










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 在等腰梯形











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知双曲线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 可导函数
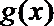

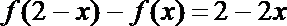
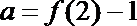



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 在等差数列








(1)求

(2)设数列




正确答案
(1)设

因为
解得 

故
(2)由(1)可知,
所以
故
解析
解析已在路上飞奔,马上就到!
知识点
20. 时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量




(1)求
(2)假设网校的员工工资、办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格
正确答案
(1)因为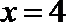

代入关系式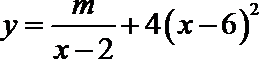

解得
(2)由(1)可知,套题每日的销售量
所以每日销售套题所获得的利润
,从而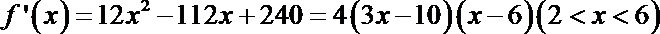
令

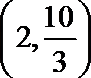





所以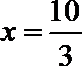
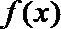
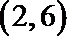
所以当

故当销售价格为3.3元/套时,网校每日销售套题所获得的利润最大.
解析
解析已在路上飞奔,马上就到!
知识点
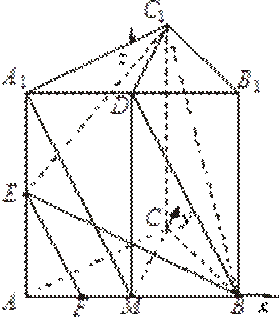
19. 在三棱柱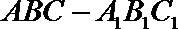

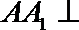
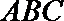
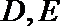
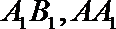
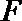


(1)求证: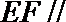

(2)求二面角
正确答案
(1)证明:取

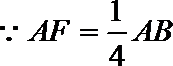
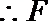
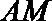
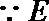
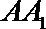

在三棱柱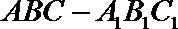



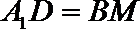
则四边形






则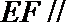
(2)空间直角坐标系,则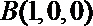

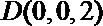
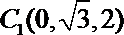
∴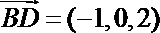
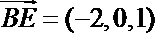

设面BC1D的一个法向量为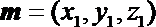
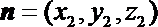
则由


又由

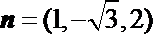
则
故二面角E-BC1-D的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数

(1)若


(2)设











正确答案
(1)
令




当


(2)




所以
因为
由余弦定理得
解得:
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知椭圆


(Ⅰ)求椭圆
(Ⅱ)设直线






正确答案
(Ⅰ)设椭圆的半焦距为
∴ 

(Ⅱ)设

(1)当

(2)当



由已知

把




当且仅当



综上所述
所以,当


解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数


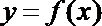


(1)求
(2)求
(3)设
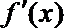



正确答案
(1)由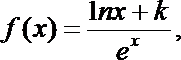
由于曲线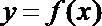

所以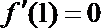
(2)由(1)得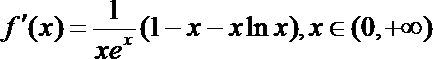
令


当


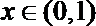
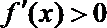
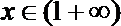

因此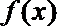
(3)证明:因为
所以
因此对任意
由(2)知
所以
因此当



所以


因为


故


因此对任意
解析
解析已在路上飞奔,马上就到!
知识点
13. 对大于或等于2的正整数的幂运算有如下分解方式:






根据上述分解规律,若


正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
15. 
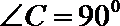

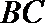


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知函数
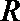

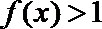
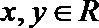
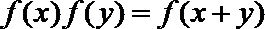

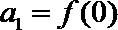

正确答案
4017
解析
解析已在路上飞奔,马上就到!