数学宝山区2012年高三试卷

精品

填空题
简答题
单选题

立即下载

数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、简答题

3、单选题

真题试卷
模拟试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

5．将函数的图象上各点的横坐标伸长到原来的2倍（纵坐标不变），再向左平移个单位，所得函数的解析式为____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

7．无穷数列中，若，则=______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 4分

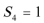
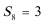
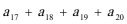
9．在等比数列{an}中，，，则的值是____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义

题型：填空题

分值: 4分

10．方程在的解集为____________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 4分

1．抛物线的准线方程是____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

2．化简行列式为____________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

3．若A为阶矩阵，AB=C，则B的阶数可以是下列中的____________．

①，②，③，④．

正确答案

③④

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面垂直的判定与性质

题型：填空题

分值: 4分

4．若函数的反函数的图像过点（2，－1），则a=____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

6．二项式展开式中的前三项系数成等差数列，则的值为______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义域

题型：填空题

分值: 4分

8．函数，的单调递增区间是____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：填空题

分值: 4分

11．已知关于的不等式的解集是，则实数的取值范围是____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：填空题

分值: 4分

12．方程的实数解的个数为____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 4分

13．阅读下列材料：若两个正实数满足,那么。证明：构造函数，因为对一切实数，恒有,所以，从而得,所以。根据上述证明方法,若个正实数满足时，你能得到的结论为_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

14．设为数列的前项和，若不等式对任意等差数列及任意正整数都成立，则实数的最大值为____________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱的结构特征

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19．记函数f（x）=的定义域为A, 的定义域为B．若AB，求实数m的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用

题型：简答题

分值: 14分

20．△中，已知，边，设，△的周长为．

（1）求函数的解析式，并写出函数的定义域；

（2）求函数的值域。

正确答案

（1）△ABC的内角和A+B+C=，且，

由正弦定理，知即

所以

（2）由（1）知，

由正弦函数的图像知，当时，有．

于是，，

所以，函数的值域是

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 14分

21．已知数列的前项和为，对一切正整数，点都在函数的图象上。

（1）求数列的通项公式；

（2）若，求数列的前项和为；

（3）设，数列的前项和，求的值。

正确答案

（1）因为点都在函数的图象上

所以

当时，

当时，（*）

令，，也满足（*）式

所以，数列的通项公式是．

（2）

（3）因为，则数列成公比为等比数列的等比数列。

当时，；

；

当时，

当时，-

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域

题型：简答题

分值: 16分

22．设m为实数，函数，．

（1）若≥4，求m的取值范围；

（2）当m＞0时，求证在上是单调递增函数；

（3）若对于一切，不等式恒成立，求实数m的取值范围．

正确答案

（1）

当时，，无解；

当时，，解得。

所以。

（2）由于。所以。

任取，

所以即：在为单调递增函数。

解二：由（2）结论得：是单调递增函数，所以只要，

得，当时不等式显然成立；当时，解得：，

综上得：．

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：简答题

分值: 18分

23．已知函数，方程的根称为函数的不动点；若，则称为由函数导出的数列。

设函数，

（1）求函数的不动点；

（2）设，是由函数导出的数列，对⑴中的两个不动点（不妨设），设，求数列的通项公式，并求；

（3）试探究由函数导出的数列，（其中）为周期数列的充要条件。

注：已知数列，若存在正整数，对一切都有，则称数列为周期数列，是它的一个周期。

正确答案

（1），即，得；

所以，函数的不动点为。

（2），，设，

则

，=4。

所以，数列是等比数列，首项为4，公比为。

，得，

（3），即，

因为所以该方程有两个不相等的实数根。

则数列是等比数列，首项为，公比为。

因为，所以

数列为周期数列的充要条件是，即

故，但，从而，

所以

解析

解析已在路上飞奔，马上就到！

知识点

变化的快慢与变化率

单选题本大题共4小题，每小题5分，共20分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

15．已知函数的大致图像如图，则函数的奇偶性是（　　）

A一定是偶函数

B一定是奇函数

C既是奇函数也是偶函数

D既不是奇函数也不是偶函数

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

16．设若的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

17．已知是定义域为正整数集的函数，对于定义域内任意的，若成立，则成立，下列命题成立的是（）

A若成立，则对于任意，均有成立；

B若成立，则对于任意的，均有成立；

C若成立，则对于任意的，均有成立；

D若成立，则对于任意的，均有成立

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

18．若直角坐标平面内的两点P．Q满足条件：

①P．Q都在函数的图像上；

②P．Q关于原点对称，则称点对（P，Q）是函数的一个“友好点对”（点对（P，Q）与（Q，P）看作同一个“友好点对”）。

已知函数则此函数的“友好点对”有____________对。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

奇偶函数图象的对称性

数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

数学热门试卷