3.函数f(x)=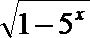
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知奇函数f (x)的定义域为R, 且对于任意实数x都有f(x+4)=f(x)成立, 又f (1)=4, 那么f [f ( 7 ) ]等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集U={-2,-1,1,0,1,2},A={-2,-1,0},B={0,1,2},则(
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.为了得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在区间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知p:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.对任意的


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数f(x)=1-x2 (x<0),则f -1(-3)=______________
正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
10.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知奇函数f(x)在(0, +∞)单调递增,且f(3)=0,则不等式x·f(x)<0的解集是______________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.奇函数


正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
13.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若函数f (x)=lg(ax2-4x+a-3)的值域是一切实数,则a的取值范围是______
正确答案
[0,4]
解析
解析已在路上飞奔,马上就到!
知识点
15.二次函数f(x)满足
(1)求f(x)的解析式;
(2)在区间
正确答案
(1)设f(x)=ax2+bx+c,
由f(0)=1得c=1,故f(x)=ax2+bx+1.
∵ f(x+1)-f(x)=2x,
∴ a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x,
所以
∴ f(x)=x2-x+1.
(2)由题意得x2-x+1>2x+m在[-1,1]上恒成立.
即x2-3x+1-m>0在[-1,1]上恒成立.
设g(x)= x2-3x+1-m,
其图象的对称轴为直线x=
所以g(x) 在[-1,1]上递减.
故只需g(1)>0,
即12-3×1+1-m>0,
解得m<-1.
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数


正确答案
由二次函数的图象与性质得f(x)的图象对称轴是x=m/2且开口向上;
所以f(x)在区间(-∞,m/2]上单调递减,
在区间[m/2, +∞)上单调递增;
(1)当
[f(x)] min=f(m/2)=2-2m=5
解得

(2)当


所以,
解之得:

所以,
(3)当


所以,
解之得:
综上,当


解析
解析已在路上飞奔,马上就到!
知识点
16.已知f (x)=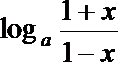
(1)求f (x)的定义域;
(2)判断f (x)的奇偶性并给予证明;
(3)求使f (x)>0的x的取值范围
正确答案
(1) 由 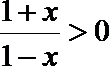
∴ f (x)的定义域为(-1,1)
(2) ∵ f (x)的定义域为(-1,1)关于原点对称;
且 f (-x)=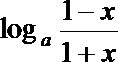
∴ 函数y=f (x)是奇函数;
(3) 由f (x)=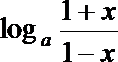
若a>1, 则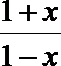
即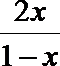
∴ 0<x<1;
若0<a<1, 则 0<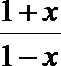
∴-1<x<0
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(1)求函数
(2)求函数
正确答案
(1)由函数的图像经过点(0,2)可知,
∴ f(x)=x3+bx2+cx+2
∴ f ′(x)=3x2+2bx+c
∵ 

∴ 
故所求的解析式是
(2)由(1)∴ f′(x)=3x2- 6x -3
令3x2- 6x -3=0 ,即 x2-2x -1=0
解得 x1=
当x< 

当

故函数
(-∞,

单调递减区间是(

解析
解析已在路上飞奔,马上就到!
知识点
19.用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少
正确答案
设容器的高为xcm,容器的体积为V(x)cm3,
则V(x)=(90-2x)(48-2x)x,
V(x)=4x3-276x2+4320x (0<V<24)
∵ V′(x) =12 x2-552x+4320=12(x-10)(x-36)
由V′(x)=0得x1=10,x2=36 (舍去)
∵ 当0<x<10 时,V′(x)>0,那么V(x)为增函数
当10<x<24时,V′(x)<0, 那么V(x)为减函数
所以,当x=10, V(x)有极大值V(10)=10(90-20)(48-20)=1960
又V(0)=0,V(24)=0,
所以当x=10, V(x)有最大值V(10)=1960
∴ 容器的高为10cm时,容器的容积最大,最大容积是1960cm3
解析
解析已在路上飞奔,马上就到!
知识点
20.已知定义在




(1)计算
(2)证明f (x)在
(3)当
正确答案
(1)由题意,令m=n=1, 则f(1)= f(1) +f(1),所以f(1)=0.
(2)设
即
因为




于是

(3)因为
所以
因为

所以
解得 

故所求不等式的解集为
解析
解析已在路上飞奔,马上就到!