3.若非空集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设数列








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.集合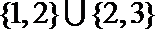
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如果函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.化简
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.将9个数排成如右图所示的数表,若每行3个数按从左至右的顺序构成等差数列,每列的3个数按从上到下的顺序也构成等差数列,且表正中间一个数a22=2,则表中所有数之和为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.等比数列





正确答案
1或
解析
解析已在路上飞奔,马上就到!
知识点
14.如果函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知在数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 在等比数列

(I)求数列
(II)若数列





正确答案
(I)an=

(II)
解析
解析已在路上飞奔,马上就到!
知识点
21. 设数列


(I)求数列
(II)设



正确答案


(Ⅱ)∵
∴


④-③得

即

解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数

(1)求常数
(2)解不等式
正确答案
(1)因为
所以
由


(2)由(Ⅰ)得
解析
解析已在路上飞奔,马上就到!
知识点
19. 在某种工业品的生产过程中,每日次品数




正确答案
设利润函数为
显然
只有一个极值点,所以也是要求的最大值点,所以为了获得最大利润,日产量应定为
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知函数
(1)当


(2)若


正确答案
(1)

又



(2)由于
若令
有

要使
即
解析
解析已在路上飞奔,马上就到!
知识点
22. 设二次函数
①当



②当

(I)求
(II)求
(III)是否存在实数



正确答案
(I)在②中令x=1,有1≤f(1)≤1,故f(1)=1.
(II)由①知二次函数的关于直线对称,且开口向上,
故设此二次函数为

∵f(1)=1,
∴
∴

(III)假设存在t∈R,当

令

则 不等式

有下列几种情况:
(1)当


所以只需

解得
所以 
(2)当



所以只需

解得
所以 
(3)当


所以只需

解得
所以 
∴综上所述,存在实数t且
解析
解析已在路上飞奔,马上就到!



































































