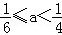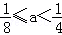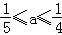1.函数
正确答案
[0,+∞)
解析
解析已在路上飞奔,马上就到!
知识点
2.x>1是
正确答案
充分不必要条件
解析
解析已在路上飞奔,马上就到!
知识点
3.方程
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
4.已知α是第二象限的角,tanα=﹣
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若a>3,则a+
正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
7.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.f(x)是定义在R上的奇函数,当x>0时,f(x)=3x,则f(-2)=________
正确答案
﹣9
解析
解析已在路上飞奔,马上就到!
知识点
10.若不等式|x+1|+|x﹣2|≥a恒成立,则a的取值范围是________.
正确答案
a≤3
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数f(x)=
正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
9.已知A,B,C是△ABC的内角,并且有sin2A+sin2B=sin2C+sinAsinB,则C=________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若tan
正确答案
﹣1
解析
解析已在路上飞奔,马上就到!
知识点
11.函数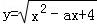
正确答案
{4}
解析
解析已在路上飞奔,马上就到!
知识点
13.对任意实数x,y,定义运算x*y=ax+by+cxy,其中a,b,c是常数,等式右边的运算是通常的加法和乘法运算.已知1*2=3,2*3=4,并且有一个非零常数m,使得对任意实数x,都有x*m=x,则m的值是________.
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.设f(x)的定义域为D,f(x)满足下面两个条件,则称f(x)为闭函数.
①f(x)在D内是单调函数;
②存在[a,b]⊆D,f(x)在[a,b]上的值域为[a,b].
如果f(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.A,B是三角形ABC的两个内角,则“sinA>sinB”是A>B的( )条件.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.a>0,a≠1,函数f(x)=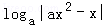
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知集合M={x∈Z|x2≤1},N={x∈R|﹣1<x<2},则M∩N=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知命题P:“函数

(1)若命题P和命题Q同时为真,求实数m的取值范围;
(2)若命题P和命题Q有且只有一个真命题,求实数m的取值范围.
正确答案
(1)∵命题P:“函数
命题Q:“幂函数
∴P:m<1,Q:﹣1<m<3,
∴当命题P和命题Q同时为真时,实数m的取值范围是:﹣1<m<1.
(2)当命题P和命题Q有且仅有一个真时,P真Q假,或P假Q真,
当P真Q假时,
解得实数m的取值范围是:m≤﹣1.
当P真Q假时,
解得实数m的取值范围是:1≤m≤3.
综上所述,若命题P和命题Q有且只有一个真命题,
实数m的取值范围(﹣∞,﹣1]∪[1,3].
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)求函数f(x)的最小正周期;
(2)在△ABC中,已知A为锐角,f(A)=1,
正确答案
(1)由
f(x)=cos2x+sinxcosx=
=




∴T=
(2)∵f(A)=cos2A+sinAcosA=1
移项得:sinAcosA=1﹣cos2A=sin2A,
因为A为锐角,所以sinA≠0
∴sinA=cosA,则
根据正弦定理得:



所以AC=

解析
解析已在路上飞奔,马上就到!
知识点
21.已知定义在区间


(1)求

(2)求y=f(x)的函数表达式;
(3)如果关于x的方程f(x)=a有解,那么将方程在a取某一确定值时所求得的所有解的和记为Ma,求Ma的所有可能取值及相对应的a的取值范围。
正确答案
(1)
(2)∵函数y=f(x)的图象关于直线
又∵当
∴当
f(x)=
(3)作函数f(x)的图象(如图),显然,若f(x)=a有解,则a∈[0,1]
①


③
④a=1,f(x)=a有两解,Ma=
解析
解析已在路上飞奔,马上就到!
知识点
22.我国加入WTO后,根据达成的协议,若干年内某产品关税与市场供应量P的关系允许近似的满足:P(x)=2(1﹣kt)(x﹣b)2(其中t为关税的税率,且

(1)根据图象求k、b的值;
(2)若市场需求量为Q,它近似满足
正确答案
(1)由图可知,
(2)当P=Q时,得
令
∴对称轴m=
∴

∴税率t的最小值为
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数f(x)=
(1)试就实数a的不同取值,写出该函数的单调递增区间;
(2)已知当a>0时,函数在(0,

(3)若函数f(x)在区间
正确答案
(1)①当a<0时,函数f(x)的单调递增区间为(﹣

②当0<a≤1时,函数f(x)的单调递增区间为(﹣∞,0)及(0,+∞),
③当a>1时,函数f(x)的单调递增区间为(﹣∞,﹣

(2)由题设及(1)中③知
且a>1,解得a=3,
因此函数解析式为f(x)=
(3)1#当a(a﹣1)>0即a<0或a>1时
由图象知
解得a∈(﹣∞,

2#当a=1时,函数为正比例函数,故在区间内存在反函数,所以a=1成立.
3#当a(a﹣1)<0,得到



综上a∈∈(﹣∞,



解析
解析已在路上飞奔,马上就到!