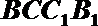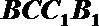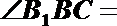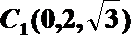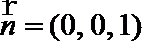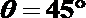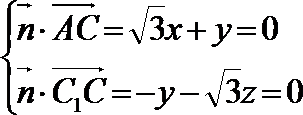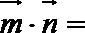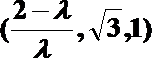19. 设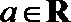
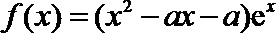
(Ⅰ)若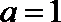
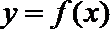
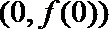
(Ⅱ)求函数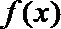
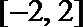
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在等差数列







(Ⅰ)求数列

(Ⅱ)设






正确答案
解:(Ⅰ)设等差数列



由题意,得

∴

(Ⅱ)
∴
∴
∴

令


故


解析
解析已在路上飞奔,马上就到!
知识点
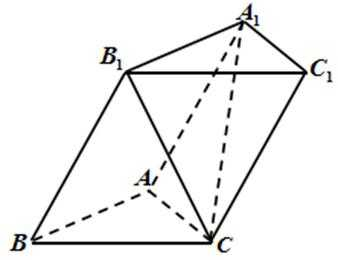
20.如图,三棱柱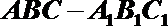
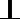
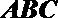
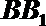
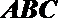
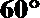
(Ⅰ)求直线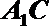
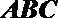
(Ⅱ)在线段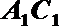
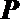
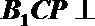
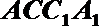
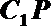
正确答案
解:(Ⅰ)过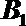

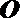
∴
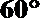
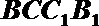
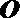
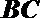
以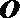
则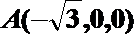
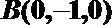
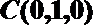


∴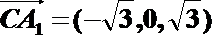
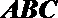
设直线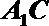
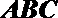
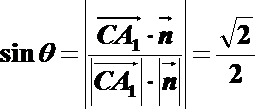
所以,直线

(Ⅱ)假设在线段
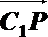

则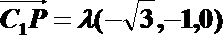
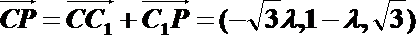
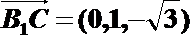
设平面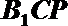

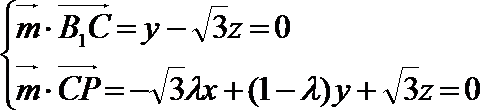
令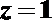
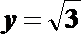
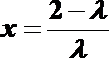
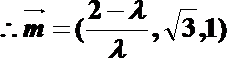
设平面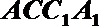

令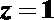
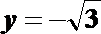
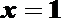

要使平面
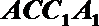
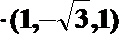


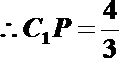
解析
解析已在路上飞奔,马上就到!
知识点
17.在




(1)用
(2)判断
正确答案
解:(1)


则
若

(2)

若




解析
解析已在路上飞奔,马上就到!
知识点
18.甲、乙、丙三人组成一组,参加一个闯关游戏团体赛,三人各自独立闯关,其中甲闯关成功的概率为


(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆


(1)若
(2)设







正确答案
解:(1)由题意得


(2)依题意,

又




因为
所以

(此题也可用

解析
解析已在路上飞奔,马上就到!
知识点
22.已知




(Ⅰ)过坐标原点



(Ⅱ)令



正确答案
解:(I)

所以切线的斜率
整理得
显然,


所以方程

(Ⅱ)

设

易知


(1)当












(2)当



则




又∵
∴


当



从而



∴

解析
解析已在路上飞奔,马上就到!
知识点
4 .设集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7 .下列命题中,真命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.定义在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1 .设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2 .已知等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3 .已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5 .五名同学报考五所名牌大学的自主招生.已知考试分笔试与面试,每人笔试通过的概率都是

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6 .若变量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8 .点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若随机变量







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在棱长为1的正方体



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.函数


正确答案
解析
解析已在路上飞奔,马上就到!