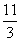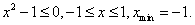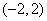1.函数

正确答案
解析
∵
∴
由

故
知识点
3.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知

正确答案
解析
由
可得
所以
知识点
8.方程

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 函数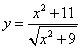
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若对任意正实数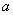
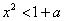
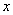
正确答案
-1
解析
因为对任意正实数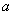
不等式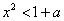
所以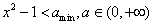
因此
知识点
5.同时满足(1)
正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
6.集合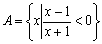
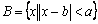
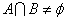
正确答案
解析
“a=1”是“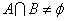
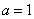
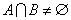
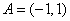
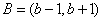
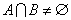
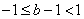
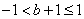
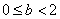
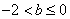
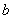
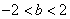
知识点
9. 如果
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数
正确答案

解析
因为函数
对称中心是
因此函数

知识点
11.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知等比数列









正确答案
45
解析
由题意有
对于和

当

对于


这

把
每个都是以

而最小元素为

故在


所以





当

当


由于


所以


知识点
12.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.关于函数
(1)
(2)
(3)
(4)

正确答案
(2),(3)
解析
解析已在路上飞奔,马上就到!
知识点
15.下列说法正确的是( )
正确答案
解析











而
知识点
18.定义一种新运算:



正确答案
解析
这类问题,首先要正确理解新运算,
能通过新运算的定义把新运算转化为我们已经学过的知识,然后解决问题.
本题中

因此


函数

函数

且
因此当



因此
由函数的单调性知


又

且
又

且
函数
说明函数

从函数

知识点
16. 



正确答案
解析
由于当



由题意当

则

因此

知识点
17.如果

正确答案
解析

如果
则


如果
不妨设
则
所以 
知识点
20.在



(1)求
(2)若

正确答案
(1)
(2)
解析
(1)由已知条件结合正弦定理有:
从而有:


(2)由正弦定理得:


即:
知识点
19.解关于x的不等式:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.数列

(1) 求数列
(2) 设





正确答案
(1) 
(2)
解析
(1)
又
则


(2)当

当

知识点
23.已知函数




(1)求函数
(2)求数列{an}、{bn}的通项公式;
(3)若对任意实数

正确答案
(1)
(2)

(3)3
解析
(1)
∴
联立解得
(2)∵

∴

又

相加有
∴
(3)对任意实数λ∈[0,1]时,

则
变形为

设
∴
∴
∴

故kmin=3
知识点
22.阅读:
已知



解法如下:
当且仅当

则

应用上述解法,求解下列问题:
(1)已知


(2)已知

(3)已知正数



求证:
正确答案
(1)9;
(2)18;
(3)证明见解析.
解析
(1)
而
当且仅当
则


(2)
而

当且仅当
即

所以函数

(3)
当且仅当