1．设复数
A
B
C－
D－
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2． 已知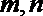
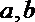
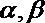
①若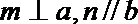
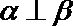
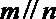
②若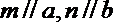
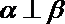
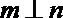
③若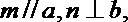
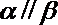
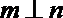
④若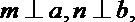
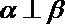
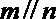
其中真命题的序号是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3． 为得到函数
A向左平移
B向右平移
C向左平移
D向右平移
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7． 已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．在
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．在△ABC中，tanA是第3项为－4，第7项为4的等差数列的公差，tanB是第3项为，第6项为9的等比数列的公比，则△ABC是( )
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6． 一个几何体的正视图、侧视图、俯视图如图所示，则该几何体的表面积和体积分别为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．已知与函数
A
B1
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11． 三棱锥
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12． 函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14.已知A(－2, 3), B(3, 2)，过点P(0, －2)的直线l与线段AB没有公共点，则直线l的斜率的取值范围是____________．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13． 如图，A1B1C1﹣ABC是直三棱柱，∠BCA=90°，点D1、F1分别是A1B1、A1C1的中点，若BC=CA=CC1，则BD1与AF1所成角的余弦值是____________．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15． 在三棱锥P-ABC中，给出下列四个命题：
① 如果PA⊥BC，PB⊥AC，那么点P在平面ABC内的射影是△ABC的垂心；
② 如果点P到ABC的三个顶点的距离都相等，那么点P在平面ABC内的射影是△ABC的内心；
③ 如果棱PA和BC所成的角为60o,PA=BC=2,E、F分别是棱PB、AC的中点,那么EF=1;
④ 如果三棱锥P-ABC的各棱长均为1,则该三棱锥在任意一个平面内的正投影（投影线垂直投影面）的面积都不大于;
其中正确命题的序号是____________．
正确答案
①③④
解析
解析已在路上飞奔，马上就到！
知识点
20．在
（Ⅰ）求
（Ⅱ）求
正确答案
（Ⅰ）
由余弦定理可得：
（Ⅱ）在
解析
解析已在路上飞奔，马上就到！
知识点
19． 某商场销售某种商品的经验表明，该商品每日的销售量
(Ⅰ) 求
(Ⅱ) 若该商品的成品为3元/千克, 试确定销售价格
正确答案
(Ⅰ)因为
(Ⅱ)由(Ⅰ)知该商品每日的销售量
所以商场每日销售该商品所获得的利润：
令
所以当
答：当销售价格
解析
解析已在路上飞奔，马上就到！
知识点
18．已知函数
（1）求函数
（2）若
正确答案
（1）
函数
解析
解析已在路上飞奔，马上就到！
知识点
17．已知等差数列
（1）求数列
（2）若
正确答案
（1）依题意
解得
（2）由（1）可知
所以数列
数列
解析
解析已在路上飞奔，马上就到！
知识点
22．已知函数
（I）求函数
（Ⅱ）函数
（Ⅲ）若任意的
正确答案
（Ⅰ） 
在区间
故
单调递减区间是
（Ⅱ）先求
当
故
由
所以，
（Ⅲ）当
只需证明
也可得证命题成立．
设
设
综上述命题成立．
另解:当
由导数的几何意义有对任意
解析
解析已在路上飞奔，马上就到！
知识点
21．如图，在三棱锥
（1）求证：平面
（2）求直线
（3）若动点
正确答案
（1）取AC中点O,因为AP=BP，
所以OP⊥OC
由已知易得三角形ABC为直角三角形，
∴OA=OB=OC,⊿POA≌⊿POB≌⊿POC,
∴OP⊥OB，∴OP⊥平面ABC,
∵OP在平面PAC中，
∴平面
（2）以O为坐标原点,OB、OC、OP分别为x、y、z轴建立如图所示空间直角坐标系．
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0, 
∴
设平面PBC的法向量
∴ 
∴直线PA与平面PBC所成角的正弦值为
（3）由题意平面PAC的法向量
设平面PAM的法向量为
∵
又因为
∴
解析
解析已在路上飞奔，马上就到！