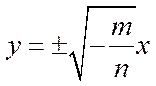
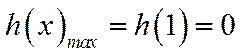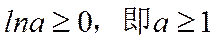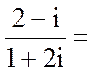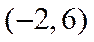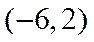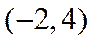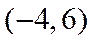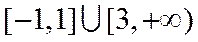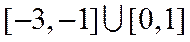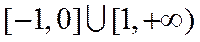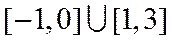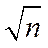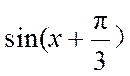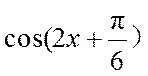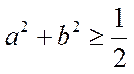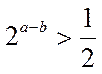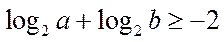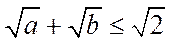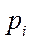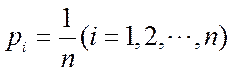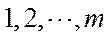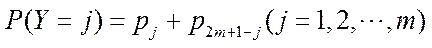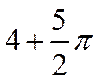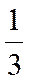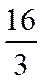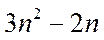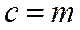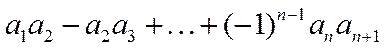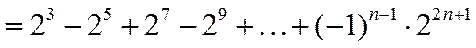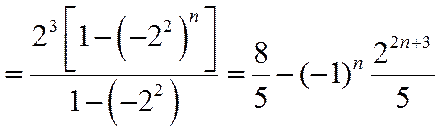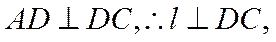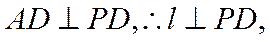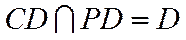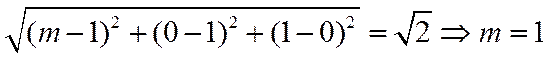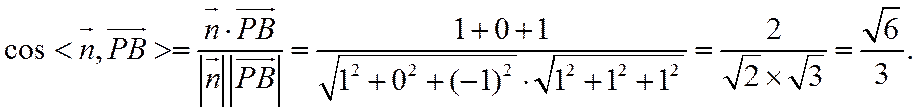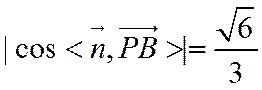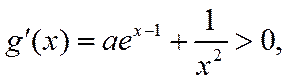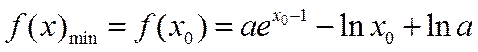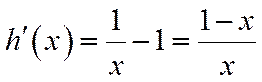2．
正确答案
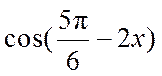
4．日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为
正确答案
6．基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段，可以用指数模型：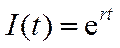
正确答案
7．已知P是边长为2的正六边形ABCDEF内的一点，则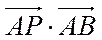
A
B
C
D
正确答案
1．设集合A={x|1≤x≤3}，B={x|2<x<4}，则A∪B=
正确答案
3．6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有
正确答案
5．某中学的学生积极参加体育锻炼，其中有96%的学生喜欢足球或游泳，60%的学生喜欢足球，82%的学生喜欢游泳，则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是
正确答案
8．若定义在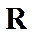
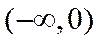
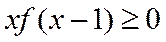
A
B
C
D
正确答案
9．已知曲线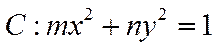
A若m>n>0，则C是椭圆，其焦点在y轴上
B若m=n>0，则C是圆，其半径为
C若mn<0，则C是双曲线，其渐近线方程为
D若m=0，n>0，则C是两条直线
正确答案
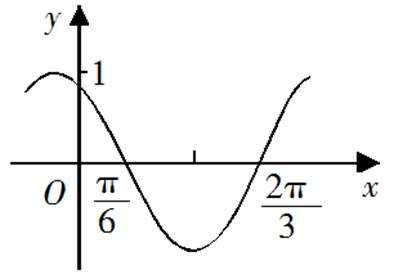
10．下图是函数y= sin(ωx+φ)的部分图像，则sin(ωx+φ)=
A
B
C
D
正确答案
11．已知a>0，b>0，且a+b=1，则
A
B
C
D
正确答案
12．信息熵是信息论中的一个重要概念.设随机变量X所有可能的取值为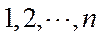
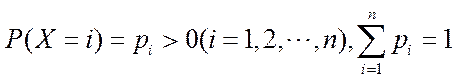
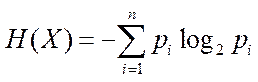
A若n=1，则H(X)=0
B若n=2，则H(X)随着
C若
D若n=2m，随机变量Y所有可能的取值为
正确答案
16．已知直四棱柱ABCD–A1B1C1D1的棱长均为2，∠BAD=60°．以
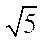
正确答案
13．斜率为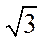
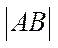
正确答案
14．将数列{2n–1}与{3n–2}的公共项从小到大排列得到数列{an}，则{an}的前n项和为________．
正确答案
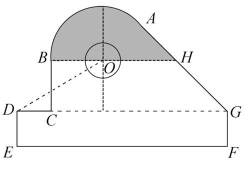
15．某中学开展劳动实习，学生加工制作零件，零件的截面如图所示．O为圆孔及轮廓圆弧AB所在圆的圆心，A是圆弧AB与直线AG的切点，B是圆弧AB与直线BC的切点，四边形DEFG为矩形，BC⊥DG，垂足为C，tan∠ODC=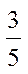
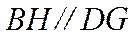
正确答案
17．（10分）
在①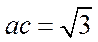
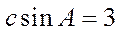
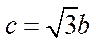
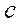
问题：是否存在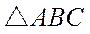
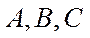
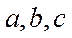
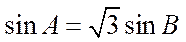
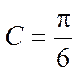
注：如果选择多个条件分别解答，按第一个解答计分．
正确答案
解法一：
由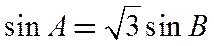
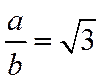
不妨设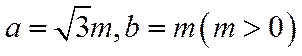
则：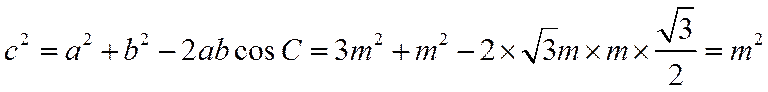
选择条件①的解析：
据此可得：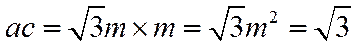
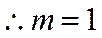
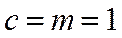
选择条件②的解析：
据此可得：
则：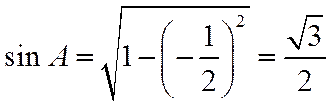
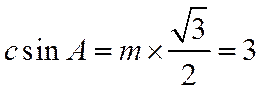
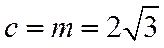
选择条件③的解析：
可得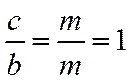
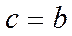
与条件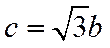
解法二：∵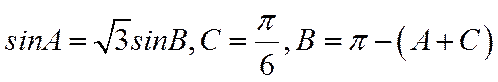
∴
∴
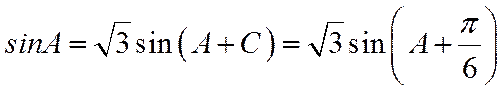
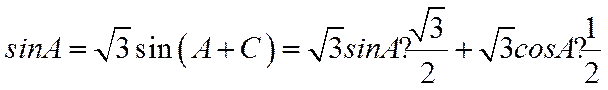
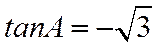
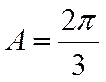
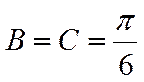
若选①，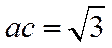
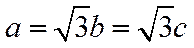
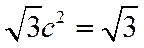
若选②，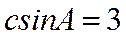
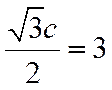
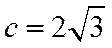
若选③,与条件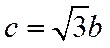
18．（12分）
已知公比大于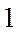
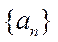
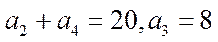
（1） 求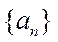
（2） 求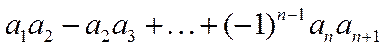
正确答案
(1) 设等比数列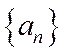
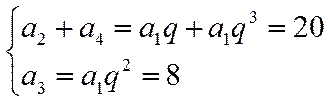
整理可得：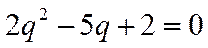
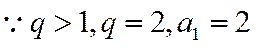
数列的通项公式为：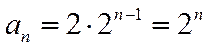
(2)由于：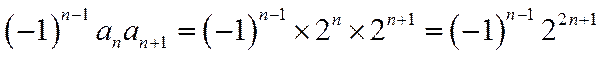
19．（12分）
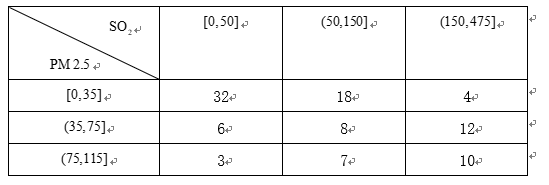
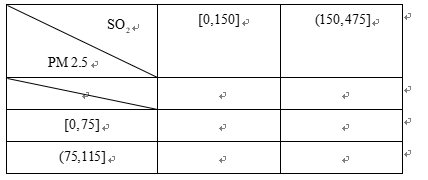
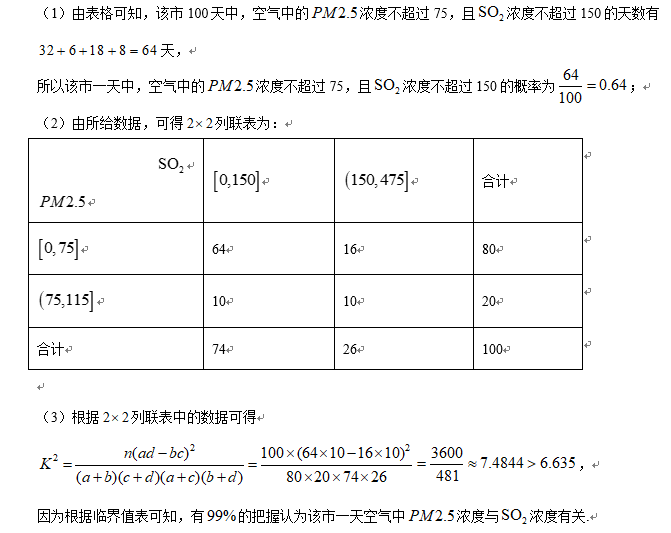
为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了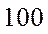
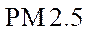
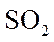
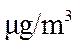
（1）估计事件“该市一天空气中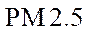
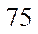
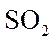
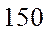
（2）根据所给数据，完成下面的
（3）根据（2）中的列联表，判断是否有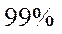
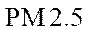
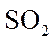
正确答案
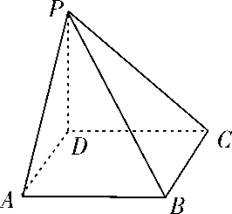
20．（12分）
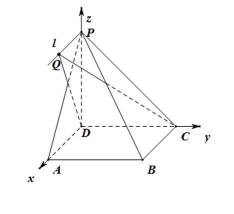
如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．
（1）证明：l⊥平面PDC；
（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．
正确答案
（1）证明：
在正方形
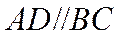
因为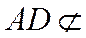
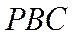
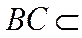
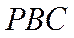
所以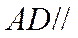
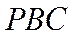
又因为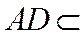
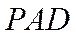
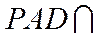
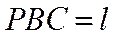
所以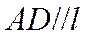
因为在四棱锥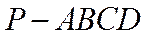
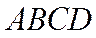
且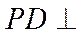
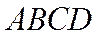
因为
所以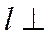
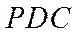
（2）如图建立空间直角坐标系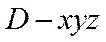
因为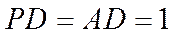
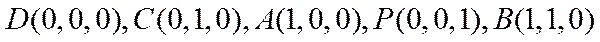
设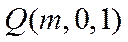
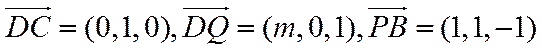
因为QB=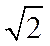
设平面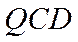
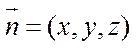
则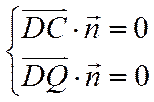
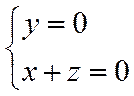
令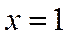
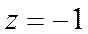
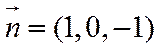
根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线与平面所成角的正弦值等于
所以直线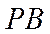
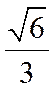
21．（12分）
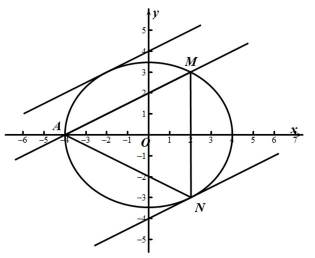
已知椭圆C：
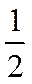
（1）求C的方程；
（2）点N为椭圆上任意一点，求△AMN的面积的最大值.
正确答案
(1)由题意可知直线AM的方程为：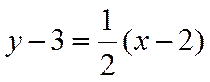
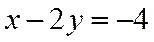
当y=0时，解得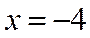
椭圆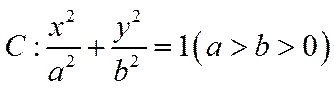
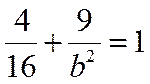
解得b2=12.
所以C的方程：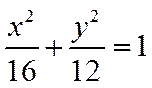
(2)设与直线AM平行的直线方程为：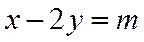
如图所示，当直线与椭圆相切时，与AM距离比较远的直线与椭圆的切点为N，此时△AMN的面积取得最大值.
联立直线方程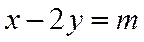
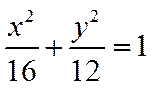
可得：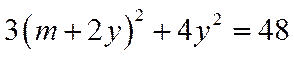
化简可得：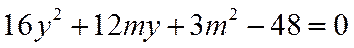
所以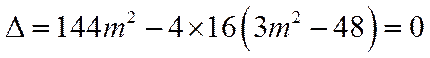
与AM距离比较远的直线方程：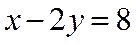
直线AM方程为：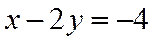
点N到直线AM的距离即两平行线之间的距离，
利用平行线之间的距离公式可得：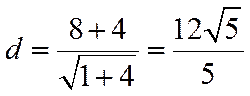
由两点之间距离公式可得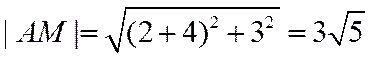
所以△AMN的面积的最大值：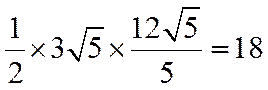
22．（12分）
已知函数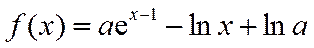
（1）当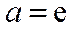
（2）若f（x）≥1，求a的取值范围．
正确答案
（1）
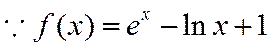
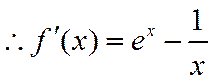
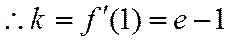
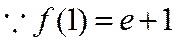
∴函数f(x)在点(1,f(1)处的切线方程为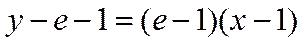
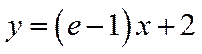
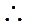
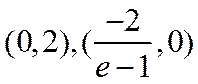
∴所求三角形面积为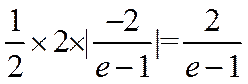
（2）解法一：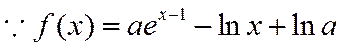
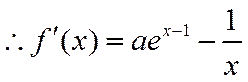
设
∴g(x)在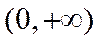
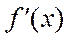
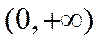
当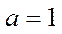
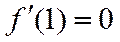
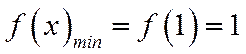
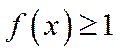
当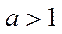
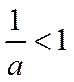
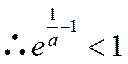
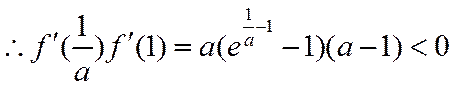
∴存在唯一
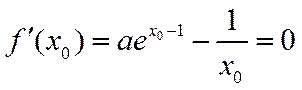
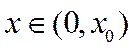
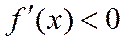
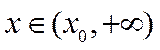
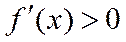
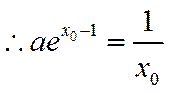
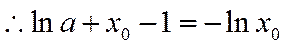
因此
∴
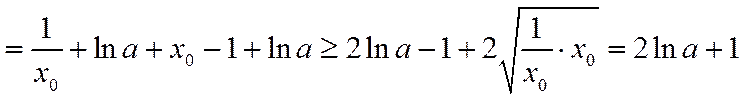
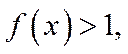
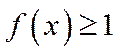
当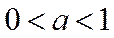
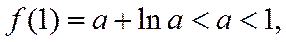
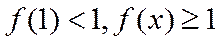
综上所述，实数a的取值范围是[1,+∞).
解法二：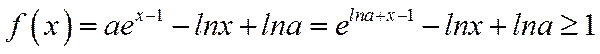
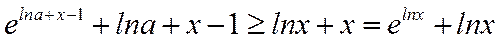
令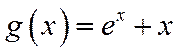
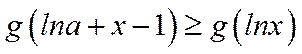
显然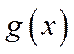
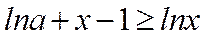
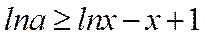
令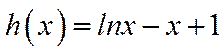
在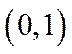
∴
