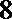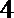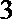1.由


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.在实数的原有运算法则中,我们补充定义新运算“⊙”如下:
当 



当 



则函数 




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.用反证法证明:“方程


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.用反证法证明“如果

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.正方形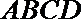
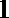
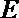
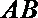
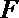
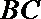
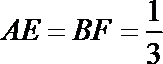
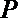
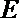
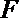
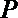
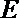
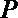
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.下面使用类比推理正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.观察(x2)′=2x,(x4)′=4x3,(cosx)′=-sinx,由归纳推理可得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.用反证法证明命题: “设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.由
①正方形的对角线相等;
②平行四边形的对角线相等;
③正方形是平行四边形,
根据“三段论”推理出一个结论,则这个结论是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知





考察下列结论:
①
②
③数列
④数列
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
14.已知经过计算和验证有下列正确的不等式:




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设等差数列{an}的前n项和为Sn,则S4,S8,S4,S12,S8,S16,S12成等差数列.类比以上结论有:设等比数列{bn}的前n项积为Tn,则T4,_____________,____________,
正确答案


解析
解析已在路上飞奔,马上就到!
知识点
16.平面几何中,△ABC的内角平分线CE分AB所成线段的比
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图(1),在三角形









正确答案
命题是:三棱锥

若

有
证明如下:
在图(2)中,连结

连结
因为

又
于是
解析
解析已在路上飞奔,马上就到!
知识点
18.已知△ABC的三边长为a、b、c,若
正确答案
(用反证法证明1)
∵


∴
∴b2≤ac 即ac-b2≥0.
假设B是钝角,则cosB<0,
由余弦定理可得,

这与cosB<0矛盾,故假设不成立.
∴B不可能是钝角.
(用反证法证明2)
∵


∴
假设B是钝角,则
则B是△ABC的最大内角,所以b>a,b>c,
(在三角形中,大角对大边),
从而

故假设不成立,因此B不可能是钝角.
(用综合法证明)
∵


∴
证明:∵


∴
由余弦定理和基本不等式可得,

∵a,b,c为△ABC三边,∴a+c>b,
∴
∴cosB>0,
∴∠B<900,因此B不可能是钝角.
解析
解析已在路上飞奔,马上就到!
知识点
19.祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家、祖冲之的儿子祖暅首先提出来的. 祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等. 可以用诗句“两个胖子一般高,平行地面刀刀切,刀刀切出等面积,两人必然同样胖”形象表示其内涵. 利用祖暅原理可以推导几何体的体积公式,关键是要构造一个参照体.
试用祖暅原理推导球的体积公式.
正确答案
我们先推导半球的体积. 为了计算半径为R的半球的体积,我们先观察


可以发现





下面进一步验证了猜想的可靠性. 关键是要构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,如右图所示. 下面利用祖暅原理证明猜想.
证明:用平行于平面α的任意一个平面去截这两个几何体,
截面分别为圆面和圆环面.
如果截平面与平面α的距离为
那么圆面半径
圆环面的大圆半径为R,小圆半径为r.
因此

∴ 
根据祖暅原理,这两个几何体的体积相等,
即
所以
解析
解析已在路上飞奔,马上就到!
知识点
20.已知


正确答案
(反证法)假设

设




由上述矛盾可知,
解析
解析已在路上飞奔,马上就到!
知识点
21.已知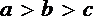
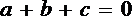
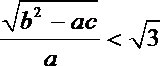
正确答案
因为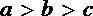
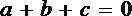
所以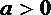
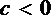
要证明原不等式成立,只需证明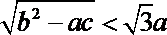
即证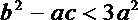
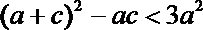
即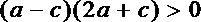
因为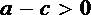
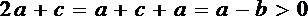
所以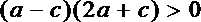
故原不等式成立.
解析
解析已在路上飞奔,马上就到!
知识点
22.求证:
正确答案
同时
于是得
即
解析
解析已在路上飞奔,马上就到!