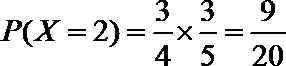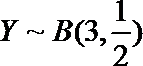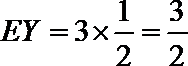数学北碚区2015年高三试卷

精品

单选题
填空题
简答题

立即下载

数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．已知集合，集合，则（）

A（-2，-1）

B[-2，-1]

C[-2，1）

D[-2，-1）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：单选题

分值: 5分

4.曲线在点处切线的斜率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：单选题

分值: 5分

5．阅读下面的程序框图，则输出的（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：单选题

分值: 5分

6．不等式的解集是（）

A[-5，7]

B[-4，6]

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

1．若复数满足则对应的点位于（）

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：单选题

分值: 5分

3. 设函数,则（　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：单选题

分值: 5分

7. 函数存在与直线平行的切线，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

8．过抛物线焦点的直线交抛物线于A,B两点，若，则直线AB的倾斜角为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：单选题

分值: 5分

9．在各项均为正数的等比数列中，若，数列的前项积为，若，则m的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算等比数列的性质及应用

题型：单选题

分值: 5分

10. 某学校4位同学参加数学知识竞赛，竞赛规则规定：每位同学必须从甲、乙两道题中任选一题作答，选甲题答对得30分，答错得－30分；选乙题答对得10分，答错得－10分.若4位同学的总分为0，则这4位同学不同得分情况的种数是（）

A24

B36

C44

D40

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

计数原理的应用

填空题本大题共6小题，每小题5分，共30分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11.已知,,,则_________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

分值: 5分

13. 观察请根据右边所列等式：

①

②

③……，

写出第个等式为_____________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：填空题

分值: 5分

14. 如右图所示，已知C为圆O的直径AB延长线上的一点，割线CE交圆O于D,E两点，连接AD,AE．若圆O的半径为3，BC=4，CD=5，则的大小为_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

与圆有关的比例线段

题型：填空题

分值: 5分

12.关于的不等式的解集为，则不等式的解集为_________

正确答案

（1，2）

解析

解析已在路上飞奔，马上就到！

知识点

分式不等式的解法

题型：填空题

分值: 5分

16. 若不等式对任意实数x恒成立，则实数a的取值

范围是_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题绝对值不等式的解法

题型：填空题

分值: 5分

15. 在直角坐标系X0Y中，以原点O为极点，X轴的正半轴为极轴建立极坐标系. 极坐标方程为的直线与曲线（为参数）相交于A,B两点, 则_______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与圆相交的性质参数方程化成普通方程直线的参数方程圆的参数方程

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 8分

17.等比数列的各项均为正数，且。

（Ⅰ）求数列的通项公式；

（Ⅱ）设，求数列的前项和。

正确答案

解：

（Ⅰ）设数列{an}的公比为q，由得所以。

由条件可知,故。

由得，所以。数列{an}的通项式为an=

（Ⅱ ）

故

所以数列的前n项和为

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项等差数列的判断与证明等差数列的性质及应用等差数列的前n项和及其最值

题型：简答题

分值: 12分

20.把函数的图像向右平移 a()个单位，得到的函数的图像关于直线对称.

（1）求a的最小值；

（2）当a取最小值，求函数在区间上的值域

正确答案

（1）

∴，它关于直线对称，

∴ ∴ ∵

（2）由（1）知

即的值域为

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域正弦函数的对称性函数y=Asin（ωx+φ）的图象变换三角函数中的恒等变换应用

题型：简答题

分值: 13分

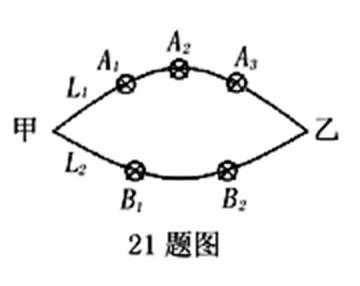
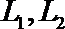
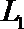
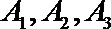
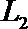
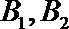
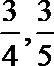
18.如图所示，张先生开车从甲地到乙地有两条路线可走．路线上有三个路口，各路口遇到红灯的概率均为；路线上有两个路口，各路口遇到红灯的概率依次为．

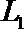
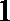
（Ⅰ）若走路线，求最多遇到次红灯的概率；

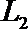
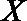
（Ⅱ）若走路线，求遇到红灯次数的数学期望；

（Ⅲ）按照“平均遇到红灯次数最少”的要求，请你帮助张先生从上述两条路线中选择一条最好的上班路线，并说明理由．

正确答案

解:

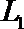
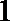
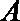
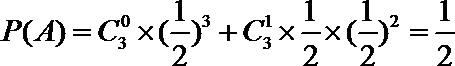
（Ⅰ）设走路线最多遇到次红灯为事件,则

．

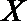
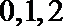
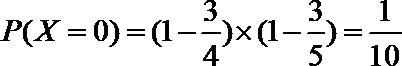
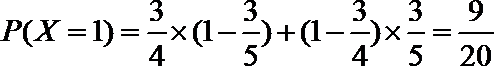
（Ⅱ）依题意，的可能取值为：．

，，

所以随机变量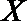的分布列为：

所以．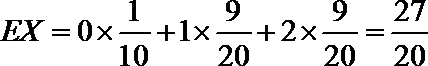

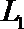
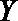
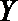
（Ⅲ）设选择路线遇到红灯次数为，则随机变量服从二项分布：

所以

因为，所以选择路线上班最好

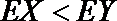
解析

解析已在路上飞奔，马上就到！

知识点

二项分布与n次独立重复试验的模型离散型随机变量及其分布列、均值与方差

题型：简答题

分值: 12分

21．如图，焦距为2的椭圆E的两个顶点分别为和，且与共线．

（Ⅰ）求椭圆E的标准方程；

（Ⅱ）若直线与椭圆E有两个不同的交点P和Q，且原点O总在以PQ为直径的

圆的内部，求实数m的取值范围．

正确答案

解：

（Ⅰ）设椭圆E的标准方程为，由已知得

∴，∵与共线， ∴，又

∴， ∴椭圆E的标准方程为

（Ⅱ）设,把直线方程代入椭圆方程，

消去y，得，,

∴,

（*）

∵原点O总在以PQ为直径的圆内，∴，即

又

由得，依题意且满足（*）

故实数m的取值范围是

解析

解析已在路上飞奔，马上就到！

知识点

平行向量与共线向量向量在几何中的应用椭圆的定义及标准方程圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

题型：简答题

分值: 13分

19.已知.

（Ⅰ）求：过点且与曲线相切的直线方程；

（Ⅱ）对一切恒成立，求实数的取值范围；

正确答案

（Ⅰ）

设切点为，切线的斜率为

∵点在上，∴

∴，解得

∴切线的斜率为，∴切线方程为

（Ⅱ），则，

设，则，

① 单调递减，

② 单调递增，

∴，

∴对一切恒成立的的取值范围是[来源

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 12分

22.已知，函数．

（Ⅰ）当时，讨论函数的单调性；

（Ⅱ）若和是的两个极值点，求证：．

正确答案

解：

（Ⅰ）∵，

，考虑分子

当，即时，

在上，恒成立，此时在上单调递增；

当，即时，方程有两个不相等的实数根．

，，显然，

易知，当或时，；当时，；

∴函数在上单调递减，

在和上单调递增函数

（Ⅱ）∵是的两个极值点，故满足方程，

即是的两个解，∴，

∵

而在中，

因此，要证明，等价于证明

注意到，只需证明，即证

令，则，

当时，，函数在上单调递增；

当时，，函数在上单调递减；

因此，

从而，即，原不等式得证。

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

数学热门试卷