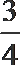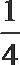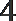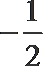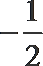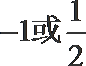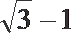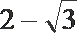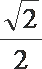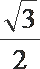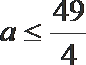5.已知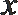
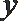

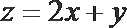
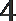
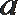
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若正数a,b满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数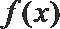

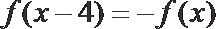
①若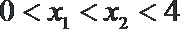

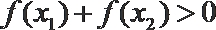
②若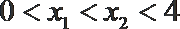
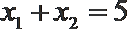
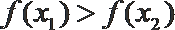
③若方程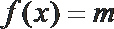
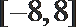
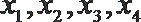
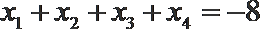
④函数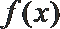
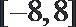
其中结论正确的有 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.实数等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知实数等比数列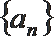

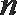
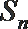
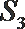
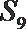
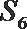
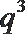
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知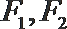
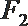
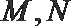
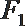
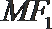
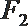
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
正确答案
{-1,1}
解析
解析已在路上飞奔,马上就到!
知识点
12.如图为了测量






正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
13.在△ABC中,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知O是


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数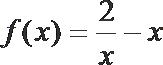
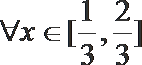
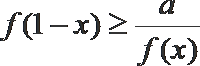
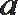
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知正三棱柱






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在







(1)求
(2)若

正确答案
(1)由正弦定理知:

得:
即
(2)由(1)得:
其中,
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列





(1)求数列
(2)当



(3)当



正确答案
(1)当

当


又

即

(2)

(3)
由题设知



(或通过

解析
解析已在路上飞奔,马上就到!
知识点
21.如图,已知圆




(1)求抛物线的方程;
(2)若焦点F在以线段CD为直径的圆E的外部,求m的取值范围.
正确答案
(1)
(2)设


设l的方程为:
于是
即
由

所以
于是
故
又
得到

解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在三棱锥







(1)求证:

(2)若




正确答案
(1)证明:


(2)
连接DC交PE于G,连接FG


又

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)若当


(2)求函数

正确答案
(1)不等式



①当

②当

因为当



所以

综合①②,得所求实数

(2)
当

此时,
当

此时
当

此时
当

此时
综上:
解析
解析已在路上飞奔,马上就到!