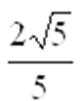1.已知i为虚数单位,则复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.记等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下列结论错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知向量

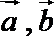
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若最初生产出的溶液含杂质2%,需要进行过滤,且每过滤一次可使杂质含量减少
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,
n维向量可用(x1,x2,x3,x4,…,xn)表示.
设

规定向量


已知n维向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若角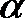
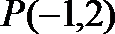
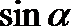
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数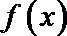

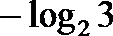
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在四边形ABCD中,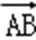
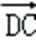
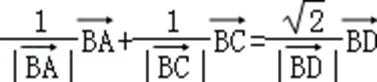
正确答案
25
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(Ⅰ)求
(Ⅱ)若不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知△ABC的角A、B、C所对的边分别是a、b、c,
设向量
(1)若
(2)若




正确答案
证明:(1)∵m∥n
∴asinA=bsinB
即a•

∴a=b ∴△ABC为等腰三角形.
(2)由题意,m•p=0
∴a(b﹣2)+b(a﹣2)=0
∴a+b=ab
由余弦定理4=a2+b2﹣2ab•cos
∴4=a2+b2﹣ab=(a+b)2﹣3ab
∴ab2﹣3ab﹣4=0
∴ab=4或ab=﹣1(舍去)
∴S△ABC=
=

解析
解析已在路上飞奔,马上就到!
知识点
19.设数列



(1)求数列
(2)若




(3)求

正确答案
解:(1)依题意得,
即
当n≥2时,
当n=1时,a1=S1=2
所以
(2)




(3)


(1)—(2),得




解析
解析已在路上飞奔,马上就到!
知识点
20.某书商为提高某套丛书的销量,准备举办一场展销会。据市场调查,当每套丛书售价定为x元时,销售量可达到
假设不计其它成本,即销售每套丛书的利润=售价 一 供货价格。问:
(I)每套丛书定价为100元时,书商能获得的总利润是多少万元?
(Ⅱ)每套丛书定价为多少元时,单套丛书的利润最大?
正确答案
解:(Ⅰ)每套丛书定价为100元时,销售量为15﹣0.1×100=5万套,
此时每套供货价格为
∴书商所获得的总利润为5×(100﹣32)=340万元.
(Ⅱ)每套丛书售价定为x元时,由
依题意,单套丛书利润
∴
∵0<x<150,∴150﹣x>0,
由 
当且仅当
答:(Ⅰ)当每套丛书售价定为100元时,书商能获得总利润为340万元;(Ⅱ)每套丛书售价定为140元时,单套利润取得最大值100元。
解析
解析已在路上飞奔,马上就到!
知识点
22.函数

(1)求a,b的值;
(2)定义:对于连续函数













正确答案
解:(1)求导函数f′(x)=3ax2+b,∵函数f(x)=ax3+bx在点(1,f(1))的切线为方程为3x﹣3y﹣2=0.
∴3a+b=1,a+b=
∴a=
(2)令F(x)=f(x)﹣g(x)=

∴F'(x)=x2﹣x﹣2=(x+1)(x﹣2)
∴当








∴当


∴当



∵当


当


当


当


解析
解析已在路上飞奔,马上就到!
知识点
21.在平面直角坐标系xOy中,已知点A(一1,1),P是动点,且三角形POA的三边所在直线的斜率满足
(I)求点P的轨迹C的方程;
(Ⅱ)若



正确答案
解:(Ⅰ)设点P(x,y)为所求轨迹上的任意一点,
则由kOP+kOA=kPA,
得
整理得轨迹C的方程为y=x2(x≠0且x≠﹣1),
(Ⅱ)(方法一)设
由
故
由O、M、P三点共线可知,

∴
由(Ⅰ)知x1≠0,故y0=x0x1,
同理,由

∴
即(x2+1)[(x0+1)(x2﹣1)﹣(y0﹣1)]=0,
由(Ⅰ)知x2≠﹣1,故(x0+1)(x2﹣1)﹣(y0﹣1)=0,
将y0=x0x1,x2=﹣1﹣x1代入上式得(x0+1)(﹣2﹣x1)﹣(x0x1﹣1)=0,
整理得﹣2x0(x1+1)=x1+1,
由x1≠﹣1得

(方法二)
设
由
故
∴直线OP方程为:y=x1x①;
直线QA的斜率为:
∴直线QA方程为:y﹣1=(﹣x1﹣2)(x+1),
即y=﹣(x1+2)x﹣x1﹣1②;
联立①②,得
∴点M的横坐标为定值
解析
解析已在路上飞奔,马上就到!