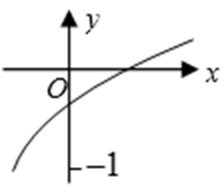
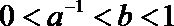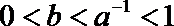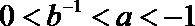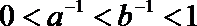1.设全集U=R,集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列命题中,真命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下列关于函数
①
② 

③
④ 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB所围成的弓形面积的2倍,则函数y=f(x)的图象是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数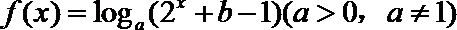
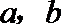
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数



正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
12.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.方程
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
15.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.定义在








其中正确的判断是________(把你认为正确的判断都填上)
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

正确答案


当



当

所以
解析
解析已在路上飞奔,马上就到!
知识点
19.已知

(1)若

(2)若


正确答案
(1) 

(2) 


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)讨论函数
(2)设函数


正确答案
(1)
当





当




即


在
(2)
若函数


解得
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)若不等式



(2)在(1)的条件下, 当

(3)设




正确答案
(1)由已知不等式







(2) 则

当




(3) ∵

∵






∴

解析
解析已在路上飞奔,马上就到!
知识点
22.已知


(1)求
(2)是否存在实数


正确答案
(1)设

故函数
(2)假设存在实数

①当
由于



②当

综上所知,存在实数

解析
解析已在路上飞奔,马上就到!