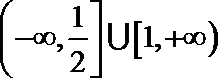1.设集合


正确答案
解析
依题
知识点
6.设



正确答案
解析
若
















知识点
8.设







正确答案
解析
由题意知




知识点
2.下列函数为偶函数的是( )
正确答案
解析
A选项
















知识点
5.已知某一几何体的正视图与侧视图如图所示,则在下列图形中,可以是该几何体的俯视图的图形有( )
正确答案
解析
由正视图和侧视图知:俯视图的图形可以是①②③④,故选A.
知识点
7.已知双曲线






正确答案
解析
根据题意,可知






知识点
3.复数


正确答案
解析
因为



知识点
4.如图,在



正确答案
解析
设方格边长为单位长







知识点
11.设等差数列





正确答案
解析
因为



知识点
9.不等式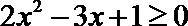
正确答案
解析
由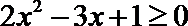
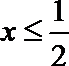
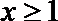

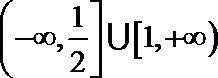
知识点
10.曲线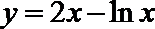
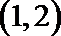
正确答案
解析
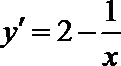
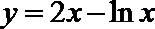
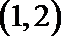
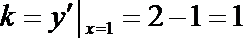
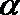
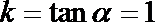
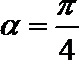
知识点
选做题(第14~15题,只能从中选做一题;两道题都做的,只记第一题的分)
14.(坐标系与参数方程选做题)
曲线




15.(几何证明选讲选做题)
如图,





正确答案
14.
15.
解析
14.曲线






15.因为











知识点
12.执行如图所示的程序框图,则输出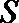
正确答案
解析
此框图所表示的算法功能是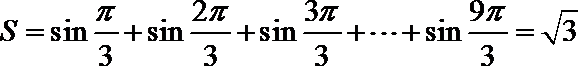
知识点
13.如下图所示,坐标纸上的每个单元格的边长为









按如此规律下去,则
正确答案
解析













知识点
16.已知函数



(1)求函数
(2)在△ABC中,角A、B、C所对的边分别为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某中学一名数学老师对全班



(1)根据以上两个直方图完成下面的
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
附:

(3)若从成绩在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在棱长为2的正方体ABCD-


(1)证明:EF//
(2)证明:
(3)问:线段CD上是否存在一点G,使得直线FG与平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)求a的值;
(2)若对任意的

(3)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列






(1)求数列

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知抛物线C:



(1)求椭圆E的方程;
(2)设直线






正确答案
解析
解析已在路上飞奔,马上就到!