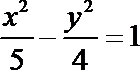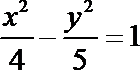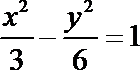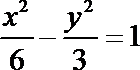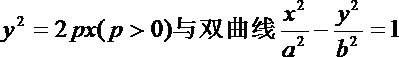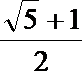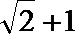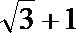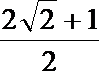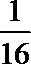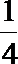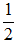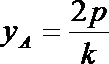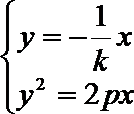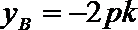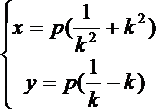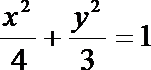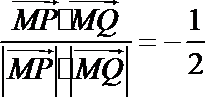4.已知双曲线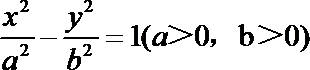
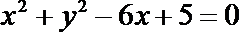
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知抛物线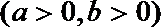

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知曲线C:

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知直线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知点A(3,2),F为抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知正方体










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.直线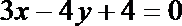
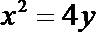
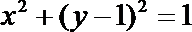
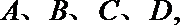
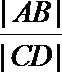
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.椭圆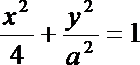
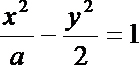
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.抛物线y=ax2(a≠0)的焦点坐标是____________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设m是常数,若点F(0,5)是双曲线
正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
15.过抛物线y2=2px(p>0)的焦点F作直线l,交抛物线于A、B两点,交其准线于C点,若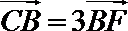
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
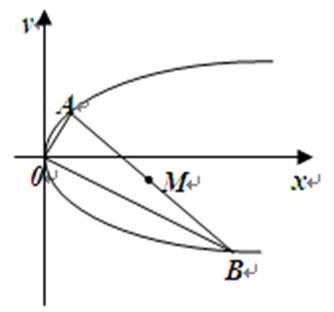
19.如图,过抛物线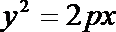

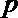
(1)设OA的斜率为k,试用k表示点A、B的坐标;
(2)求弦AB中点M的轨迹方程。
正确答案
(1)∵ 依题意可知直线OA的斜率存在且不为0
∴ 设直线OA的方程为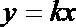
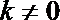
∴ 联立方程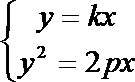
解得 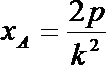
以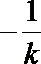
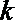
解方程组
解得 
∴ A(
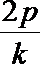
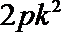
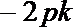
(2)设AB中点M(x,y),
则由中点坐标公式,
得
消去参数k,
得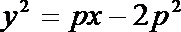
即为M点轨迹的普通方程。
解析
解析已在路上飞奔,马上就到!
知识点
21.设动点




(1)求点
(2)设圆








正确答案
(1)依题意知,
动点



曲线

∵ 
∴ 曲线
(2)设圆的圆心为
∵ 圆

∴ 圆的方程为
令
设圆与

方法1:不妨设

∴
又∵点


∴ 

∴当

方法2:∵
∴
又∵点

∴ 

∴当

解析
解析已在路上飞奔,马上就到!
知识点
17.已知椭圆E:

(1)求椭圆E的方程;
(2)设直线PF2的倾斜角为α,直线PF1的倾斜角为β,当β-α=
正确答案
(1)圆



故


(2)设点P(x,y),因为



设点P(x,y),则



因为β-α=

因为tan(β-α)=
所以
所以点P在定圆x2+y2-2y=3上.
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,过抛物线y2=2px (p>0)焦点F的直线交抛物线于A、B两点,O为坐标原点,l为抛物线的准线,点D在l上。
(1)求证:“如果A、O、D三点共线,则直线DB与x轴平行”;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由。
正确答案
(1)设点A的坐标为(
则直线OA的方程为

抛物线的准线方程是x=-
联立①②,
可得点D的纵坐标为y=-
因为点F的坐标是(
所以直线AF的方程为
y=

其中y
联立y2=2px与④,
可得点B的纵坐标为
y=-
由③⑤可知,DB∥x轴.
当y
(2)逆命题:如果DB与x轴平行,
则A、O、D三点共线它是真命题,证明如下
因为抛物线y2=2px(p>0)的焦点为F(
所以经过点F的直线AB的方程可设为x=my+
代入抛物线方程,得y2-2pmy-p2=0.
若记A(x1,y1),B(x2,y2),
则y1,y2是该方程的两个根,所以y1y2=-p2.
因为DB∥x轴,且点D在准线x=-
所以点D的坐标为(-
故直线DO的斜率为k=
即k也是直线OA的斜率,
所以直线AD经过原点O,
即A、O、D三点共线.
解析
解析已在路上飞奔,马上就到!
知识点
20.矩形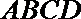
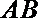
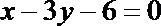
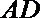
(1)求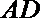
(2)求矩形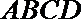
(3)若动圆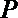
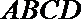
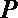
正确答案
(1)因为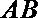

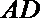
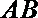
所以直线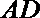
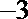
又因为点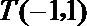
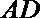
所以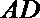
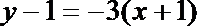
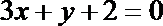
(2)由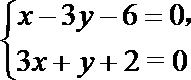
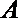
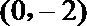
因为矩形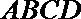
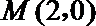
所以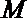
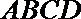
又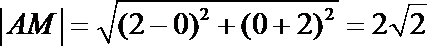
从而矩形
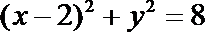
(3)因为动圆
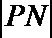
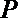
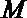
所以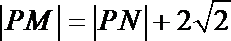
即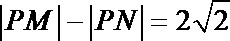
故点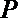
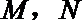
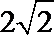
因为实半轴长
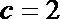
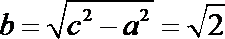
从而动圆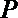
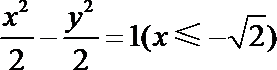
解析
解析已在路上飞奔,马上就到!
知识点
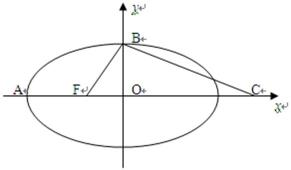
22.如图,F是椭圆

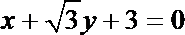
(1)求椭圆的方程:
(2)过点A的直线l2与圆M交于PQ两点,且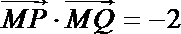
正确答案
(1)F(-c,0),B(0,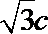
∵ kBF=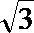
kBC=-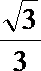
C(3c,0)
且圆M的方程为(x-c)2+y2=4c2,
圆M与直线l1:x+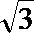
∴ 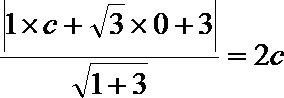
解得c=1,
∴ 所求的椭圆方程为
(2) 点A的坐标为(-2,0),
圆M的方程为(x-1)2+y2=4,
过点A斜率不存在的直线与圆不相交,
设直线l2的方程为y=k(x+2),
∵ 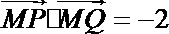
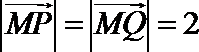
∴ cos<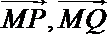
∴ ∠PMQ=120°,
圆心M到直线l2的距离d=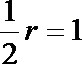
所以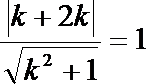
∴ k=
所求直线的方程为x±2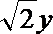
解析
解析已在路上飞奔,马上就到!