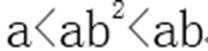数学浦东新区2012年高三试卷

精品

填空题
单选题
简答题

立即下载

数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、单选题

3、简答题

真题试卷
模拟试卷

填空题本大题共12小题，每小题5分，共60分。把答案填写在题中横线上。

题型：填空题

分值: 5分

5．不等式的解为________．

正确答案

（-∞，0）∪（1，+∞）

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

9．甲、乙两人同时同地沿同一路线走到同一地点。甲有一半时间以速度a行走，另一半时间以速度b行走，乙有一半路程以速度a行走，另一半路程以速度b行走。如果，则两人先到达指定地点的是________．

正确答案

甲

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：填空题

分值: 5分

10．若正数满足，则的取值范围是________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 5分

1．设，，则三者的大小关系是________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 5分

2．集合A=，集合B=，则________．

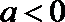
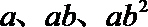
正确答案

（-2，-1]

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 5分

3．如果－＜b＜a＜，则2b－a的取值范围是________．

正确答案

（，）

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 5分

4．若不等式的解集为，则 ________．

正确答案

—1

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 5分

6．已知全集I=R，集合，，则B中所有元素的和是________．

正确答案

2007 或2006 或－2

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：填空题

分值: 5分

7．如果函数在区间上有意义，那么实数a的取值范围是________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 5分

8．关于的方程有负实数根的充要条件是________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 5分

11．“不等式组成立”是 “不等式组成立”__________条件．

正确答案

必要非充分

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：填空题

分值: 5分

12.设N=2n（n∈N*，n≥2），将N个数x1，x2，…，xN依次放入编号为1，2，…，N的N个位置，得到排列P0=x1x2…xN．将该排列中分别位于奇数与偶数位置的数取出，并按原顺序依次放入对应的前和后个位置，得到排列P1=x1x3…xN-1x2x4…xN，将此操作称为C变换，将P1分成两段，每段个数，并对每段作C变换，得到；当2≤i≤n-2时，将Pi分成2i段，每段个数，并对每段C变换，得到Pi+1，例如，当N=8时，P2=x1x5x3x7x2x6x4x8，此时x7位于P2中的第4个位置．

（1）当N=16时，x7位于P2中的第___个位置；

（2）当N=2n（n≥8）时，x173位于P4中的第___个位置。

正确答案

（1）6

（2）

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

单选题本大题共4小题，每小题5分，共20分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

13．“”是的（）

A充分非必要条件

B必要非充分条件

C充要条件

D既非充分又非必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

14．若集合中三个元素为边可构成一个三角形，那么该三角形一定不可能是（）

A锐角三角形

B直角三角形

C钝角三角形

D等腰三角形

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：单选题

分值: 5分

16．已知函数（为常数，且），对于定义域内的任意两个实数、，恒有成立，则正整数可以取的值有（）

A4个

B5个

C6 个

D7个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

15．正方形的边长为，点在边上，点在边上，。动点从出发沿直线向运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点第一次碰到时，与正方形的边碰撞的次数为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 14分

20．已知：，

（1）当时，恒有，求的取值范围；

（2）当时，恒有，求的取值范围；

（3）当时，恰有成立，求的值。

正确答案

（1）或

∴ 。

（2），成立

对称轴

（3）

∵时

恰有成立

∴ 。

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 12分

17．设集合函数的定义域为，集合为函数（）的值域，集合为不等式的解集．

（1）求；

（2）若，求的取值范围．

正确答案

（1），，

（2），a=0时，，满足

时，，不满足时，，满足

时，若满足，则故有

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 14分

18．设全集，关于的不等式（）的解集为．

（1）分别求出当和时的集合；

（2）设集合，若中有且只有三个元素，求实数的取值范围．

正确答案

（1）当时，；当时，．

（2）由可以得到：．

当时，解集是；当时，解集是．

（i）当时，，不合题意；

（ii）当时，

因为

所以，得，即，所以．

由有3个元素，则必须满足

所以．

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 14分

19．解关于的不等式：

正确答案

时，原不等式的解集是，

时，原不等式的解集是

时，原不等式的解集是，时，原不等式的解集是

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：简答题

分值: 16分

21．设集合P=

（1）试判断；，是否属于集合P？

（2）若属于P，试寻找其充要条件．

（3）根据对第（1），（2）小题的研究，请你对属于集合P的函数从函数性质方面提出一个有价值的结论，说明理由;若，利用研究所得的结论判断与集合P的关系。

正确答案

（1） f1（x）不属于P; f2（x）∈P

（2） b=0

（3） f（x）为奇函数，且f（x）不属于P

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

数学热门试卷