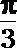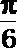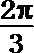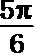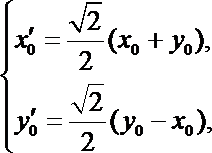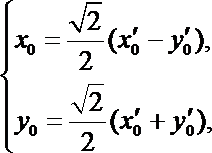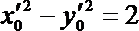5.不等式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.直线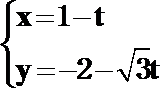
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若点P(3,m)在以点F为焦点的抛物线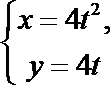
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
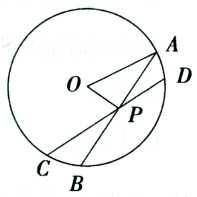
2.如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线分别与AE、BE相交于C、D,若∠AEB=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.关于x的不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.柱坐标(2,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.极坐标方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若关于


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图所示,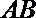
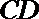

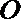
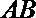
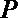
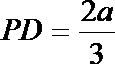
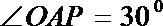
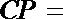
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.求曲线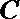
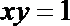
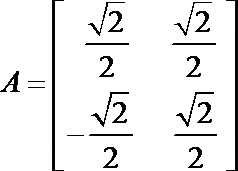
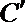
正确答案
设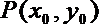
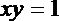
在矩阵A变换下得到另一点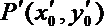
则有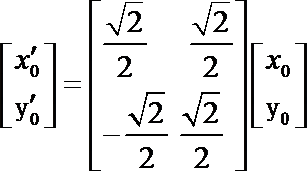
即
所以
又因为点P在曲线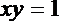
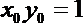
故有
即所得曲线方程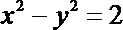
解析
解析已在路上飞奔,马上就到!
知识点
21.直线



正确答案
解法1:设
则直线




代入
得
与
解法2:设

直线



则有
代入
再设直线




代入
得
与
解析
解析已在路上飞奔,马上就到!
知识点
22.证明不等式:
正确答案
即
又

即
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,圆




圆





求证:
正确答案
连结AO1,并延长分别交两圆于点E和点D连结BD、CE,
因为圆O1与圆O2内切于点A,所以点O2在AD上,
故AD,AE分别为圆O1,圆O2的直径。
从而
于是
所以AB:AC为定值。
解析
解析已在路上飞奔,马上就到!
知识点
20.已知△ABC,A(-1,0),B(3,0),C(2,1),对它先作关于x轴的反射变换,再将所得图形绕原点逆时针旋转90°.
(1)分别求两次变换所对应的矩阵M1,M2;
(2)求点C在两次连续的变换作用下所得到的点的坐标.
正确答案
(1)M1=

(2)因为M=M2 M1=
所以M
故点C在两次连续的变换作用下所得到的点的坐标是(1,2).
解析
解析已在路上飞奔,马上就到!
知识点
18.在直角坐标系中,曲线C:
(1)将直线l的极坐标方程化为直角坐标方程;
(2)设点P在曲线C上,求P点到直线l的距离的最大值.
正确答案
(1)直线的直角坐标方程为4x-3y-12=0
(2)当cos(
解析
解析已在路上飞奔,马上就到!