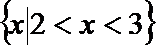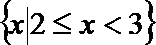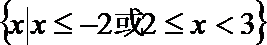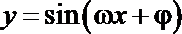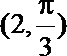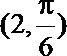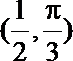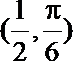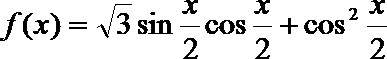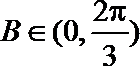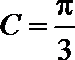2.


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
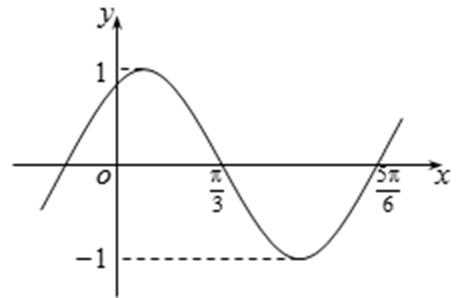
5.已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知非零向量






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合
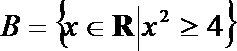
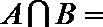
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数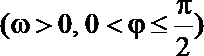
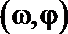
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若下边的程序框图输出的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,双曲线的中心在坐标原点







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设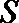
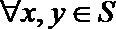
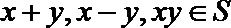
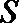
①实数集是封闭集;
②全体虚数组成的集合是封闭集;
③封闭集一定是无限集;
④若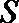
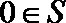
⑤若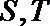
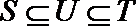
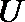
其中真命题是( ).
正确答案
①,④
解析
解析已在路上飞奔,马上就到!
知识点
13. 如下图,在圆内接四边形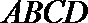
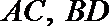
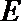
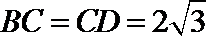
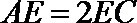
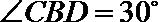
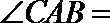
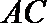
正确答案
30;6
解析
解析已在路上飞奔,马上就到!
知识点
12. 设



正确答案
7;6
解析
解析已在路上飞奔,马上就到!
知识点
10. 
正确答案
-160
解析
解析已在路上飞奔,马上就到!
知识点
9.若复数

正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
11

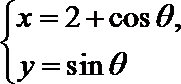
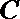
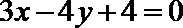
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
15. 在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2-a2=bc.
(Ⅰ)求角A的大小;
(Ⅱ)设函数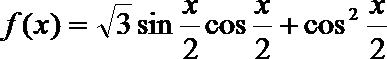
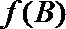

(Ⅲ)求函数的最小正周期和最大值及最小值.
正确答案
(Ⅰ)在△ABC中,因为b2+c2-a2=bc,
由余弦定理 a2= b2+c2-2bccosA 可得cosA=
∵ 0<A<π ,
∴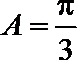
(Ⅱ)(Ⅲ)
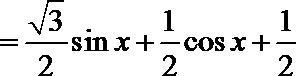
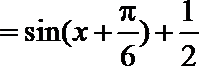
∵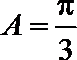
∴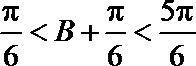
∴当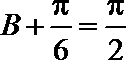
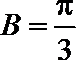
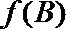

又∵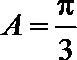
∴△ABC为等边三角形.
解析
解析已在路上飞奔,马上就到!
知识点
17. 甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为

(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;
(Ⅱ)求
(Ⅲ)设甲、乙、丙三人中破译出密码的人数为


正确答案
解:记“甲、乙、丙三人各自破译出密码”分别为事件
依题意有

(Ⅰ)甲、乙二人中至少有一人破译出密码的概率为

(Ⅱ)设“三人中只有甲破译出密码”为事件


所以

(Ⅲ)

所以






所以,
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数
(Ⅰ)若曲线



(Ⅱ)若对于


(Ⅲ)记




正确答案
(I)直线
函数

因为


所以

由



所以


(II) 
由



所以


所以当


因为对于

所以
则


所以

(III)依题得

由



所以函数


又因为函数

解得
所以

解析
解析已在路上飞奔,马上就到!
知识点
19. 已知椭圆








(Ⅰ)求椭圆的方程;
(Ⅱ)求
(Ⅲ)试用

正确答案
(Ⅰ)依题意可得,

又


(Ⅱ)设直线

由

设


可得
设线段



由题意有

可得


(Ⅲ)设椭圆上焦点为
则

由


又

所以△


设

可知


所以,当


所以,当


解析
解析已在路上飞奔,马上就到!
知识点
20. 将



定义

(Ⅰ)当

(Ⅱ)当

(Ⅲ)当

正确答案
(Ⅰ)












(Ⅱ)
上式转化为
在上述





所以


若使
所以

所对应的一个排列为:
(Ⅲ)不可以.
例如排列


所以只能将排列

对于排列


如此不断循环下去,不可能经过有限次调整使其波动强度降为
解析
解析已在路上飞奔,马上就到!
知识点
16. 如图, 








(Ⅰ)求证:

(Ⅱ)求二面角
(Ⅲ)设点




正确答案
(Ⅰ)证明: 因为



因为
所以
从而

(Ⅱ)解:因为
所以建立空间直角坐标系
因为



所以
由


则




所以

设平面



令

因为




所以
因为二面角为锐角,所以二面角

(Ⅲ)解:点


则
因为

所以
即

此时,点


解析
解析已在路上飞奔,马上就到!