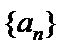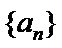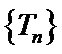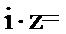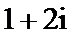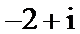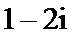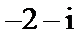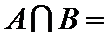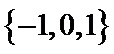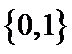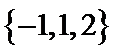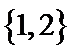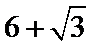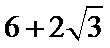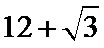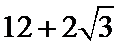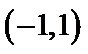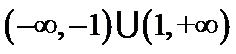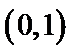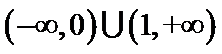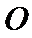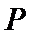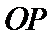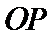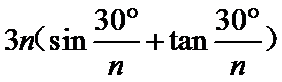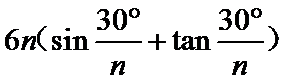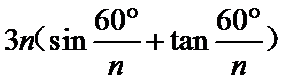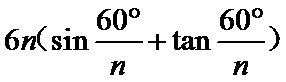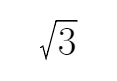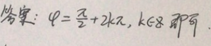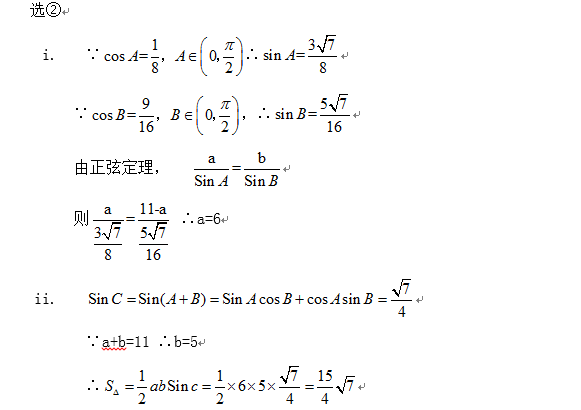3．在
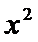
正确答案
5．已知半径为1的圆经过点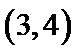
正确答案
8．在等差数列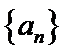
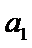
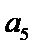
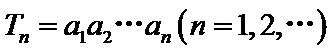
正确答案
2．在复平面内，复数z对应的点的坐标是（1,2），则
A
B
C
D
正确答案
1．已知集合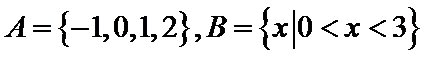
A
B
C
D
正确答案
4．某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为
A
B
C
D
正确答案
6．已知函数
A
B
C
D
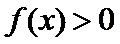
正确答案
7．设抛物线的顶点为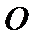
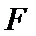
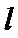
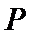
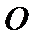
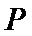
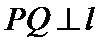
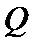
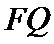
A经过点
B经过点
C平行于直线
D垂直于直线
正确答案
9．已知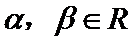
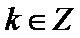
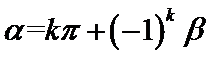
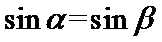
正确答案
10．2020年3月14日是全球首个国际圆周率日（π Day）.历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似，数学家阿尔·卡西的方法是:当正整数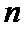
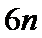
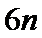
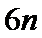
A
B
C
D
正确答案
13．已知正方形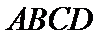
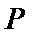
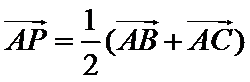
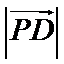
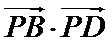
正确答案
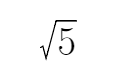
15．为满足人民对美好生活的向往，环保部门要求企业加强污水治理，排放未达标的企业要限期整改，设企业的污水排放量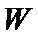
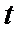
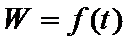
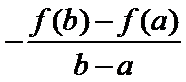
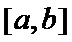
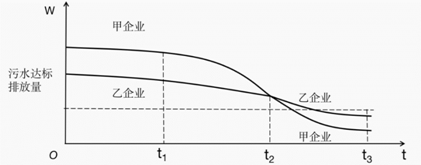
① 在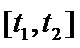
② 在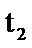
③ 在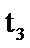
④ 甲企业在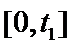
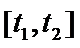
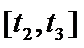
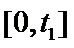
其中所有正确结论的序号是______.
正确答案
①②③
11．函数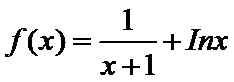
正确答案
{x|x>0}
12．已知双曲线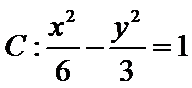
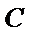
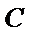
正确答案
（3,0），
14．若函数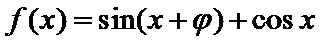
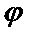
正确答案
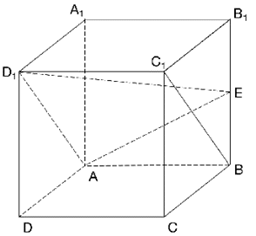
16．(本小题13分)
如图，在正方体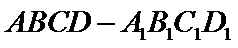
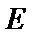
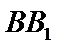
(Ⅰ)求证: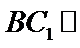 
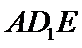
(Ⅱ)求直线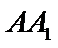
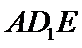
正确答案
19．（本小题15分）
已知函数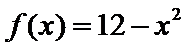
（Ⅰ）求曲线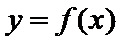
（Ⅱ）设曲线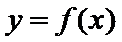
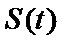
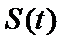
正确答案
20．（本小题15分）
已知椭圆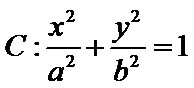
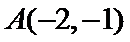
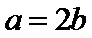
（Ⅰ）求椭圆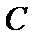
（Ⅱ）过点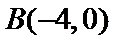
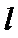
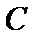
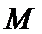
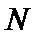
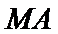
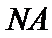
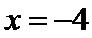
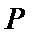
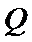
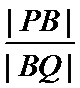
正确答案
17．(本小题13分)
在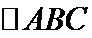
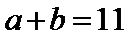
(I) a的值；
(II)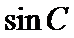 
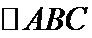
条件①: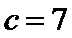 
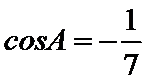
条件②: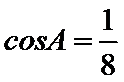 
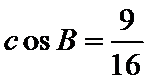
注:如果选择条件①和条件②分别解答，按第一个解答计分。
正确答案
18.（本小题14分）
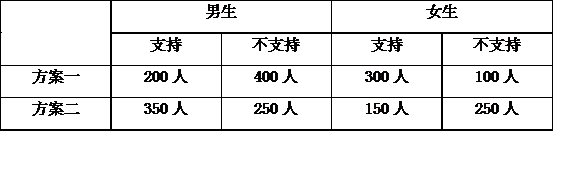
某校为举办甲、乙两项不同活动，分别设计了相应的活动方案：方案一、方案二。为了解该校学生对活动方案是否支持，对学生进行简单随机抽样，获得数据如下表：
假设所有学生对活动方案是否支持相互独立。
（Ⅰ）分别估计该校男生支持方案一的概率、该校女生支持方案一的概率；
（Ⅱ）从该校全体男生中随机抽取2人，全体女生中随机抽取1人，估计这3人中恰有2人支持方案一的概率；
（Ⅲ）将该校学生支持方案二的概率估计值记为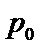
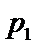
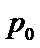
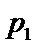
正确答案
21.（本小题15分）
已知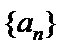
①对于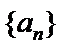
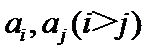
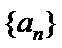
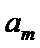
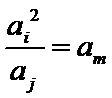
②对于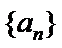
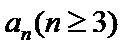
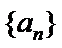
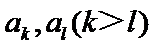
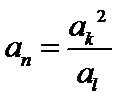
（Ⅰ）若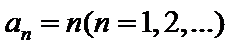
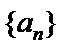
（Ⅱ）若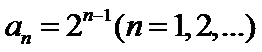
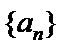
（Ⅲ）若
