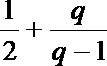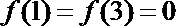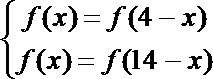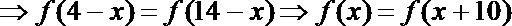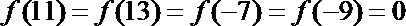3.函数
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
9.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
4.某学校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设, 其中甲同学必须被选派的概率是______
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.将7名学生分配到甲、乙两个宿舍中, 每个宿舍至少安排2名学生, 那么互不相同的分配方案共有________种
正确答案
112
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.不等式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
π
解析
解析已在路上飞奔,马上就到!
知识点
7.已知等差数列{an}前n项和为Sn。 若m>1, m∈N且

正确答案
10
解析
解析已在路上飞奔,马上就到!
知识点
10.已知等差数列{an}公差不为0, 其前n项和为Sn, 等比数列{bn}前n项和为Bn, 公比为q, 且|q|>1, 则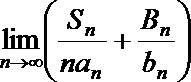
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
(1)
(2)
(3)
(4)
其中正确的命题序号为______________(写出所有正确命题序号)
正确答案
(2),(3),(4)
解析
解析已在路上飞奔,马上就到!
知识点
12.已知n次多项式









正确答案

解析
解析已在路上飞奔,马上就到!
知识点
14.设数列{an}前n项和
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.2002年8月在北京召开了国际数学家大会, 会标如图示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形, 若直角三角形中较小的锐角为θ,大正方形面积是1, 小正方形面积是

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设[x]表示不超过x的最大整数(例如:[5.5]=5,[一5.5]=-6),则不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数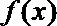
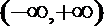

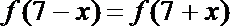
(1)试判断函数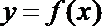
(2)试求方程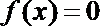
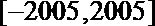
正确答案
(1)由
∵在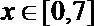
∴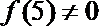
故
(2)由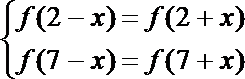
∴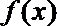
∴
∴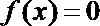
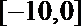
从而方程在

在[2000, 2005]上有2个根.
故方程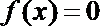
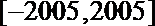
解析
解析已在路上飞奔,马上就到!
知识点
17.设复数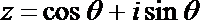
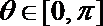
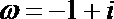

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.命题甲: 

命题乙: 

正确答案
当甲真时,设

则
当乙真时,

则
∴当甲乙有但仅有一个为真命题时,即
∴
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,一个水轮的半径为4 m,水轮圆心O距离水面2 m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间。
(1)将点p距离水面的高度z(m)表示为时间t(s)的函数;
(2)点p第一次到达最高点大约需要多少时间?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.
64个正数排成8行8列, 如上图所示:在符合



(1)若


(2)记第n行各项之和为An(1≤n≤8),数列{an}、{bn}、{cn}满足




(3)对(2)中的



正确答案
(1)∵
∴
∵
∴
(2)设第一行公差为d,
解出:

∵
∴
∴
∵
∴
而
∴
∴
故
∵
∴
∴
(3)∵
∴
∴
解出:6.643<n≤7.643
∵
∴n=7,即
解析
解析已在路上飞奔,马上就到!
知识点
19.已知△ABC中,

正确答案
得
∴


则
由
即
∴


则所求的角


解析
解析已在路上飞奔,马上就到!