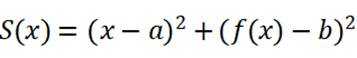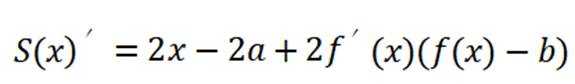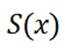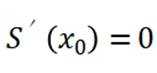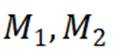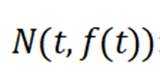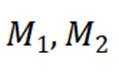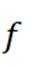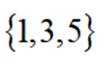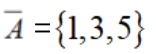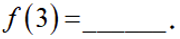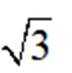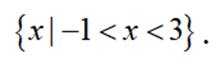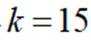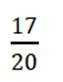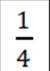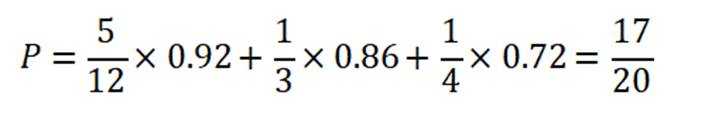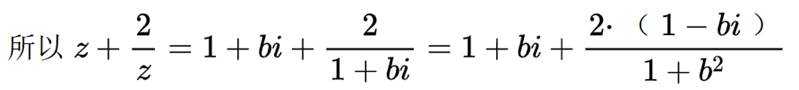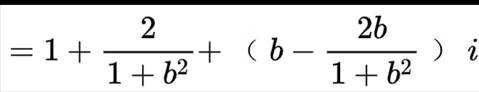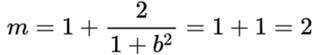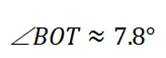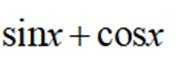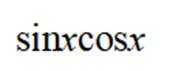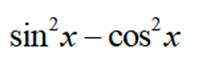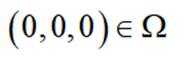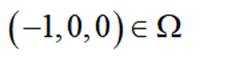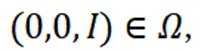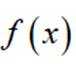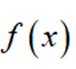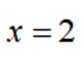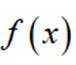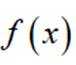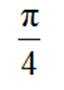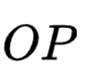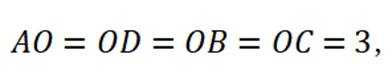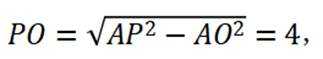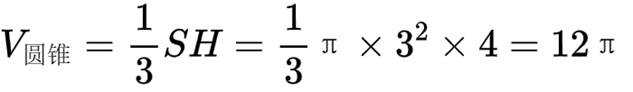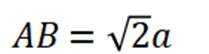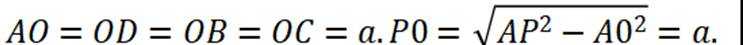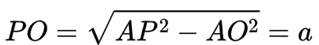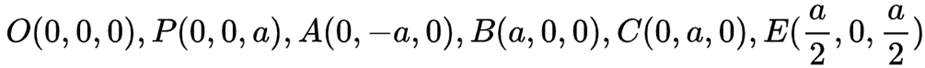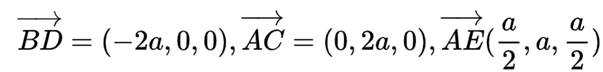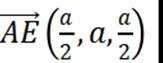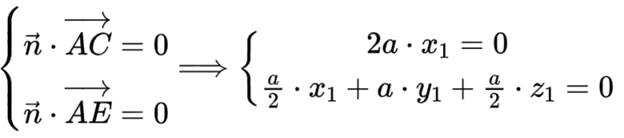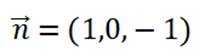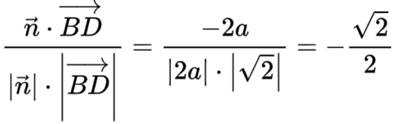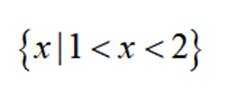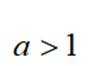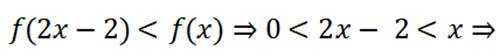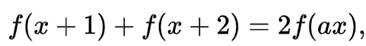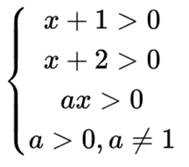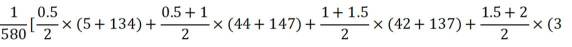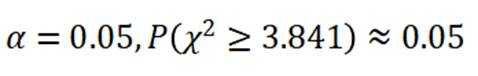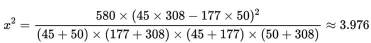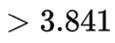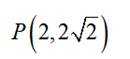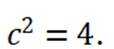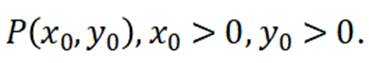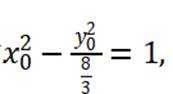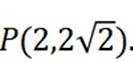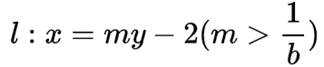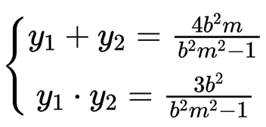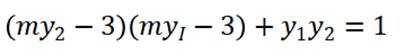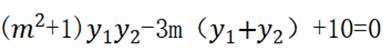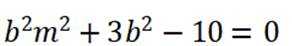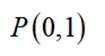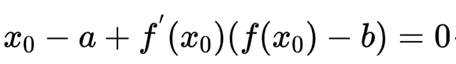设全集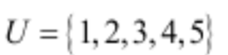
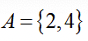
正确答案
解析
本题主要考察了补集的概念。
两个集合联立可得
已知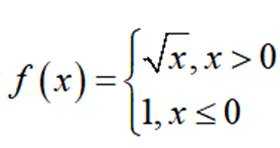
正确答案
解析
本题主要考察了分段函数的知识点。
将3代入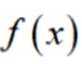
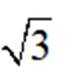
已知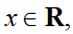
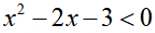
正确答案
解析
本题主要考察了一元二次不等式的求解。
方程
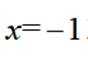
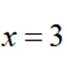
故不等式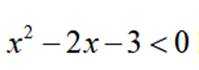
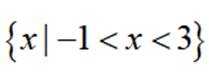
故答案为:
已知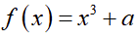
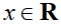
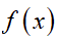
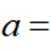
正确答案
0
解析
本题主要考察了奇函数的性质。
由题可知,F(0)=0,则a=0
故答案为:0.
已知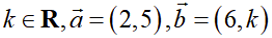

正确答案
15
解析
本题主要考察了平面向量平行的性质。
根据向量平行的坐标表示得到方程,解出即可.
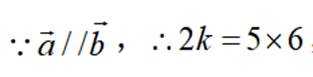
故答案为:15.
在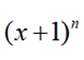
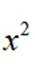
正确答案
10
解析
本题主要考察了二项式定理的知识点。
由题可知,展开式中各项系数的和是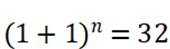
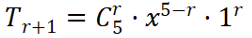
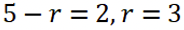
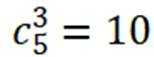
已知抛物线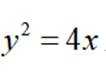
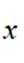
正确答案
解析
本题主要考察了抛物线的定义以及抛物线方程的应用。
设P坐标为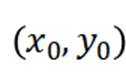

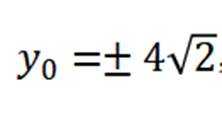
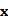
某校举办科学竞技比赛,有
正确答案
解析
本题主要考察了全概率公式的应用。
由题可知,A题库占比为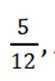
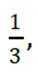
已知虚数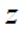
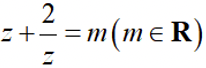

正确答案
2
解析
本题主要考察了复数的概念以及复数的运算。其中涉及到虚数的实部、复数的加、除法运算,还有根据复数为实数的条件来求解参数等知识点。
设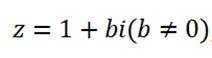
因为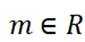
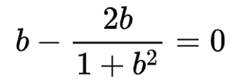
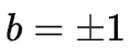
设集合A中的元素皆为无重复数字的三位正整数,且元素中任意两者之积皆为偶数,求集合中元素个数的最大值______.
正确答案
329
解析
本题主要考察了排列组合以及集合的性质这两个知识点。
由题可知,集合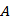
(1)若个位为0,这样的偶数有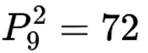
(2)若个位不为0,这样的偶数有
所以集合元索个数最大值为256+72+1=329种.
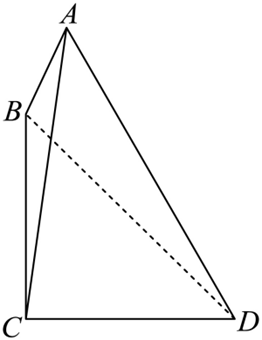
已知点B在点C正北方向,点D在点C的正东方向,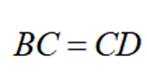
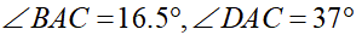
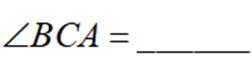
正确答案
解析
本题主要考察了三角形的内角定理、外角性质以及特殊角的三角函数等知识点。
不妨设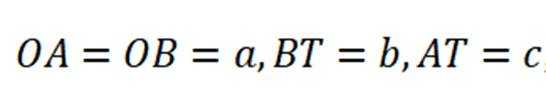
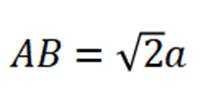
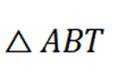
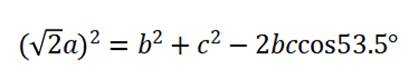
在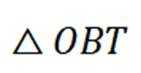

在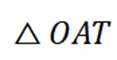
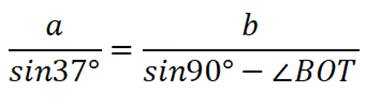
①②③联立
无穷等比数列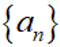
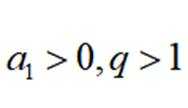
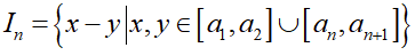
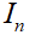
正确答案
解析
本题主要考察了无穷等比数列的性质、集合的概念以及区间的相关知识。
由题不妨设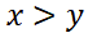
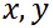
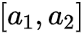
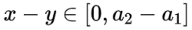
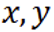

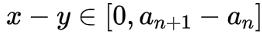
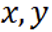

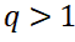
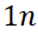
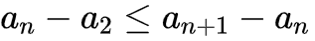
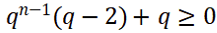
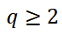
已知气候温度和海水表层温度相关,且相关系数为正数,对此描述正确的是()
正确答案
解析
本题主要考察了相关系数的意义以及对数据变化趋势的理解。通过相关系数的正负来判断两个变量之间变化趋势的一致性或相反性。同时也涉及到对气候温度和海水表层温度关系的分析推理能力。
对于AB,当气候温度高,海水表层温度变高变低不确定,故AB错误.
对于CD,因为相关系数为正,故随着气候温度由低到高时,海水表层温度呈上升趋势,
故C正确,D错误.
故选:C.
下列函数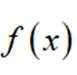
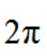
正确答案
解析
本题主要考察了三角函数的化简、三角函数的周期性这些知识点。
对于A,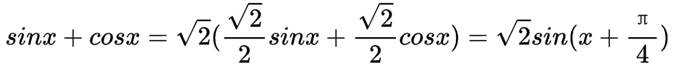
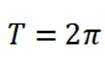
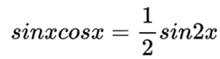

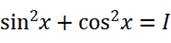
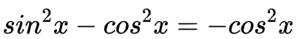
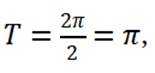
定义一个集合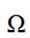
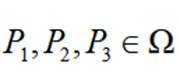

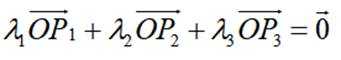
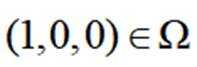
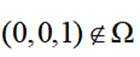
正确答案
解析
本题主要考察了空间向量以及集合的相关知识点。
因为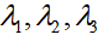
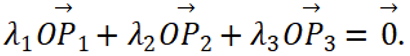
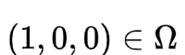
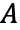

对于B,若(1,0,0),(-1,0,0)均属于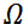
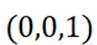
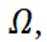
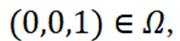
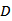
故D错误,故答案选C.
已知函数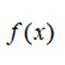
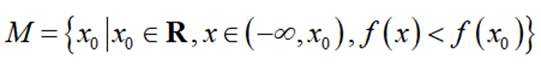
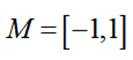

正确答案
解析
本题主要考察了函数的定义域、单调性、奇偶性、极值以及最值等知识点。同时还需要对集合的概念有深入理解,通过集合来描述函数的一些性质。
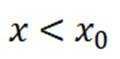
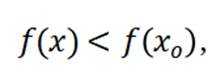
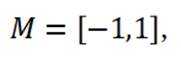
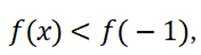
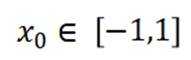
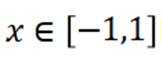

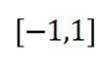
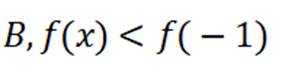
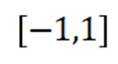
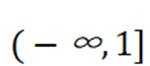
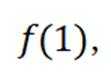
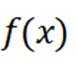

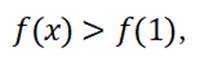
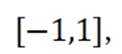
对于C,在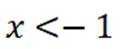
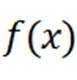
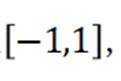
对于D,因为当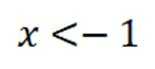
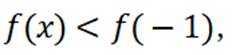
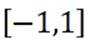
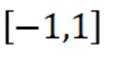
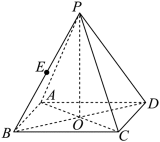
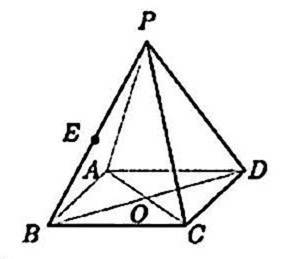
如图为正四棱锥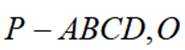
(1)若
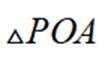
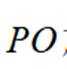
(2)若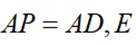
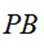
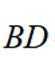
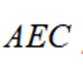
正确答案
(1)
(2)
解析
本题主要考察了正四棱锥的性质、圆锥的体积计算、空间直角坐标系的建立、利用空间向量求线面角等知识点。
(1)因为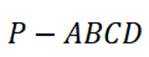
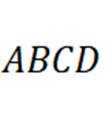
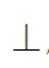
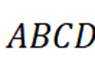
因为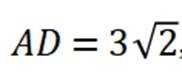
因为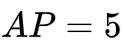
所以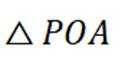
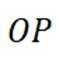
所以
(2)如图建立空间直角坐标,因为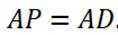
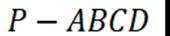
则
则可得
故
设
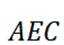
令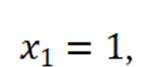
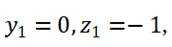
则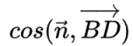
设直线BD与平面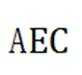
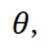
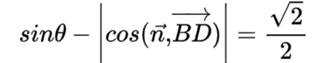
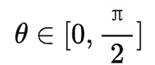
所以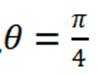
若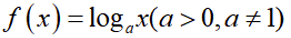
(1)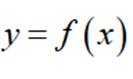
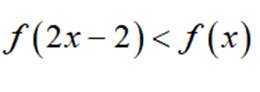
(2)存在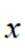
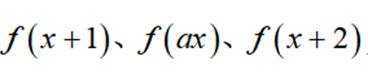
正确答案
(1)
(2)
解析
本题主要考察了对数函数的性质,包括对数函数过定点、单调性,以及等差数列的概念,还有方程有解问题等知识点。
(1)由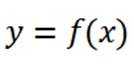
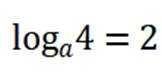
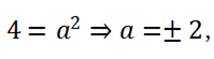
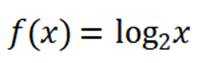
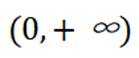
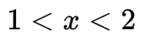
(2)因为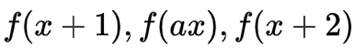
即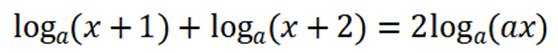
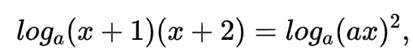

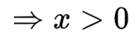
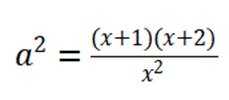
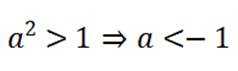
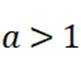
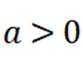
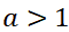
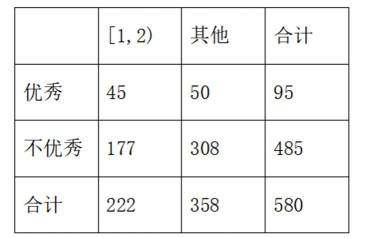
为了解某地初中学生体育锻炼时长与学业成绩的关系,从该地区29000名学生中抽取580人,得到日均体育锻炼时长与学业成绩的数据如下表所示:
(1)该地区29000名学生中体育锻炼时长不少于1小时人数约为多少?
(2)估计该地区初中学生日均体育锻炼的时长(精确到0.1)
(3)是否有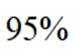
(附: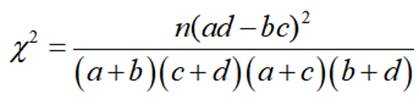
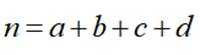
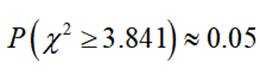
正确答案
(1)12500
(2)0.9h
(3)学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关。
解析
题主要考察了统计相关的知识点,包括通过样本数据计算比例来估计总体情况;计算样本的平均值来估计总体的平均时长;以及通过独立性检验来判断两个变量之间是否有关联。
(1)580人中体育锻炼时长不小于1小时人数占比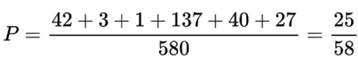
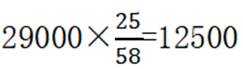
(2)
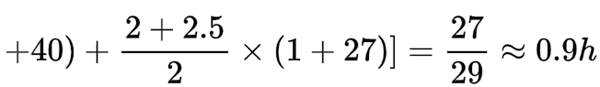
(3)
①提出原假设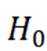
②确定显著性水平
③
④否定原假设,即学业成绩优秀与日均体育锻炼时长不小于1小时但小于2小时有关。
已知双曲线
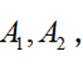

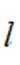
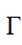

(1)若离心率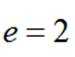
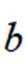
(2)若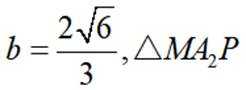
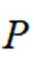
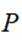
(3)连接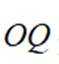
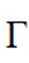
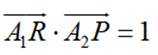
正确答案
(1)
(2)
(3)
解析
本题主要考察了双曲线的性质,如离心率、顶点坐标等,还涉及到直线与双曲线的位置关系,以及等腰三角形的性质、向量的数量积等知识点。
(1)因为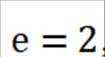

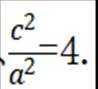
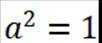
因为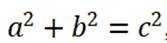
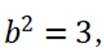
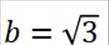
(2)因为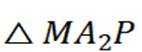
①若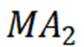
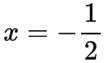
②若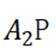
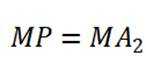
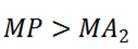
③若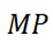
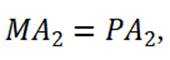
则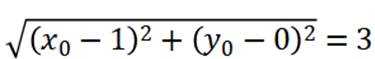
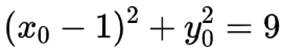
得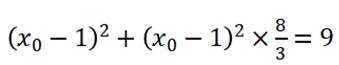
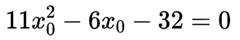
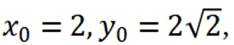
(3)由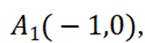

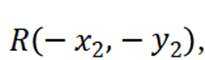
联立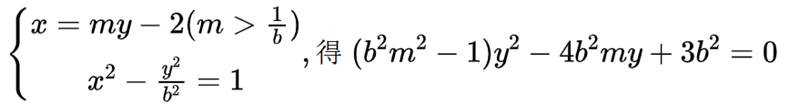

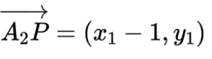
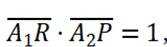

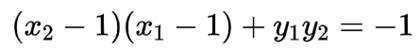
化简后可得到
再由韦达定理得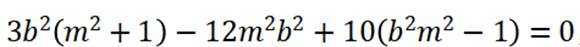
所以
对于一个函数

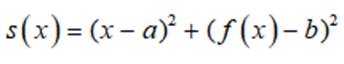

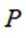
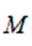
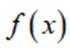
(1)对于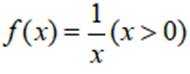
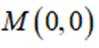
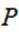
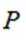
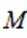
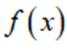
(2)对于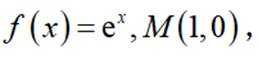
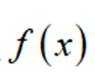
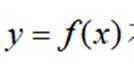
(3)已知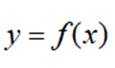
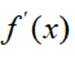

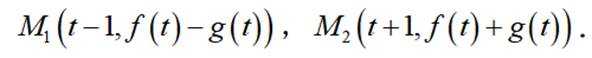
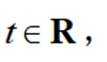
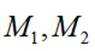
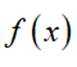
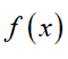
正确答案
(1)证明见解析
(2)存在,
(3)严格单调递减
解析
本题主要考察了函数的最值、导数的应用、新定义问题等知识点。
(1)证明
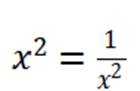
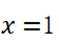
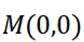
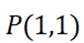
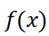
(2)
所以当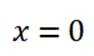
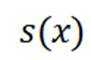
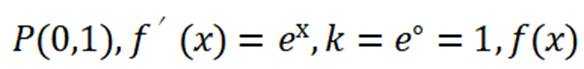
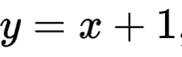

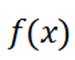
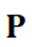
(3)对于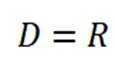
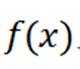
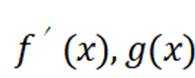
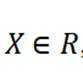
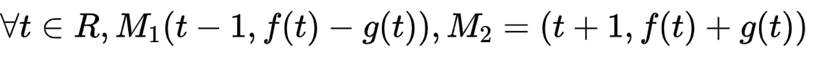
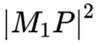
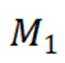
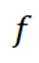
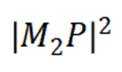
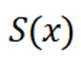
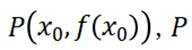

引理证明: