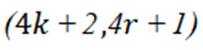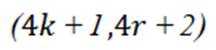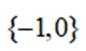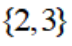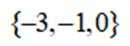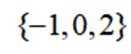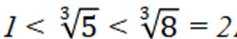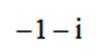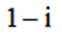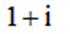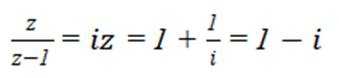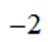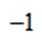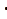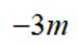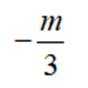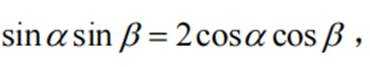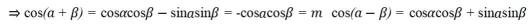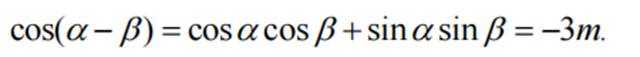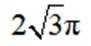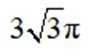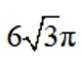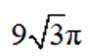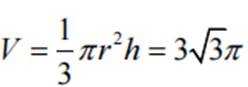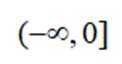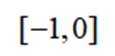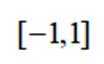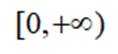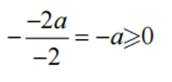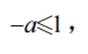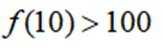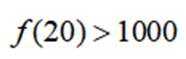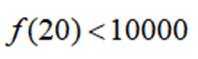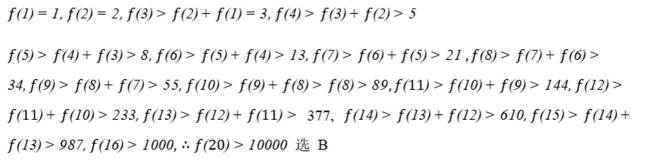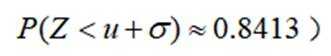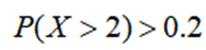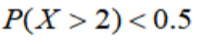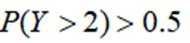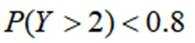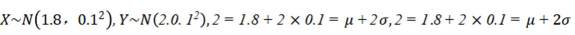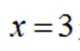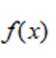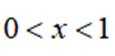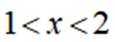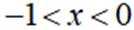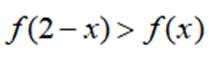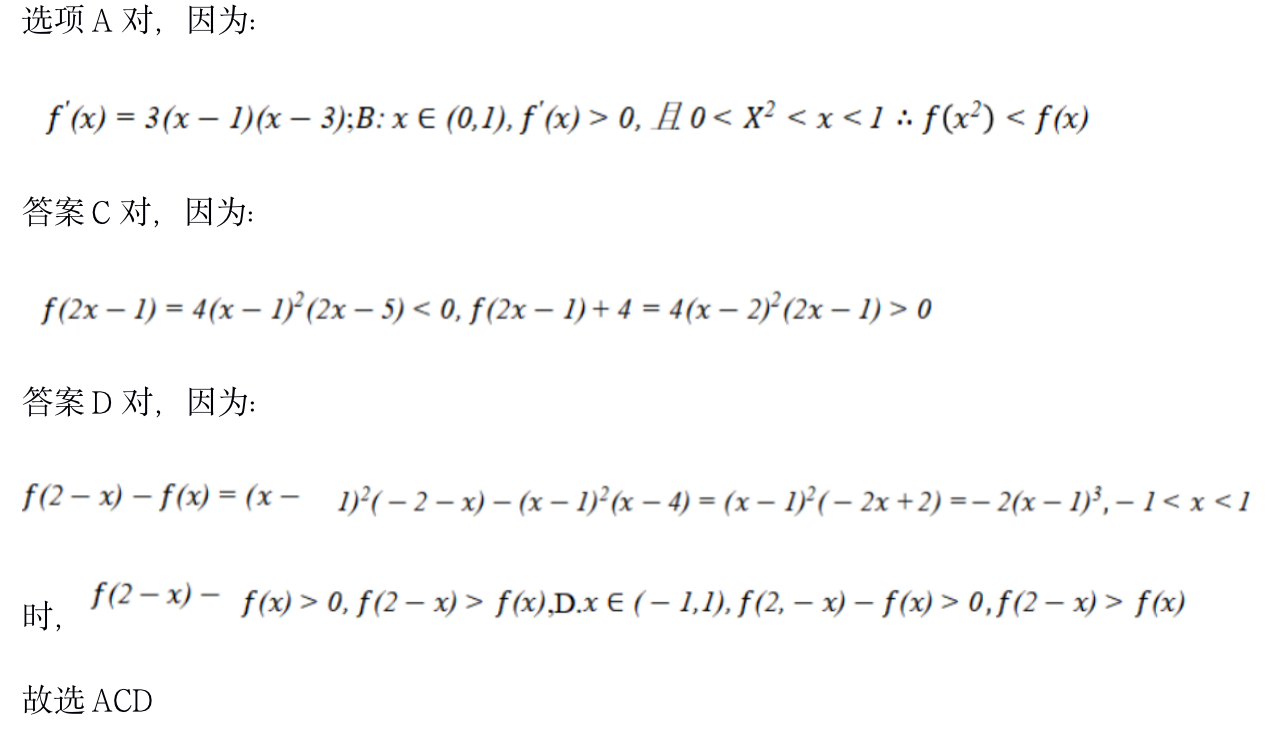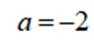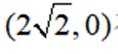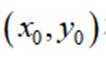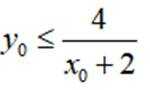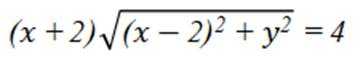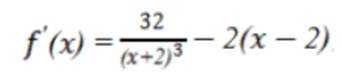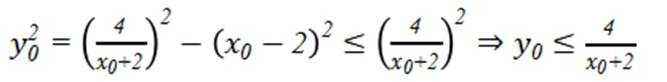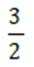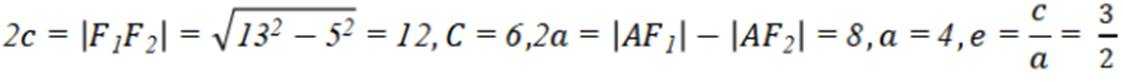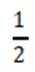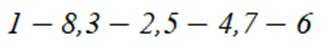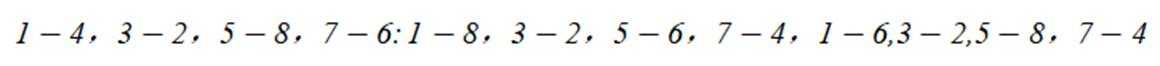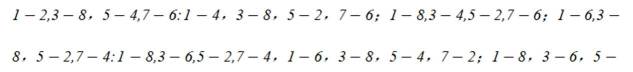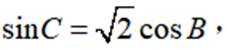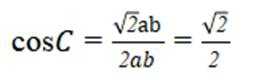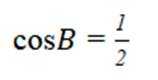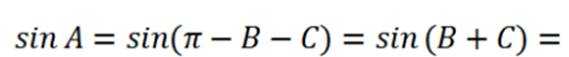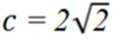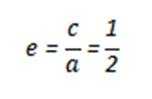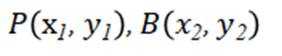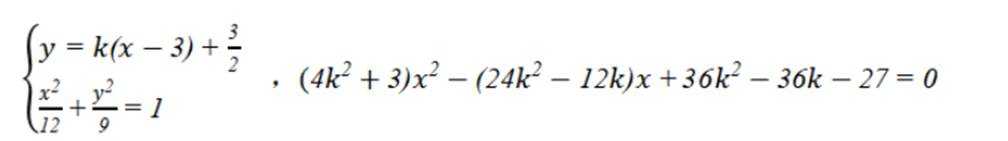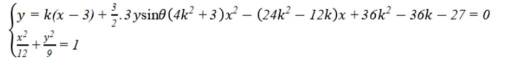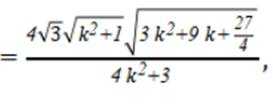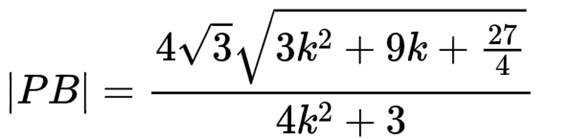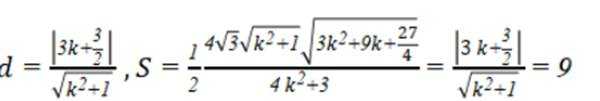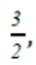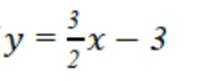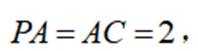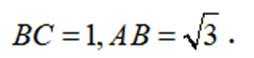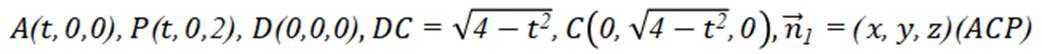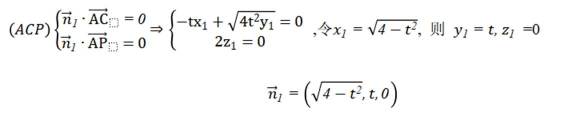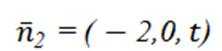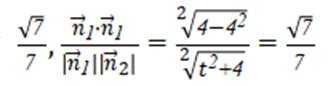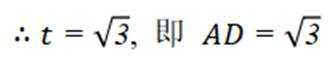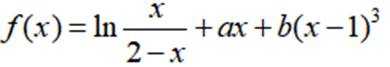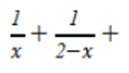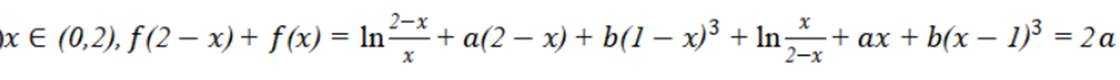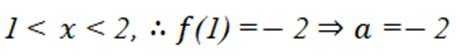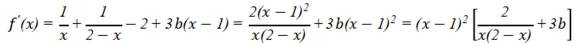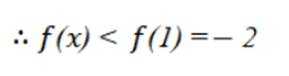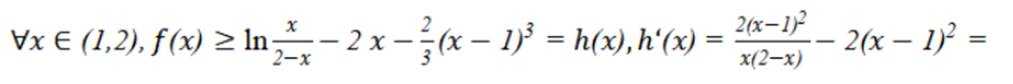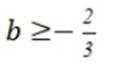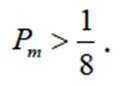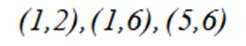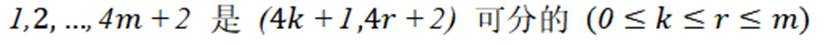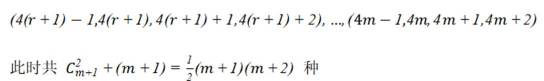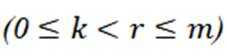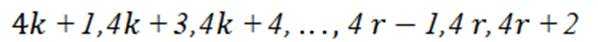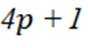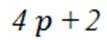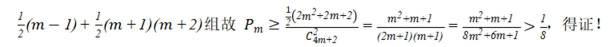已知集合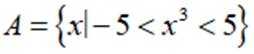
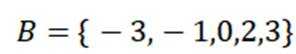
A
B
C
D
正确答案
解析
本题主要考查了集合的概念以及集合的交集运算，同时还涉及到对不等式条件的分析和判断。
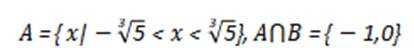
若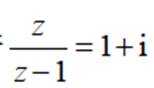
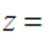
A
B
C
D
正确答案
解析
本题主要考查了复数的运算以及方程的求解。
已知向量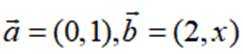
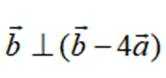
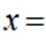
A
B
C1
D2
正确答案
解析
本题主要考查了向量垂直的性质以及向量的坐标运算等知识点。
由题可知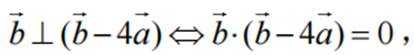
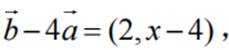
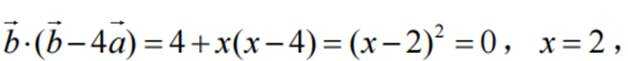
已知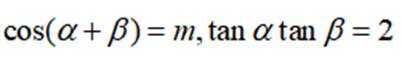
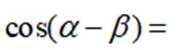
A
B
C
D
正确答案
解析
本题主要考查了三角函数的和差公式以及同角三角函数关系的知识点。
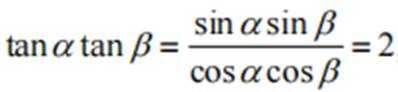
解得
已知圆柱和圆锥的底面半径相等，侧面积相等，且它们的高均为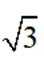
A
B
C
D
正确答案
解析
本题主要考查了圆柱和圆锥的侧面积公式、体积公式，以及方程的求解。还涉及到一些简单的几何关系和运算。
设圆锥与圆柱的地面半径为r，圆柱母线为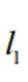
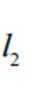
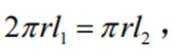
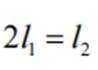
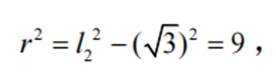
已知函数为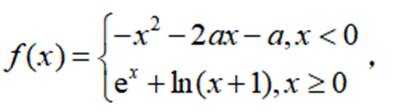
A
B
C
D
正确答案
解析
本题主要考查了分段函数的单调性、二次函数的单调性、指数函数与对数函数的单调性等知识点。
由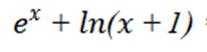
①
②
解得：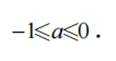
当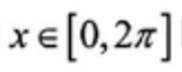
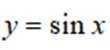
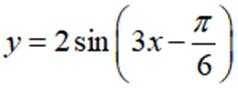
正确答案
解析
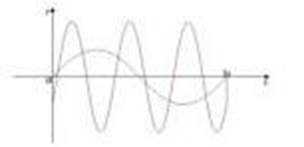
本题主要考查了三角函数的图像以及两个三角函数的图像交点问题。
作出两者图象，6个交点，选 C，
已知函数为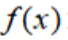
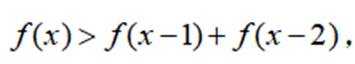
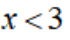
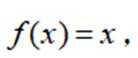
A
B
C
D
正确答案
解析
本题主要考查了函数的性质、不等式的运用以及对条件的分析推理能力。
为了解推动出口后的亩收入（单位：万元）情况，从该种植区抽取样本，得到推动出口后亩收入的样本均值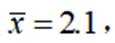
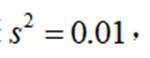
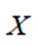
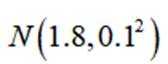
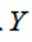
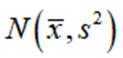
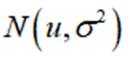
A
B
C
D
正确答案
解析
本题主要考查了正态分布的相关知识点。
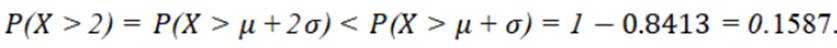
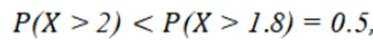
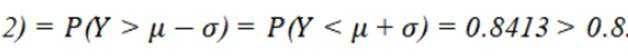
设函数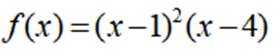
A
B当
C当
D当
正确答案
解析
本题主要考查了函数的极值、单调性，以及通过函数值的比较来分析问题等知识点。
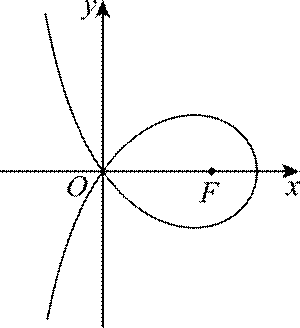
造型
A
B点
CC在第一象限的点的纵坐标的最大值为1
D当点
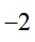
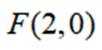
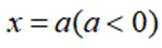
正确答案
解析
本题主要考查了曲线方程的建立、方程的变形与分析、点与方程的关系等知识点。
选项A对，因为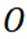
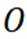
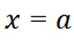
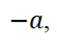
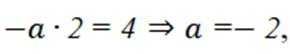
选项B对，因为代入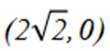
选项C错，因为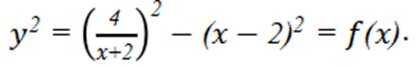
那么有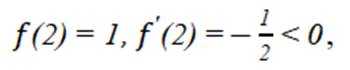
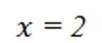
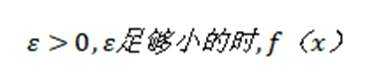
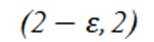
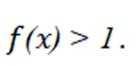
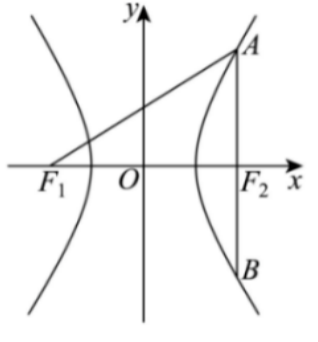
设双曲线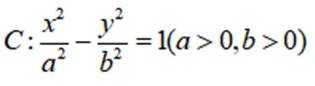
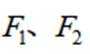
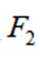
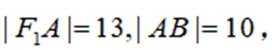
正确答案
解析
本题主要考查了双曲线的定义、双曲线的通径以及离心率的计算等知识点。
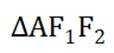
若曲线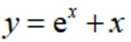
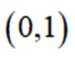
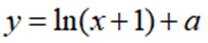
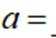
正确答案
解析
本题主要考查了导数的几何意义，利用导数求曲线的切线方程，以及两曲线切线的关系等知识点。
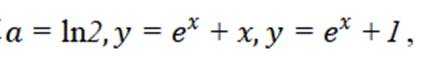
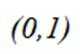
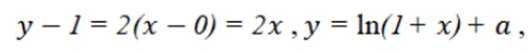
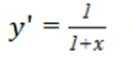
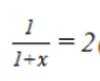
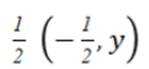
即：
甲、乙两人各有四张卡片，每张卡片上标有一个数字，甲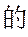
正确答案
解析
本题主要考查了概率的计算，以及通过列举等方法来分析各种情况。
甲出1一定输，所以最多3分，要得3分，就只有一种组合
得2分有三类，分别列举如下：
（1）出3和出5的赢，其余输：
（2）出3和出7的赢，其余输
（3）出5和出7的赢，其余输：
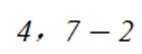
【分值】5
记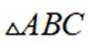
（1）求B；
（2）若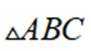
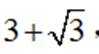
正确答案
（1）略；（2）略
解析
本题主要考查了余弦定理、正弦定理、三角形内角和定理以及三角形面积公式等知识点。
（1）已知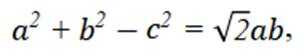
可得：
因为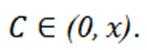
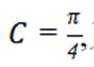
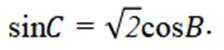
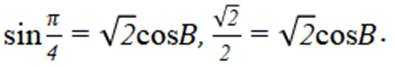
因为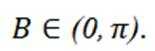
（2）
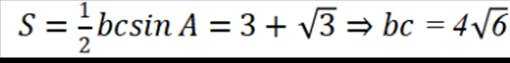
正弦定理：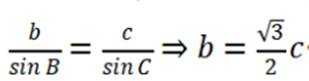
由①②得
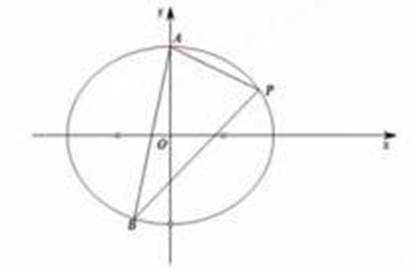
已知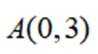
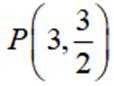
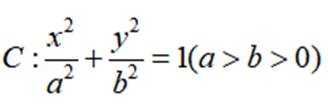
（1）求C的离心率；
（2）若过P的直线
正确答案
（1）略；（2）略
解析
本题主要考查了椭圆的标准方程、离心率的计算，以及直线方程、两点间的距离公式、平行线间的距离公式、三角形面积公式、柯西不等式等知识点。
（1）将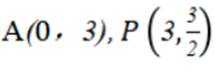
（2）当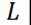 
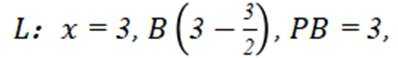
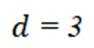
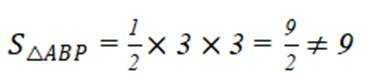
②当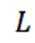
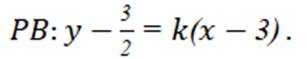
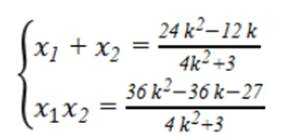
A到PE到的距离
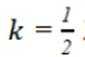
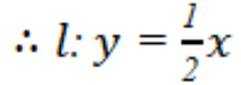
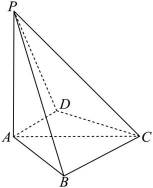
如图，四棱锥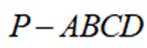
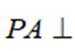
（1）若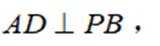
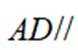
（2）若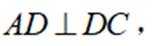
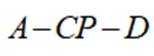
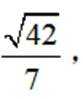
正确答案
（1）略；（2）略
解析
本题主要考查了线面平行的判定、勾股定理及其逆定理、线线垂直、二面角的相关知识，同时还涉及到空间向量在立体几何中的应用等知识点。
（1）
（2）以DA，DC为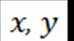
垂直的线为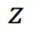 
令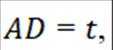
同理：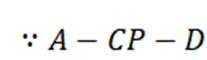
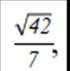
已知函数
（1）若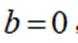
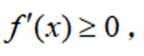
（2）证明：曲线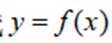
（3）若
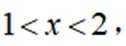
正确答案
（1）略；（2）略；（3）略
解析
本题主要考查了函数的导数、最值、对称性以及单调性等知识点。在解决问题中，还涉及到不等式的运用、函数的转化等知识。
(1) 
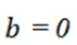
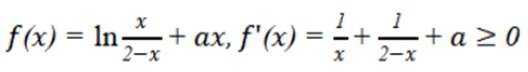
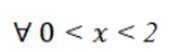
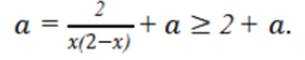
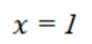
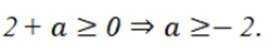
（2）
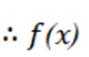
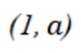
方法二：
将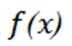
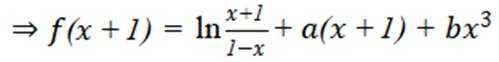
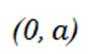
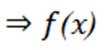
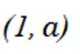
（3）
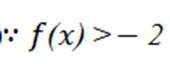
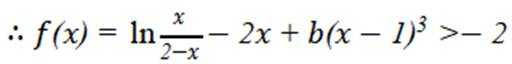
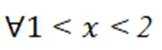
令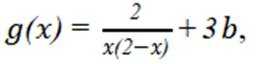
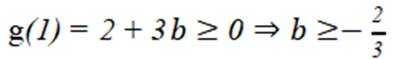
否则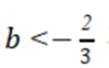
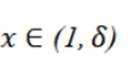
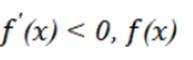
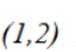
当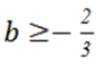
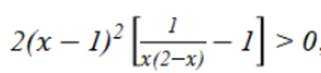
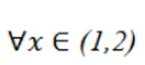
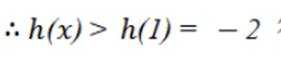
综上：
设m为正整数，数列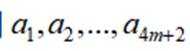
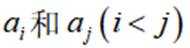
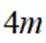
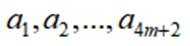
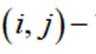
（1）写出所有的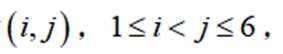
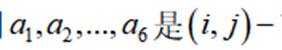
（2）当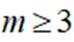
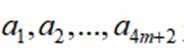
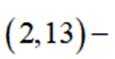
（3）从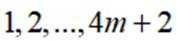
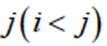
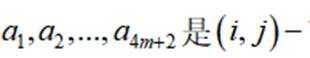
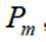
正确答案
（1）略；（2）略；（3）略
解析
本题主要考查了等差数列的概念、性质以及对新定义问题的理解和分析能力。
（1）以下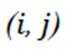
（2）易知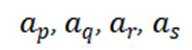
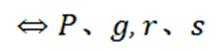
分组为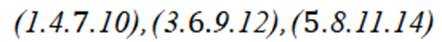
其余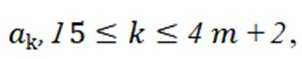 
（3）由第（2）问易发现：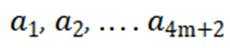
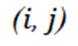
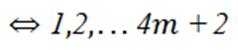
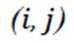
因为可分为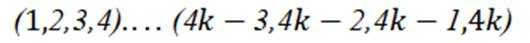
再证：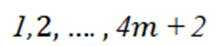 
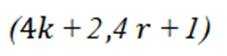
易知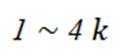
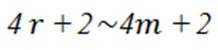
只需考虑
记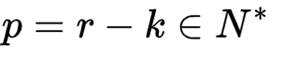
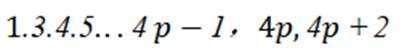
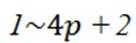
观察：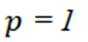 
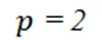
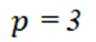
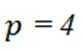
（1，5，9，13），（3，7，11，15），（4，8，12，16），（6，10，14，18）满足
故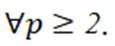
（1，p+1，2p+1，3p+1），（3，p+3，2p+3，3p+3），（4，p+4，2p+4，3p+4），（5，p+5，2p+5，3p+5），（p，2p，3p，4p），（p+2，2p+2，3p+2，4p+2）共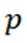
事实上，就是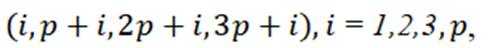
此时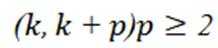
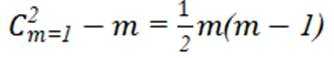
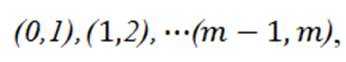
综上，可行的
