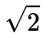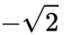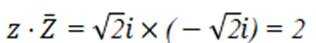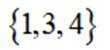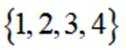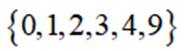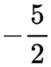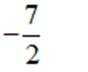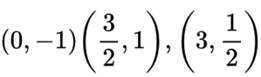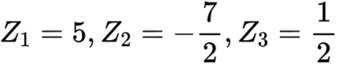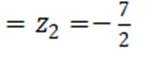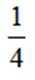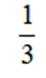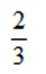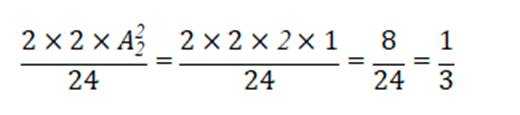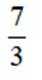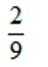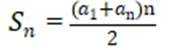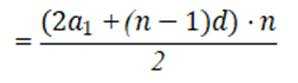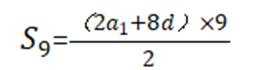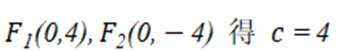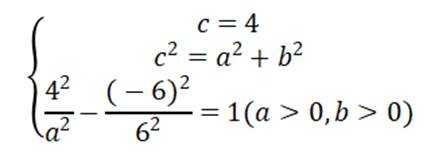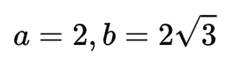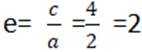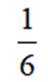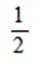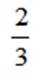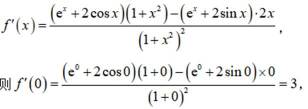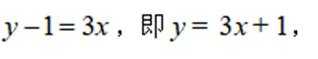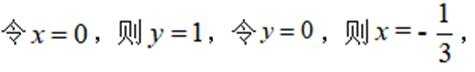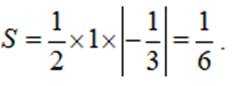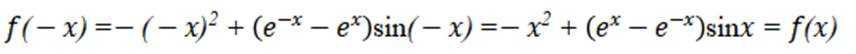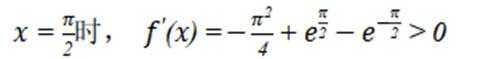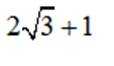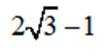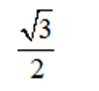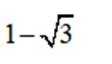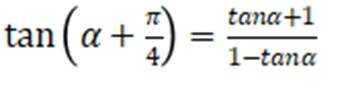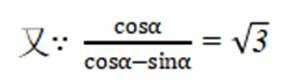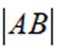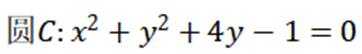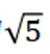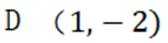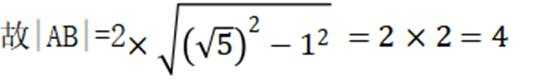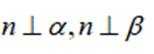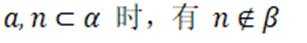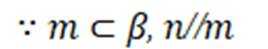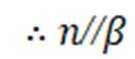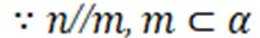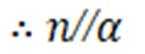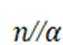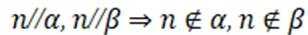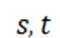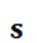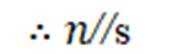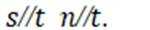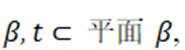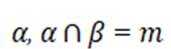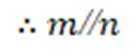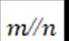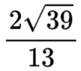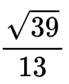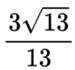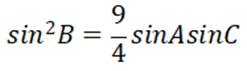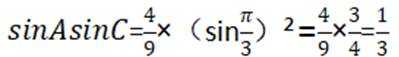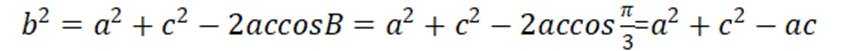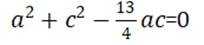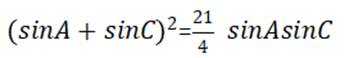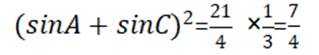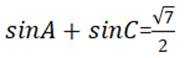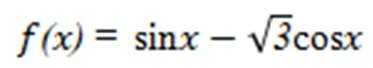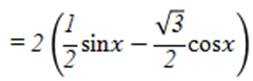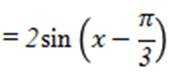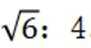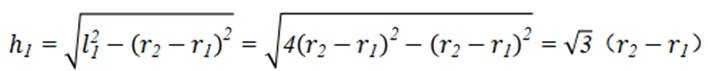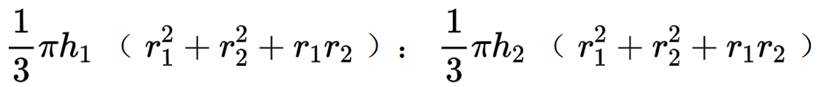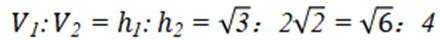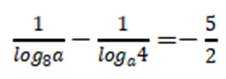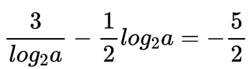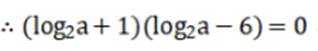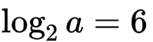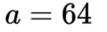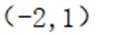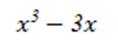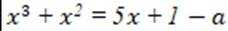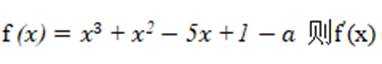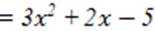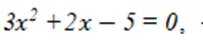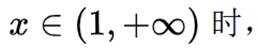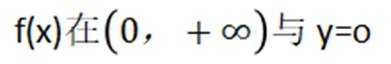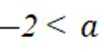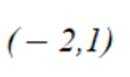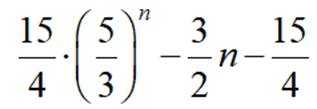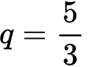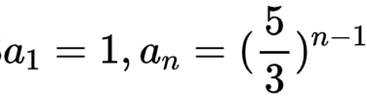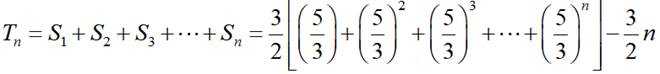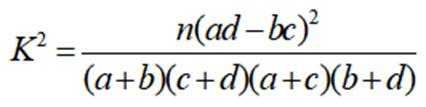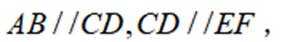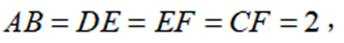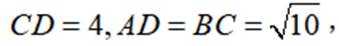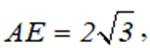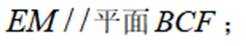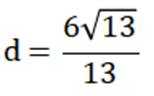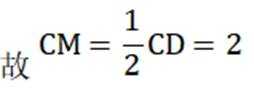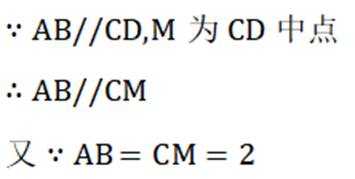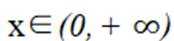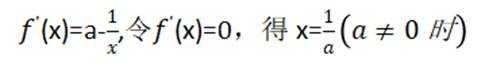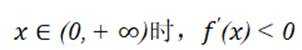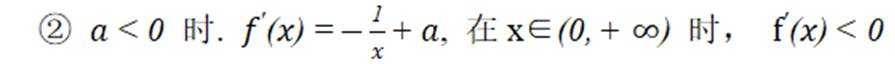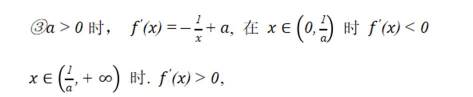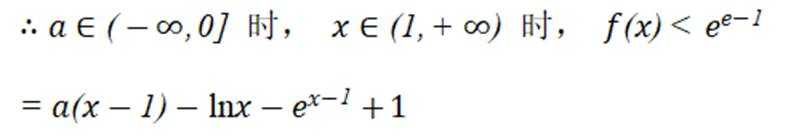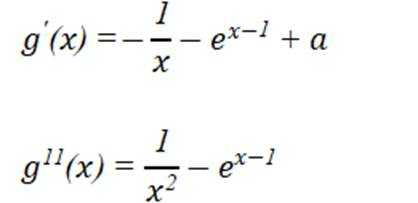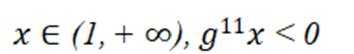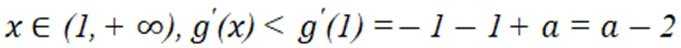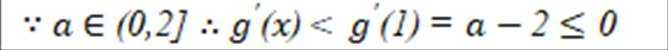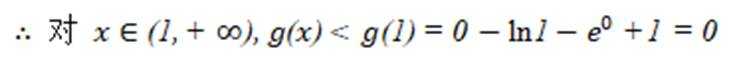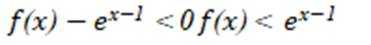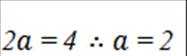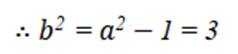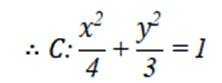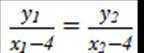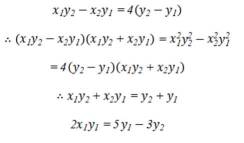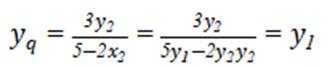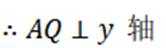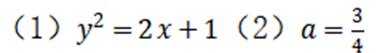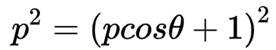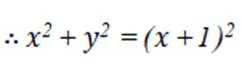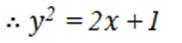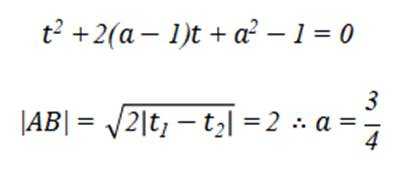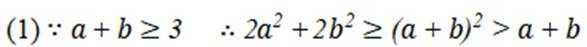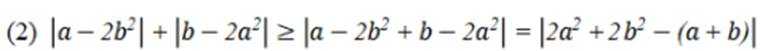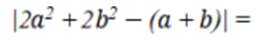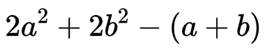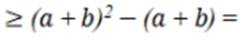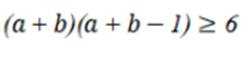- 真题试卷
- 模拟试卷
- 预测试卷
设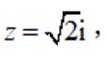
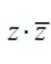
正确答案
解析
这道题主要考查了复数的运算。
在复数的运算中,我们需要掌握复数的基本形式:a+bi,其中a为实部,b为虚部。
则
集合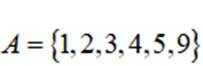
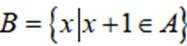
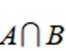
正确答案
解析
这道题主要考查了集合的运算和集合之间的关系。
集合的运算包括交集、并集、补集等。
交集是指两个集合中共同拥有的元素所组成的集合。
并集是指将两个集合中的所有元素合并在一起组成的集合。
补集则是在一个给定的全集范围内,某个集合在全集中的剩余部分。
依题意得,对于集合B中的元素x,满足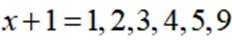
则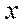
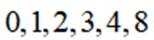
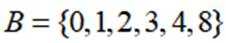
于是
故选:C
若实数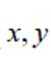
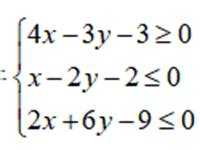

正确答案
解析
本题主要考查了线性规划的知识点。线性规划是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。
联立约束条件,得
代入函数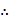
故选D.
甲、乙、丙、丁四人排成一列,丙不在排头,且甲或乙在排尾的概率是( )
正确答案
解析
这道题主要考查了排列组合以及古典概型的知识点。
在排列组合中,需要考虑不同元素的排列方式和数量。
古典概型则是通过计算事件发生的可能性总数以及所求事件发生的可能性数量,来得出概率。
由题意得,丙不在排头排尾,有2种位置选样
甲、乙、内、丁四人排成一列,共有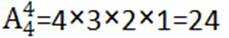
等差数列
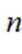
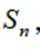
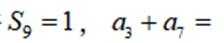
正确答案
解析
这道题主要考查了等差数列的通项公式和前 n 项和公式。
等差数列
则
已知双曲线
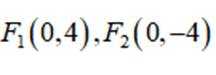
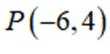
正确答案
解析
这道题主要考查了双曲线的定义和性质,重点是双曲线的离心率的计算
由
且双曲线C 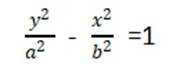
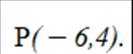
解得
得离心率
设函数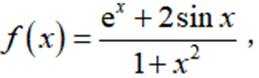
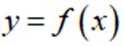
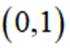
正确答案
解析
本题主要考查了导数的几何意义,通过求函数的导数来得到曲线在某一点的切线斜率,同时还涉及到三角形面积的计算。
即该切线方程为
故该切线与两坐标轴所围成的三角形面积
故选A
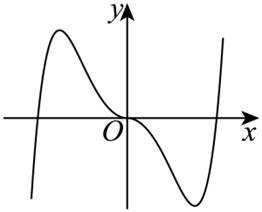
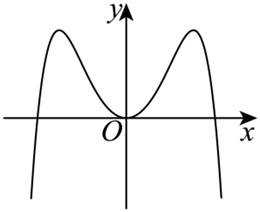
函数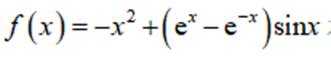
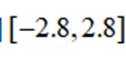
正确答案
解析
本题主要考查了函数的性质,包括奇偶性、单调性等,还涉及到一些基本函数的图像特征。
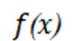
故排除 D项,选择B
已知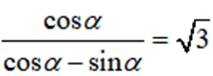
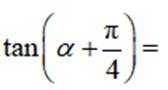
正确答案
解析
本题主要考查了三角函数的弦化切以及两角和的正切公式这两个知识点。
所以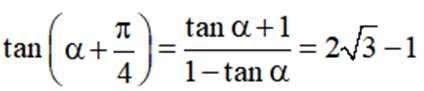
故选B
已知直线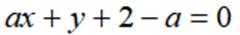
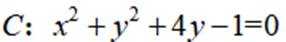
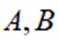
正确答案
解析
这道题主要考查了直线与圆的位置关系,以及弦长的计算。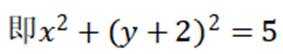
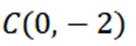
对直线
令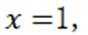
当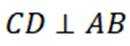
故选 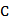
设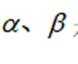
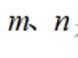
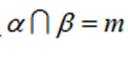
①若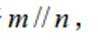
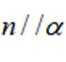
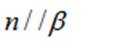
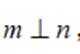
③若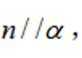
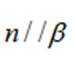
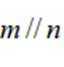
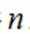

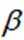
其中所有真命题
正确答案
解析
这道题主要考查了空间直线与平面的位置关系的相关知识点。
对①
又
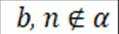
又
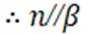
对②
如上图.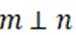

对③
即: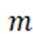
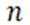
过 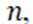
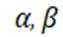
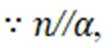
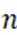
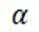
同理:
又 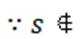
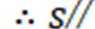
又 
则 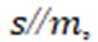
对④
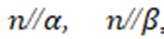
在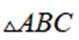
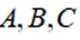
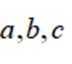
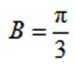
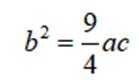
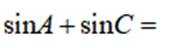
正确答案
解析
本题考查正弦定理,余弦定理的使用
结合正弦定理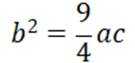
即
根据余弦定理得
结合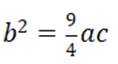
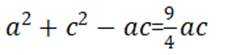
结合正弦定理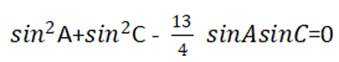
代入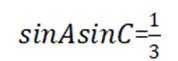
故
函数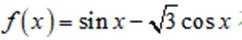
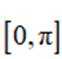
正确答案
2
解析
这道题主要考查了函数的单调性和最值的知识点。
因为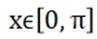
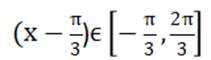
故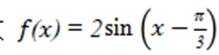
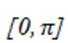
已知圆台甲、乙的上底面半径均为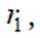
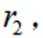
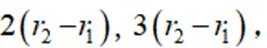
正确答案
解析
本题考查了圆台的体积公式以及相似图形的性质。
甲圆台高为
乙圆台的高为
所以圆台甲乙比为
即
已知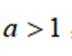
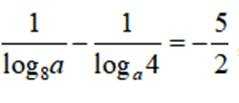
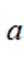
正确答案
64
解析
这道题主要考查了对数的运算性质
又因为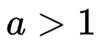
所以
曲线
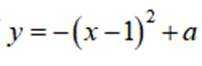
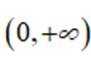
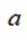
正确答案
解析
这道题主要考查了对数的运算性质等知识点
由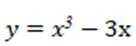
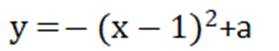
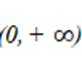
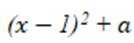
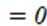
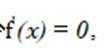
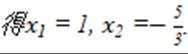
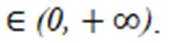
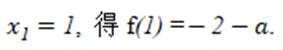

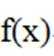
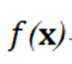
有两个不同交点。则
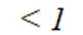

已知等比数列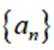
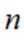
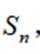
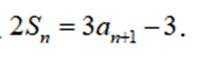
(1)求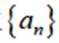
(2)求数列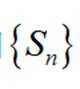
正确答案
(1)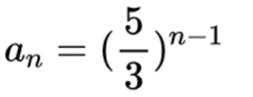
解析
这道题主要考查了函数与方程的转化,导数与函数单调性的关系,以及通过数形结合来解决问题
(1)因为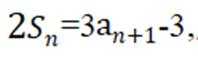
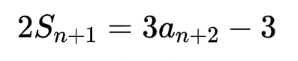
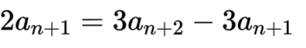
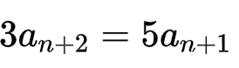
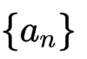
因为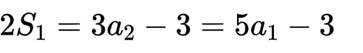
(2)由等比数列求和公式得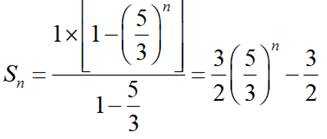
所以数列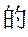
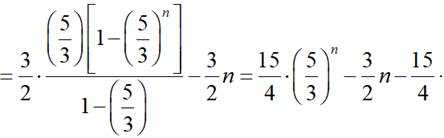
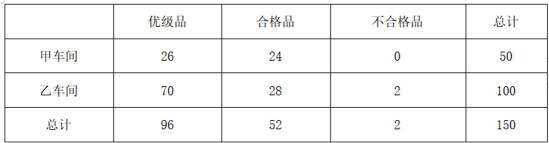
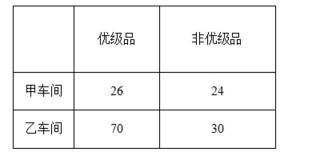
某工厂进行生产线智能化升级改造,升级改造后,从该工厂甲、乙两个车间的产品中随机抽取150件进行检验,数据如下:
(1)填写如下列联表:
能否有95%
(2)已知升级改造前该工厂产品的优级品率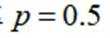
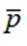
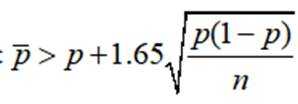
附:
正确答案
(1)没有99%的把握;(2)能
解析
这道题主要考查了统计与概率的知识点。包括对数据的整理分析,列联表的填写,以及利用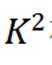
根据题意可得列联表:
可得
因为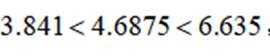
所以有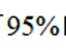

(2)由题意可知:生产线智能化升级改造后,该工厂产品的优级品的频率为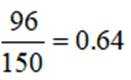
用频率估计概率可得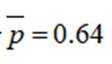
又因为升级改造前该工厂产品的优级品率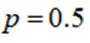
则
可知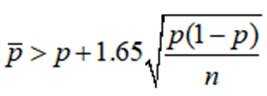
所以可以认为生产线智能化升级改造后,该工厂产品的优级品率提高了.
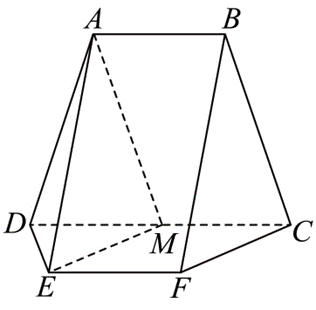
如图,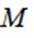
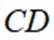
(1)证明:
(2)求点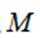
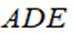
正确答案
(1)略(2)
解析
这道题主要考查了平行线的性质、三角形的相关知识以及勾股定理等知识点
(1)证:根据题意,M为CD中点
已知函数
(1)求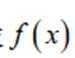
(2)若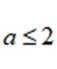
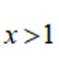
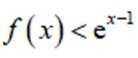
正确答案
(1)故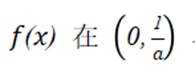
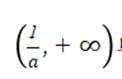
(2)略
解析
这道题主要考查了函数的单调性、导数的应用以及不等式的证明等知识点。
根据 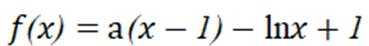
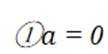
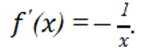
故此时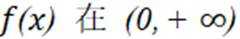
故此时 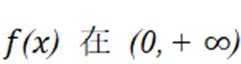
故此时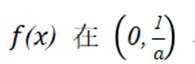
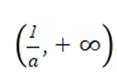
(2)①根据题(1). 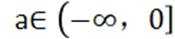
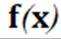
又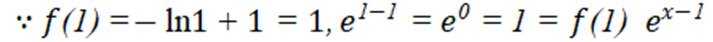
令 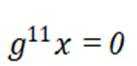
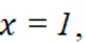
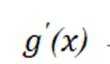
又
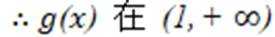
即
故若 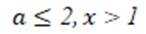
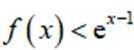
设椭圆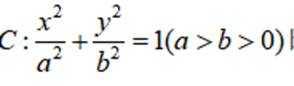

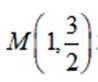
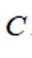
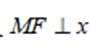
(1)求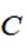
(2)过点
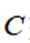
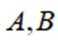
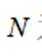
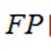

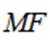
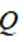
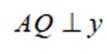
正确答案
(1)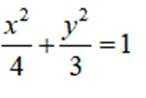
解析
本题主要考查了椭圆的标准方程、椭圆上的点的坐标特征、直线与椭圆的位置关系、中点坐标公式等知识点。
(1)
(2) 设 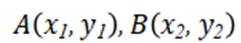
即
则
选考题:在平面直角坐标系
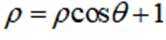
(1)写出
(2)设直线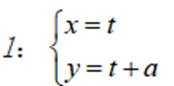
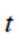
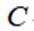
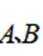
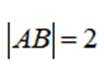
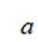
正确答案
解析
本题主要考查了极坐标方程与直角坐标方程的转化,以及直线参数方程的应用。
(1)
(2)将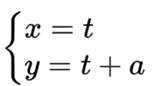
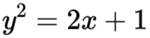
选考题:实数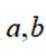
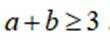
(1)证明: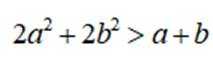
(2)证明: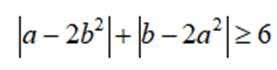
正确答案
(1)略(2)略