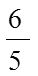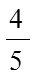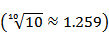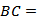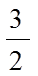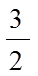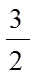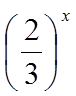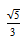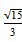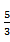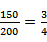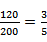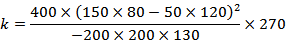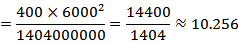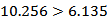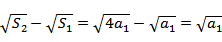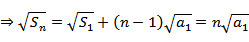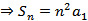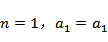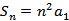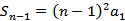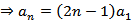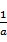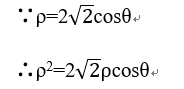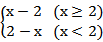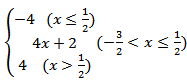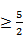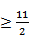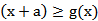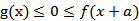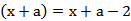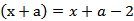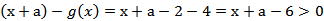- 真题试卷
- 模拟试卷
- 预测试卷
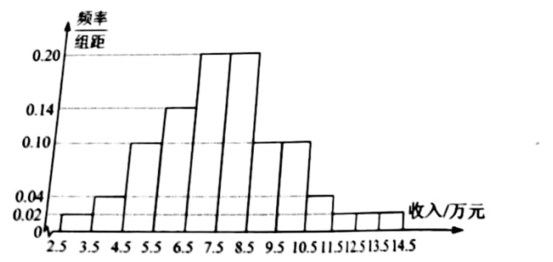
2.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是
正确答案
1.设集合M={1,3,5,7,9}. N={x|2x >7},则M∩N=
正确答案
5.点(3,0)到双曲线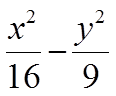
正确答案
6.青少年视力是社会普遍关注的问题,视力情况可借助视力表测量。通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录法的数据V满足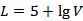
正确答案
8.在∆ABC中,已知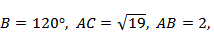
正确答案
9.记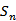
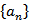
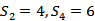
正确答案
10.将3个1和2个0随机排成一行,则2个0不相邻的概率为
正确答案
3.已知(1-i)2z =3+2i,则z =
正确答案
4.下列函数中是增函数的为
正确答案
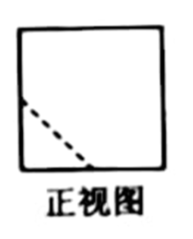
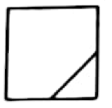
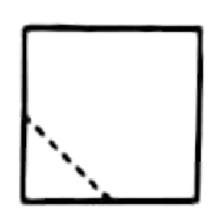
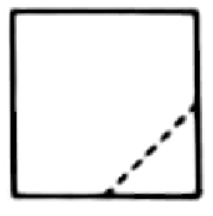
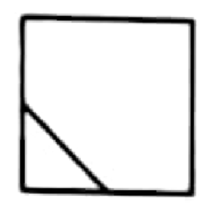
7.在一个正方体中,过顶点A的三条棱的中点分别为E, F, G,该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如右图所示,则相应的侧视图是
正确答案
11、若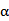
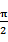
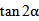
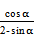
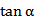
正确答案
12.设f(x)是定义域为R的奇函数,且f(1+x)=f(-x).若f(-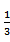
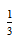
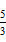
正确答案
15.已知函数f(x)=2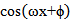

正确答案
-
13.若向量a,b满足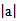
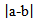
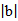
正确答案
3
14.已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为________.
正确答案
39π
16.已知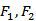
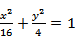
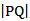
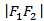
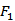
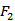
正确答案
8
17.(12 分)
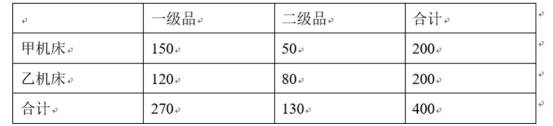
甲、乙两台机床生产同种产品产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品产品的质量情况统计如下表:
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)能否有99%的把握为机品质量与乙机床的产品质量有差异?
附: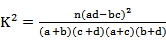
正确答案
(1)甲机床生产一级品150件,合计200件,故甲机床生产一级品的概率为
乙机床生产一级品120件,合计200件,故乙机床生产一级品的概率为
(2)由题意,
∵
∴有99%的把握认为军机床的产品质量与乙机床的产品质量有差异。
19.(12分)
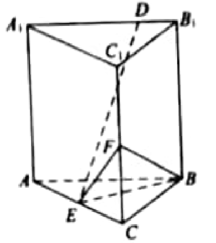
已知直三棱柱ABC-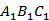

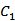
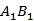
(1)求三棱锥F-EBC的体积:
(2)已知D为棱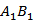
正确答案
(1) ∵直三棱柱ABC-A1B1C1,∴A1B1//AB,CC1⊥面ABC.
∵BF⊥A1B1,∴BF⊥AB.
∵正方形AA1B1B,∴AB⊥BB1,AB=BB1=2.
∵BF∩BB1=B,∴AB⊥面BB1C1C,∴AB⊥BC.
在Rt△ABC中,∵E为AC中点,AB=BC=2,
∴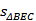
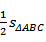
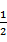
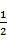
∵F是CC1中点,∴CF=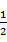
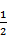
∴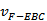
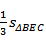
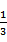
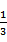
(2)连A1E,B1E,A1F,则A1E=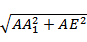
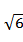
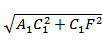
EF=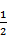
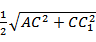
∴A1E2+EF2=A1F2,∴A1E⊥EF.
由(1)在Rt△ABC中,E是AC中点,∴BE⊥AC.
∵面AA1C1C⊥面ABC,面AA1C1C∩面ABC=AC,∴BE⊥面AA1C1C
∴BE⊥A1E
∵EF∩BE=E,∴A1E⊥面BEF,∴A1E⊥BF
∵BF⊥A1B1,A1B1∩A1E=A1,∴BF⊥面A1EB1
∵DE⊂面A1EB1,∴BF⊥DE.
18.(12 分)
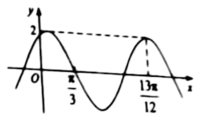
记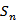
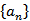
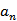
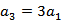
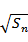
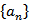
正确答案
由
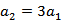
得
即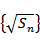
当
当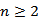
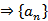
20.(12分)
设函数f(x)=
(1)讨论f(x)的单调性;
(2)若y=f(x)的图像与x轴没有公共点,求a的取值范围。
正确答案
f(x)=a2x2+ax-3lnx+1
(1)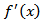

令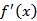
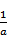
令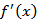
∴f(x)的增区间为(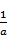
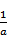
(2)由(1)知f(x)在(0,+∞)上的极小值为f(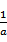
f(x)与x轴没有公共点,当且仅当f(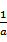
∴a2·(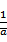
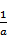
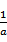
∴a>
21.(12分)
抛物线C的顶点为坐标原点O,焦点在x轴上,直线l:x=1交C于P,Q两点,且OP⊥OQ,已知点M(2,0),且⊙M与l相切。
(1)求C,⊙M的方程;
(2)设A1,A2,A3是C上的三个点,直线A1A2,A2A3均与⊙M相切,判断直线A2A3与⊙M的位置关系,并说明理由。
正确答案
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=
(1)将C的极坐标方程化为直角坐标方程;
(2)设点A的直角坐标为(1,0),M为C上的动点,点P满足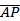

正确答案
(1)
∴x2+y2=2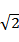
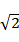
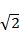
23. [选修4-5:不等式选讲](10分)
已知函数f(x)=|x-2|,g(x)=|2x+3|-|2x-1|。
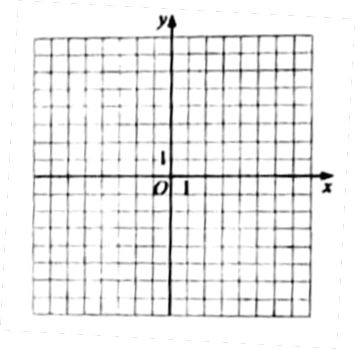
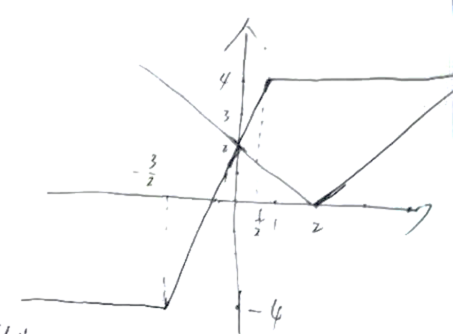
(1)画出y=f(x)和y=g(x)的图像;
(2)若f(x+a)≥g(x),求a的取值范围。
正确答案
(1)
f(x)=|x-2|=
g(x)=
如下图:
(2)
法1:当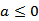
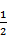
则f(x+a)<g(x)不成立
∴a>0
a>0时,由(1)知在(2-a,+∞)上f(x)↑
∴只需f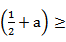
∴a的取值范围为[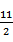
法二:
由(1)得
2-a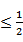
∵f(x)在[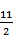
∴f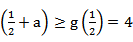
证明:当a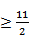
当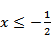
当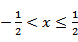
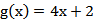
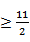
f
当x>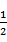
f
综上a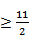
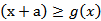
a的取值范围为[