- 真题试卷
- 模拟试卷
- 预测试卷
2.设
正确答案
解析



考查方向
解题思路
熟练掌握并运用复数的运算法则
易错点
复数的运算法则
知识点
5.直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的
正确答案
解析
如图,由题意得在椭圆中,
在



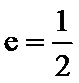
考查方向
解题思路
求解此类问题的一般步骤是先列出等式,再转化为关于a,c的齐次方程,方程两边同时除以a的最高次幂,转化为关于e的方程,解方程求e .
易错点
如何由a、c的方程转化成有关e的方程
知识点
6.若将函数y=2sin (2x+

正确答案
解析
考查方向
解题思路
平移规律:左加右减
易错点
一是平移方向,注意“左加右减“,二是平移多少个单位是对x而言的,不用忘记乘以系数.
知识点
7.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是
正确答案
解析
该几何体直观图如图所示:
考查方向
解题思路
由于三视图能有效的考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般常与几何体的表面积与体积交汇.由三视图还原出原几何体,是解决此类问题的关键.
易错点
由三视图正确还原出原几何体
知识点
9.函数

正确答案
解析
考查方向
解题思路
利用间接法,即由函数性质排除不符合条件的选项.
易错点
利用排除法合理的选择
知识点
1.设集合

正确答案
解析
考查方向
解题思路
集合是每年高考中的必考题,一般以基础题形式出现,属得分题.解决此类问题一般要把参与运算的集合化为最简形式再进行运算,如果是不等式解集、函数定义域及值域有关数集之间的运算,常借助数轴进行运算.
易错点
集合化简
知识点
3.为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率
正确答案
解析
将4种颜色的花种人选两种种在一个花坛中,余下2种种在另一个花坛,有6种种法,其中红色和紫色不在一个花坛的种数有4种,故概率为
考查方向
解题思路
按照一定的标准用列举法进行计数
易错点
用列举法计数时出现重复或遗漏
知识点
4.△ABC的内角A、B、C的对边分别为a、b、c.已知


正确答案
解析
由余弦定理得


考查方向
解题思路
本题属于基础题,考查内容单一,根据余弦定理整理出关于b的一元二次方程,再通过解方程求b.运算失误是基础题失分的主要原因,请考生切记!
易错点
余弦定理公式记忆
知识点
8.若

正确答案
解析
由



考查方向
解题思路
比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数单调性进行比较,若底数不同,可考虑利用中间量进行比较.
易错点
指数函数和对数函数的单调性
知识点
10.执行右面的程序框图,如果输入的

正确答案
解析
第一次循环:
第二次循环:
第三次循环:



考查方向
解题思路
求解此类问题一般是把人看作计算机,按照程序逐步列出运行结果.
易错点
认清循环结构的起始值、步长
知识点
11.平面




正确答案
解析
考查方向
解题思路
求解此类问题一般是把人看作计算机,按照程序逐步列出运行结果.
易错点
正确作出异面直线所成角
知识点
12.若函数

正确答案
解析
考查方向
解题思路
本题把导数与三角函数结合在一起进行考查,有所创新,求解关键是把函数单调性转化为不等式恒成立,再进一步转化为二次函数在闭区间上的最值问题,注意与三角函数值域或最值有关的问题.
易错点
与三角函数值域或最值有关的问题,要注意弦函数的有界性.
知识点
13.设向量a=(x,x+1),b=(1,2),且a 
正确答案
解析
由题意,
考查方向
解题思路
本题所用到的主要公式是:若

易错点
准确记忆公式,注意运算的准确性.
知识点
15.设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若
正确答案
解析
考查方向
解题思路
如圆的半径r、弦长l、圆心到弦的距离d之间的关系:
易错点
记忆求圆心坐标、半径、弦长时常用圆的几何性质
知识点
16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元.
正确答案
解析
设生产产品





目标函数
取得最大值.解方程组


所以当


故生产产品


考查方向
解题思路
设未知量,列约束条件和目标函数,画出约束条件表示的可行域,利用平移找出最优解并解出,最后作答.
易错点
运算失误
知识点
14.已知θ是第四象限角,且sin(θ+


正确答案
解析
由题意
因为

从而


考查方向
解题思路
利用整体法灵活变换角.
易错点
三角函数求值,若涉及到开方运算,要注意根式前正负号的取舍,同时要注意角的灵活变换.
知识点
已知


17.求
18.求
正确答案
解析
:
考查方向
解题思路
易错点
将等差、等比数列中的五个基本量转化成方程应用题,注意运算.
正确答案
解析
(II)由(I)和






考查方向
解题思路
易错点
将等差、等比数列中的五个基本量转化成方程应用题,注意运算.
某公司计
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),
21.若
22.若要求“需更换的易损零件数不大于

23.假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
正确答案
解析
考查方向
解题思路
易错点
读题、审题.
正确答案
19
解析
(2)由柱状图知,需更换的零件数不大于18的概率为0.46,不大于19的概率为0.7,故
考查方向
解题思路
易错点
读题、审题.
正确答案
19
解析
(Ⅲ)若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台

比较两个平均数可知,购买1台机器的同时应购买19个易损零件.
考查方向
解题思路
易错点
读题、审题.
在直角坐标系

24.求
25.除H以外,直线MH与C是否有其它公共点?说明理由.
正确答案
2
解析
考查方向
解题思路
先确定










易错点
合理巧设参变量、化归思想、运算能力.
正确答案
没有
解析
直线


直线










考查方向
解题思路
把直线









易错点
合理巧设参变量、化归思想、运算能力.
如图,在已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点E,连接PE并延长交AB于点G.
19.证明G是AB的中点;
20.在答题卡第(18)题图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
正确答案
见解析
解析
(I)因为


因为


所以

又由已知可得,


考查方向
解题思路
易错点
应用定理时一定要写全定理的条件.
正确答案
作图见解析,体积为
解析
(II)在平面







理由如下:由已知可得








连接





由(I)知,



由题设可得




由已知,正三棱锥的侧面是直角三角形且
在等腰直角三角形

所以四面体
考查方向
解题思路
易错点
应用定理时一定要写全定理的条件.
已知函数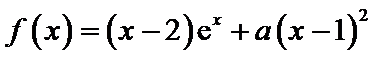
26.讨论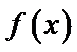
27.若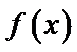
正确答案
见解析
解析
(I)
(i)设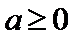
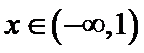
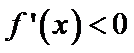
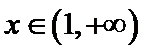
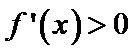
所
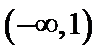
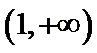
(ii)设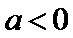
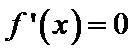
①若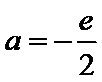
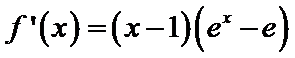
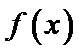
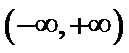
②若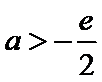
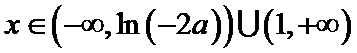
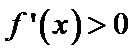
当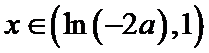
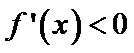
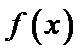
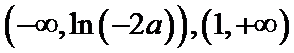
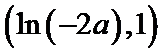
③若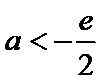
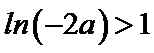


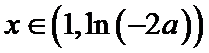
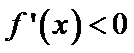
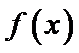
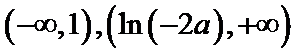
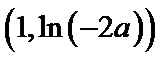
考查方向
解题思路
(I)先求得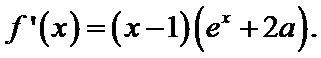
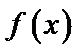
易错点
分类讨论思想及分类讨论原则、合理构造新函数.
正确答案
解析
考查方向
解题思路
(II)借助第一问的结论,通过分类讨论函数单调性,确定零点个数,从而可得a的取值范围为
易错点
分类讨论思想及分类讨论原则、合理构造新函数.
请考生在以下3题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号
【选修4-1:几何证明选讲】(请回答28、29题)
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,
【选修4—4:坐标系与参数方程】(请回答30、31题)
在直角坐标系x


在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=
【选修4—5:不等式选讲】(请回答32、33题)
已知函数
28.证明:直线AB与
29.点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
30.说明C1是哪一种曲线,并将C1的方程化为极坐标方程;
31.直线C3的极坐标方程为


32.在答题卡第(24)题图中画出
33.求不等式
正确答案
见解析
解析
在






考查方向
解题思路
易错点
熟悉相关定理及性质并灵活应用.
正确答案
见解析
解析
(Ⅱ)因为





由已知得




同理可证,

考查方向
解题思路
易错点
熟悉相关定理及性质并灵活应用.
正确答案
圆,
解析



∴


∵


考查方向
解题思路
易错点
熟记极坐标方程与参数方程的互化公式及应用.
正确答案
1
解析








①—②得:
∴
考查方向
解题思路
易错点
熟记极坐标方程与参数方程的互化公式及应用.
正确答案
见解析
解析
如图所示:
考查方向
解题思路
易错点
绝对值不等式的解法、分段函数的转化、不等式的解集一定要写成集合的形式.
正确答案
解析
考查方向
解题思路
易错点
绝对值不等式的解法、分段函数的转化、不等式的解集一定要写成集合的形式.