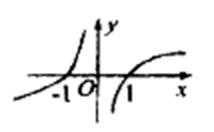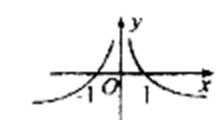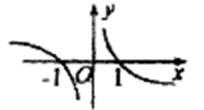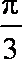- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集U={a,b,c,d},集合A={a,b},B={b,c,d},则(∁UA)∪(∁UB)=( )
正确答案
解析
∵U={a,b,c,d},集合A={a,b},B={b,c,d},
∴(∁UA)∪(∁UB)={c,d}∪{a}={a,c,d},
故选:D
知识点
2.复数
正确答案
解析
∵

∴复数

故选:C.
知识点
3.设x、y是两个实数,命题“x、y中至少有一个数大于1”成立的充分不必要条件是( )
正确答案
解析
若
所以
所以x+y>2是x、y中至少有一个数大于1成立的充分不必要条件.
故选B
知识点
5.函数y=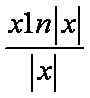
正确答案
解析
易得函数是奇函数,故排除A、C选项,又当x>0时函数为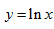
知识点
6.一个几何体的三视图如下图所示,且其左视图是一个等边三角形,则这个几何体的体积为
正确答案
解析
此几何体是底面半径为1的半圆锥,与底面是边长为2的正方形的四棱锥构成的组合体,它们的顶点相同,底面共面,高为边长为2的正三角形的高
知识点
7.已知x,y满足约束条件
正确答案
解析
由约束条件
联立
B(3,0),
化目标函数z=2x+y为y=﹣2x+z,
由图可知,当直线y=﹣2x+z过A时,直线在y轴上的截距最小,z最小等于2×1﹣1=1;
当直线y=﹣2x+z过B时,直线在y轴上的截距最大,z最大等于2×3﹣0=6.
∴a+b=1+6=7.
故选:A.
知识点
8.已知函数y=f(x)是R上的偶函数,当x1,x2∈(0,+∞)时,都有(x1﹣x2)•[f(x1)﹣f(x2)]<0.设
正确答案
解析
根据已知条件便知f(x)在(0,+∞)上是减函数;
且f(a)=f(|a|),f(b)=f(|b|),f(c)=f(|c|);
|a|=lnπ>1,b=(lnπ)2>|a|,c=
∴f(c)>f(a)>f(b).
故选:C.
知识点
9.若把函数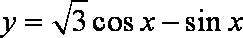
正确答案
解析
由题意知,
对称轴方程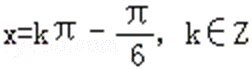

知识点
4.如图程序框图中,若输入m=4,n=10,则输出a,i的值分别是( )
正确答案
解析
模拟执行程序,可得
m=4,n=10,i=1
a=4,
不满足条件n整除a,i=2,a=8
不满足条件n整除a,i=3,a=12
不满足条件n整除a,i=4,a=16
不满足条件n整除a,i=5,a=20
满足条件n整除a,退出循环,输出a的值为20,i的值为5.
故选:C.
知识点
10.已知D是


正确答案
解析
由于D是△ABC中边BC上(不包括B、C点)的一动点,且满足


所以

知识点
12.定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=4,则不等式exf(x)>ex+3(其中e为自然对数的底数)的解集为( )
正确答案
解析
解:设g(x)=exf(x)﹣ex,(x∈R),
则g′(x)=exf(x)+exf′(x)﹣ex=ex[f(x)+f′(x)﹣1],
∵f(x)+f′(x)>1,
∴f(x)+f′(x)﹣1>0,
∴g′(x)>0,
∴y=g(x)在定义域上单调递增,
∵exf(x)>ex+3,
∴g(x)>3,
又∵g(0)═e0f(0)﹣e0=4﹣1=3,
∴g(x)>g(0),
∴x>0
故选:A.
知识点
11.已知椭圆







正确答案
解析
由已知得椭圆


∵|AF|=4,由抛物线的定义得,
∴A到准线的距离为4,即A点的纵坐标为2,又点A在抛物线上,
∴从而点A的坐标A(4,2);坐标原点关于准线的对称点的坐标为B(0,-4)
则|PA|+|PO|的最小值为:|AB|=
知识点
20.已知椭圆




(1)求椭圆
(2)是否存在与椭圆





正确答案
(1) 
解析
(1)设椭圆








所以椭圆

(2)解:存在直线

由



设


若






化简得,






从而


所以实数

知识点
17.设



(1)求角
(2)若


正确答案
见解析。
解析
(1)由已知及正弦定理可得
整理得
所以
又

(2)由正弦定理可知



所以
又


若


若


知识点
19.已知函数
(1)若
(2)若函数在
正确答案
(1)当

解析
(1)显然函数定义域为(0,+
令
当
当
(2)
令
当
当
故当

知识点
18.2015年春晚过后,为了研究演员上春晚次数与受关注度的关系,某站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
(1)若该演员的粉丝数量


(2)若用
(a)求这5次统计数据时粉丝的“即时均值”的方差;
(b)从“即时均值”中任选3组,求这三组数据之和不超过20的概率.
参考公式:
正确答案
(1)


解析
(1)由题意可知,
当
即该演员上春晚12次时的粉丝数约为122万人.
(2)经计算可知,这五组数据对应的“即时均值”分别为:5,5,7,10,10
(ⅰ)这五组“即时均值”的平均数为:7.4,则方差为
(ⅱ)这五组“即时均值”可以记为


知识点
21.如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE = EF.
正确答案
见解析。
解析
(1)

又



(2)




知识点
22.在直角坐标系







(1)若直线


(2)设


正确答案
(1)
解析
(1)将曲线


直线


将








(2)曲线









知识点
15.如图放置的正方形






正确答案
2
解析
解:如图令∠OAD=θ,由于AD=1故0A=cosθ,OD=sinθ,
如图∠BAX= 





同理可求得
∴
的最大值是2,故答案是 2
知识点
13.若双曲线E的标准方程是
正确答案
y=
解析
双曲线E的标准方程是
则a=2,b=1,
即有渐近线方程为y=
即为y=
故答案为:y=
知识点
14.已知{an}是等比数列,
正确答案
解析
由 

数列{anan+1}仍是等比数列:其首项是a1a2=8,公比为
所以,
故答案为
【点评】: 本题主要考查等比数列通项的性质和求和公式的应用.应善于从题设条件中发现规律,充分挖掘有效信息.
知识点
16.在等腰梯形












正确答案
解析
解:设DC的中点为F,PE的中点为H,连接FH由折叠的三棱人锥可知球心O在FH上,