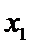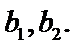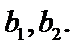- 真题试卷
- 模拟试卷
- 预测试卷
1. 已知全集


正确答案
解析
考查补集与交集的运算。因为

故选D.
考查方向
解题思路
先根据题意求

易错点
本题是基础题,解题时只要认真审题,不会出错,属于送分题。
知识点
2.已知

正确答案
解析
分母实数化,即分子与分母同乘以分母的其轭复数
故选 A.
考查方向
解题思路
化简
易错点
本题只要注意分母实数化就可以了,较易,属于送分题。
知识点
3.已知非零平面向量


正确答案
解析
因为

展开,合并同类项,得:

故选C。
考查方向
解题思路
等价转换“

易错点
本题易在“
知识点
4.执行如图所示的程序框图,输出的
正确答案
解析
依次执行结果如下:
S=2×1+1=3,i=1+1=2,i<4;
S=2×3+2=8,i=2+1=3,i<4;
S=2×8+1=19,i=3+1=42,i≥4;
所以,S=19,选B。
故选B
考查方向
解题思路
分条件不断赋值得到S
易错点
本题是框图运算类问题,考生只要会依次不断赋值,不会出错,属于送分题。
知识点
5.在



正确答案
解析
因为
所以,


故选:C
考查方向
解题思路
由条件利用正弦定理化简
易错点
本题在利用正弦定理化简
知识点
6.已知某四棱锥的三视图如图所示,则该四棱锥的侧面积是
正确答案
解析
由三视图得四棱锥如下图所示,
故选B。
考查方向
解题思路
由三视图得到几何体为一个四棱锥。根据直观图计算各个侧面面积,即可。
易错点
本题在把几何体的还原成平面直观图上易出错。
知识点
8. 若圆


正确答案
解析
只需求圆心(0,1)到曲线


距离
所以,若圆与曲线无公共点,则0< r<
故选C。
考查方向
解题思路
先根据题意取曲线上的点


易错点
本题易在理解题意上出现错误。本题易在用变量得到距离后求最值时极易出错。
知识点
7. 某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是
正确答案
解析
读图可知A、B、C均正确,对于D,前6 个月的平均收入
故选D。
考查方向
解题思路
读图可知A、B、C均正确。对于D,可通过计算再行确认。
易错点
本题易看错题目中“错误”二字导致选错。
9.已知函数

正确答案
2
解析
因为

故此题答案为2。
考查方向
解题思路
先算出

易错点
本题属于分段函数求值问题,只要计算不出错就不易出现问题。
知识点
10.已知双曲线

正确答案
解析
抛物线

所以,

故此题答案为
考查方向
解题思路
先根据题意抛物线的焦点坐标为(2,0)从而得出

易错点
本题较简单,只要抛物线的定义及双曲线渐近线方程等知识熟知就不会出错。
知识点
12.已知不等式组



正确答案
解析
出不等式表示的平面区域,如图所示,
即B(3,3),A(1,1),
故此题答案为
考查方向
解题思路
根据不等式组画平面区域,并找出(-1,0)点。过(-1,0)点转动直线与可行域有交点时找出最优解,从而得到
易错点
本题易在

知识点
1










正确答案


解析
由|PA|=|PB|
则|AC|=
xA=2,代入圆方程
即 A(2,3)或(2,7),故直线l 的方程为:
故此题答案为

考查方向
解题思路
由|PA|=|PB|则|AC|=

易错点
本题在“

知识点
11.已知递增的等差数列







正确答案


解析
故此题答案为

考查方向
解题思路
先根据



易错点
本题易在求和项数的判断上出现错误。
知识点
14.甲乙两人做游戏,游戏的规则是:两人轮流从1(1必须报)开始连续
正确答案
1,2,3,4
解析
甲先报1,2,3,4,然后不管乙报几个数,甲只需要每次报的数的个数与乙的个数
和为8(显然这可以做到),因为100-4=96=8×12 ,于是12轮过后,甲获胜.
故此题答案为1,2,3,4。
考查方向
解题思路
本题总数为8的倍数时,对方先报,自己就一定能报到最后一个数,100=6×16+4=12×8+4。如果甲先报数,就先报4个数,100-4=96。然后无论乙报几个数,甲所报个数与乙的个数之各为8,这样保证甲一定获胜。
易错点
本题不易读懂题意,特别是对“每人一次最少要报一个数,最多可以连续报7个数”的理解不到位。本题易出现逻辑上的混乱,从而导致判断出错。
知识点
已知数列



17.求数列
18.若



正确答案
an=22n-1;
解析
试题分析:本题属于等差数列通项求法与求和的应用问题,题目的难度适中。(1)求解时一定要灵活应用




(Ⅰ)由
当
当


所以数列


考查方向
解题思路
本题考查了等差数列的通项公式和求和公式的应用及性质,解题步骤如下:
由数列前



对于

易错点
由数列前


正确答案
证明略。
解析
试题分析:本题属于等差数列通项求法与求和的应用问题,题目的难度适中。(1)求解时一定要灵活应用




由(Ⅰ)可得
当
当

综上,
考查方向
解题思路
本题考查了等差数列的通项公式和求和公式的应用及性质,解题步骤如下:
由数列前



对于

易错点
由数列前


已知函数


15.求
16.求


正确答案
1;
解析
试题分析:本题属于三角公式与三角函数综合应用问题,题目的难度适中。(1)化简时一定要结合半倍角公式及辅助角公式灵活应用;(2)第二问属于给定区间求三角函数最值问题,只要注意此种问题的方法即可。
(Ⅰ)

因为


考查方向
解题思路
由已知利用半角公式与辅助角公式对
第二问按照“给定区间”求函数最值的方法结合正弦函数的性质得出f(x)的最值。
易错点
本题在第一问对


正确答案
(2)最大值为

解析
试题分析:本题属于三角公式与三角函数综合应用问题,题目的难度适中。(1)化简时一定要结合半倍角公式及辅助角公式灵活应用;(2)第二问属于给定区间求三角函数最值问题,只要注意此种问题的方法即可。
(Ⅱ)由(Ⅰ)可知
因为

则
当



当







考查方向
解题思路
由已知利用半角公式与辅助角公式对
第二问按照“给定区间”求函数最值的方法结合正弦函数的性质得出f(x)的最值。
易错点
本题在第一问对


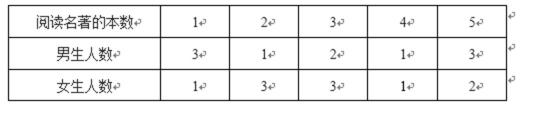
某班倡议假期每位学生至少阅读一本名著,为了解学生的阅读情况,对该班所有学生进行了调查.调查结果如下:
19.试根据上述数据,求这个班级女生阅读名著的平均本数;
20.若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率;
21.试判断该班男生阅读名著本数的方差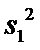
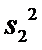

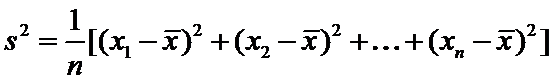
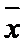
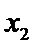
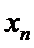
正确答案
3本;
解析
试题分析:本题属常见的统计类问题,在审题时一要会识图,二要认真列出基本事件再下手去做。题目较简单,主要是题意的理解。
(Ⅰ)女生阅读名著的平均本数
考查方向
解题思路
本题考查统计的相关知识和概率的计算,解题步骤如下:
由频数分布表分析数据,求出平均数即可。
根据题意列出基本事件完成概率的计算,再根据方差的计算公式完成第三问。
易错点
此题难度不大,主要是题意的理解,数据的计算,属于送分题。
正确答案
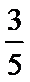
解析
试题分析:本题属常见的统计类问题,在审题时一要会识图,二要认真列出基本事件再下手去做。题目较简单,主要是题意的理解。
(Ⅱ)设事件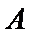
男生阅读5本名著的3人分别记为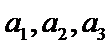
从阅读5本名著的5名学生中任取2人,共有10个结果,分别是:
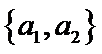
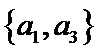
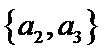
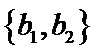
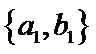
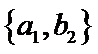
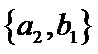
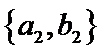
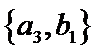
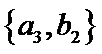
其中男生和女生各1人共有6个结果,分别是:
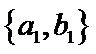
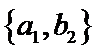
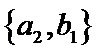
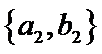
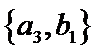
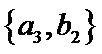
则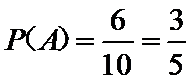
考查方向
解题思路
本题考查统计的相关知识和概率的计算,解题步骤如下:
由频数分布表分析数据,求出平均数即可。
根据题意列出基本事件完成概率的计算,再根据方差的计算公式完成第三问。
易错点
此题难度不大,主要是题意的理解,数据的计算,属于送分题。
正确答案
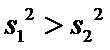
解析
试题分析:本题属常见的统计类问题,在审题时一要会识图,二要认真列出基本事件再下手去做。题目较简单,主要是题意的理解。
(Ⅱ)设事件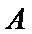
男生阅读5本名著的3人分别记为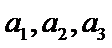
从阅读5本名著的5名学生中任取2人,共有10个结果,分别是:
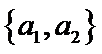
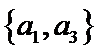
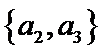
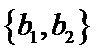
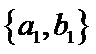
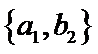
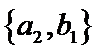
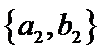
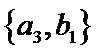
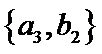
其中男生和女生各1人共有6个结果,分别是:
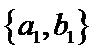
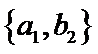
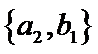
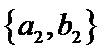
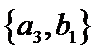
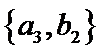
则
(Ⅲ)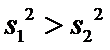
考查方向
解题思路
本题考查统计的相关知识和概率的计算,解题步骤如下:
由频数分布表分析数据,求出平均数即可。
根据题意列出基本事件完成概率的计算,再根据方差的计算公式完成第三问。
易错点
此题难度不大,主要是题意的理解,数据的计算,属于送分题。
已知椭圆

25.求以线段
26.过点







正确答案

解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“

(I)因为


所以以线段

考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:根据题意直接写出以线段


易错点
本题第二问在“

正确答案

解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“

则直线



等价于
依题意,直线


由

因为直线


即

设





令

当

所以
化简得,
所以
当
所以存在点

考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:根据题意直接写出以线段


易错点
本题第二问在“

已知函数
27.若



28.求函数
29.设



正确答案

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数求出切线方程;(2)对



(Ⅰ)若



则曲线


而



……………3分
考查方向
解题思路
本题考查导数的性质及其几何意义的应用,解题步骤如下:求出原函数的导函数,确定切线斜率再求出切线方程。对



易错点
第二问在对
第三问在研究区间
正确答案
函数



函数

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数求出切线方程;(2)对



(Ⅱ)函数


(1)当



令



令


所以当


所以函数


单调增区间为

(2)当



当



当




即当



(3)当

令







令


所以函数



函数

考查方向
解题思路
本题考查导数的性质及其几何意义的应用,解题步骤如下:求出原函数的导函数,确定切线斜率再求出切线方程。对



易错点
第二问在对
第三问在研究区间
正确答案
当


解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数求出切线方程;(2)对



(Ⅲ)(1)当


所以不存在极值点;
(2)当


在
若函数


解得

所以
综上所述,当


…………13分
考查方向
解题思路
本题考查导数的性质及其几何意义的应用,解题步骤如下:求出原函数的导函数,确定切线斜率再求出切线方程。对



易错点
第二问在对
第三问在研究区间
22.求证:平面

23.若



24.试判断直线

若能垂直,求
正确答案
略;
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线线垂直和面面平行关系才能下手去做;(2)第三问要注意理解和灵活运用

(Ⅰ)由已知,



又因为




因为


又
所以

又因为

所以平面

考查方向
解题思路
本题考查空间几何体中的面面垂直和线面平行的基本证明和计算,解题步骤如下:根据已知得出








易错点
第三问由


正确答案
略;
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线线垂直和面面平行关系才能下手去做;(2)第三问要注意理解和灵活运用

(Ⅱ)
取





由于



所以

则四边形

又



所以

由于



所以
又



所以
则
又



所以

由于


由于

所以

考查方向
解题思路
本题考查空间几何体中的面面垂直和线面平行的基本证明和计算,解题步骤如下:根据已知得出








易错点
第三问由


正确答案

解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线线垂直和面面平行关系才能下手去做;(2)第三问要注意理解和灵活运用

(III)假设

由

则
设

当

所以


由已知
所以

由于
因此直线

考查方向
解题思路
本题考查空间几何体中的面面垂直和线面平行的基本证明和计算,解题步骤如下:根据已知得出








易错点
第三问由