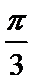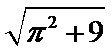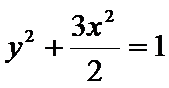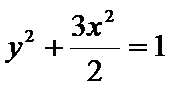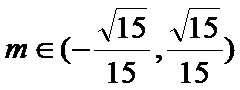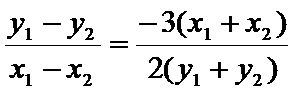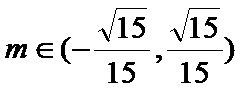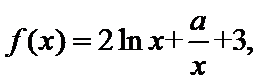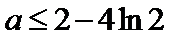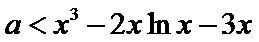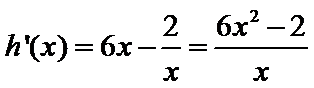- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合

正确答案
解析


考查方向
解题思路
求出集合A和集合B,然后运用集合的运算性质。
易错点
集合A表示的是不等式表示范围内的整数。
知识点
6.已知实数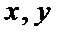
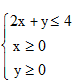
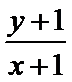
正确答案
解析
作出不等式组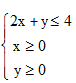
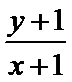
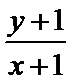
考查方向
解题思路
作出可行域,平行直线可得直线过点A(3,0)时,z取最大值,代值计算可得.
易错点
找不到什么时候取到最大值。
知识点
7.如果执行如图的程序框图,那么输出的值与下面第几次循环所得的结果一致( )。
正确答案
解析
由题意可知:第一次循环运算为:







考查方向
解题思路
先运行几次找到周期,然后利用周期性即可解出答案。
易错点
搞错循环。
知识点
8.已知



正确答案
解析


考查方向
解题思路
先根据垂直数量积为零求出未知参数m,再计算出b向量的模。
易错点
本题不知道向量垂直坐标满足的关系式。
知识点
9.一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的体积为( )
正确答案
解析
此几何体是三棱锥P-ABC(直观图如右图),底面是斜边长为4的等腰直角三角形ACB,且顶点在底面内的射影D是底面直角三角形斜边AB的中点.易知,三棱锥P-ABC的外接球的球心O在PD上.
设球O的半径为r,则


∴外接球的表面积为
考查方向
解题思路
先将直观图还原出来,再计算球的半径进一步计算出球的表面积。
易错点
不会还原直观图。
知识点
2.复数
正确答案
解析


考查方向
解题思路
先分母实数化,再利用数代数形式的乘除运算。
易错点
不会分母实数化化简。
知识点
3.已知等差数列
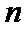
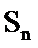
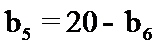
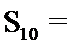
正确答案
解析
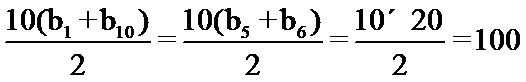
考查方向
解题思路
利用等差数列的求和公式表示出前10项的和,再利用等差数列的性质即可解出。
易错点
不会利用等差数列的性质来求解。
知识点
4.将函数f (x) =
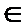
正确答案
解析
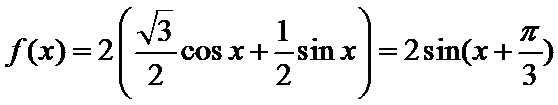
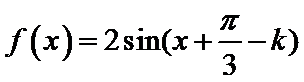
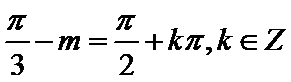
考查方向
解题思路
先利用辅助角公式合二为一,再利用三角函数的性质找出正确答案。
易错点
三角函数的性质。
知识点
5.某洗发水的广告费用x与销售额y的统计数据如下表所示,根据表中数据可得回归方程

正确答案
解析
由表中数据得:


从而线性回归方程为


由表中数据得:


从而线性回归方程为


考查方向
解题思路
根据回归直线方程过样本的中心点即可解出。
易错点
不知道考查的知识点是什么。
知识点
10.若椭圆






正确答案
解析
因为







考查方向
解题思路
用设而不求的方法来做。
易错点
不会用设而不求的方法来做。
知识点
12.已知定义在实数集







正确答案
解析
构造函数













考查方向
解题思路
构造函数再利用已知条件即可解出。
易错点
不会构造函数求解。
知识点
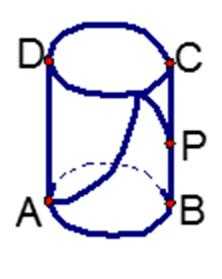
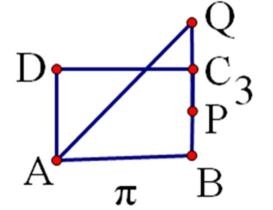
11. 如图,有一圆柱开口容器(下表面封闭),其轴截面是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒的所经过的最短路程是( )
正确答案
解析
如图,展开后作辅助线,使得QC=CP,则AQ即为所求最小距离,利用勾股定理可得D选项是正确的。
考查方向
解题思路
将图像展开之后,通过等价转化,最后变成两点间的距离来求解。
易错点
不知道怎样将圆柱展开。。
知识点
14.定义在[-2,2]上的偶函数f(x)在[-2,0]上为增,若满足f(1-m) <f(m),则m的取值范围是________________。
正确答案
解析
由已知再结合偶函数的性质可知在[0,2]上单调递减,所以满足

考查方向
解题思路
利用函数的奇偶性找到对称的定义域上函数的单调性,然后利用函数的单调性得到一个不等式,再结合函数的定义域,解一个不等式组即可。
易错点
本题容易忽视函数的定义域。。
知识点
13.函数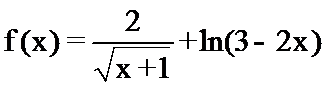
正确答案
解析
由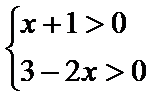
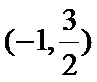
考查方向
解题思路
分别求出使得函数有意义的x的取值范围。
易错点
分母不可以为0忘记。
知识点
15.已知正数


正确答案
10
解析


考查方向
解题思路
本题考查基本不等式的求最值应用,解题步骤如下:将要求的表达式乘以x+y然后化简后利用基本不等式即可解出。
易错点
本题不会将9用x+y代入求解。。
知识点
16.函数

正确答案
解析
因为







考查方向
解题思路
先求导,再利用基本不等式来求解。
易错点
导数的几何意义不清楚。
知识点
如图所示,茎叶图记录了甲乙两组歌手在参加“我是歌手”这个节目是演唱得分情况。乙组某个数据模糊,记为k,已知甲、乙两组的平均成绩相同.
19.求k的值,并分别求出他们的方差;
20.在甲、乙两组中各抽出一名歌手,求这两名歌手的得分之和不低于12分的概率.
正确答案
甲
解析
(1)

又
考查方向
解题思路
由甲乙平均成绩相等可求
易错点
不知道方差的公式。
正确答案

解析
设甲组的4名歌手分别ABCD,乙组的4名歌手分别为EFGH,从2组中分别抽一个歌手出来共有16个基本事件,得分之和低于12分的包含2个基本事件,由古典概型的概率公式可以得两名歌手的得分之和不低于12分的概率为
考查方向
解题思路
列出所有基本事件,用符合条件的基本事件的个数除以基本事件的总数即可.
易错点
不会求解未知数导致后面做不出来。
在△ABC中,角A,B,C的对边分别是a,b,c,满足b2+c2=bc+a2.
17.求角A的大小;
18.已知等差数列{an}的公差不为零,若a1cosA=1,且a2,a4,a8成等比数列,求
正确答案
解析
∵△ABC中,b2+c2=a2-bc
∴根据余弦定理,得cosA=
∵A∈(0,π),∴A=
考查方向
解题思路
根据题中等式,结合余弦定理算出cosA=

易错点
不能根据已经条件结合余弦定理来做。
正确答案
解析
设数列{





∴



∴Sn=(1-








考查方向
解题思路
由(1)及条件a1cosA=1可求出




易错点
不会将数列裂项来求和。
已知四棱锥





21.求证:
22.求二面角
正确答案
证明:在直角梯形














解析
(1)证明:在直角梯形














考查方向
解题思路
由线线到线面的平行。
易错点
定理的条件写不全。
正确答案
解析
(2)取














由







考查方向
解题思路
先作出线面角再通过解三角形即可。
易错点
不会做出线面角。
已知椭圆的中心在坐标原点,以椭圆中的a,b,c为边可以构成一个三角形ABC,且在三角形ABC中满足一个等式
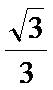
23.求椭圆的方程;
24.若椭圆上存在不同两点关于直线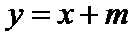
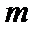
正确答案
解析
(1)设椭圆的方程为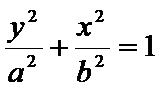

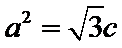
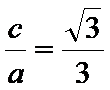
从而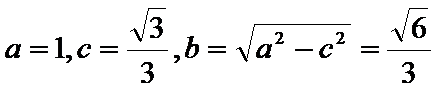
所以椭圆的方程为
考查方向
解题思路
根据已知条件构造方程组解出即可。
易错点
不知道准线怎么转化。
正确答案
解析
(2)设椭圆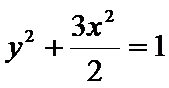
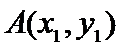
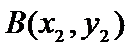
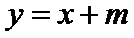
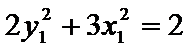
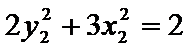
两式相减整理得
设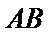
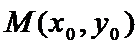
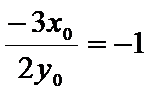
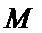
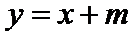
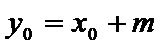
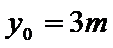
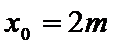
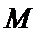
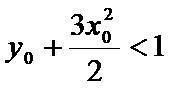
即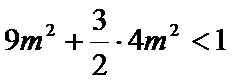
考查方向
解题思路
根据步骤来计算。
易错点
不会用设而不求的方法来求解。
考生在第22、23、24题中任选一道作答,并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂的首题进行评分.
22.【选修4—1】几何证明选讲(请回答27、28题)
如图,在






23.【选修4—4】极坐标与参数方程(请回答29、30题)
在直角坐标系







24.【选修4—5】不等式选讲(请回答31、32题)
已知
27.求证:
28.求线段
29.化

30.若








31.求不等式
32.设


正确答案
证明:由已知




解析
(Ⅰ)证明:由已知




考查方向
解题思路
由割线定理求解。
易错点
不会利用切割线定理来解答。。
正确答案

解析
(Ⅱ)解:如图,过点






同理

①+②得
即
所以


考查方向
解题思路
由割线定理求解。
易错点
不记得定理。
正确答案
(Ⅰ)







解析
(Ⅰ)







考查方向
解题思路
参数方程化为普通方程。
易错点
极坐标转不会化为直角坐标,参数方程不会转化为普通方程。
正确答案
解析
(Ⅱ)当

设





从而当

考查方向
解题思路
极坐标方程化为直角坐标中的方程再利用点到直线的距离公式再结合三角函数即可。
易错点
不知道参数的几何意义。
正确答案
解析
(Ⅰ)解:不等式


所以不等式
考查方向
解题思路
去掉绝对值分类讨论求解。
易错点
不会去掉绝对值。
正确答案
因为
因为


同理:

所以
所以
解析
证明:因为
因为


同理:

所以
所以
考查方向
解题思路
利用基本不等式来解决.
易错点
不会利用基本不等式处理。。
函数
25.当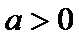
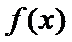
26.若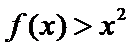
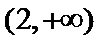
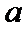
正确答案
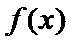
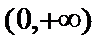
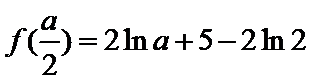
解析
(1)由题意: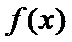
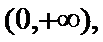
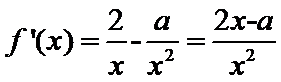
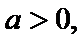
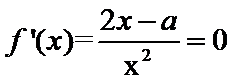
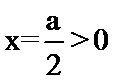
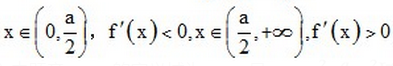
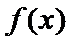
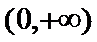
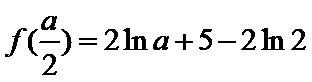
考查方向
解题思路
先求导再判断导数的符号。
易错点
求导弄错。
正确答案
解析
(2)因为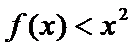
又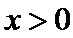
令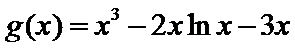
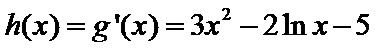
因为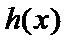
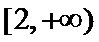
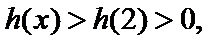
所以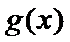
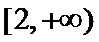
令
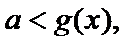
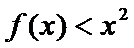
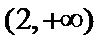
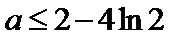
考查方向
解题思路
构造函数再利用导数这个工具即可解出。
易错点
不会构造函数去求解。