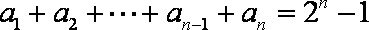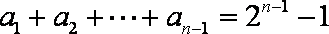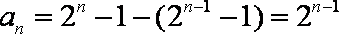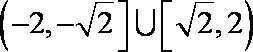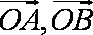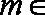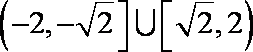- 真题试卷
- 模拟试卷
- 预测试卷
2.已知复数 
正确答案
解析
∵z=

∴

知识点
3.设非零向量 



正确答案
解析
设













知识点
9.已知函数

正确答案
解析
∵f(x)=

∴f(﹣x)=1﹣
∴f(x)+f(﹣x)=2;
∵f(a)=
∴f(﹣a)=2﹣f(a)=2﹣

故选C.
知识点
6.在数列

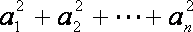
正确答案
解析


①-②得:

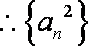
则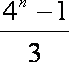
故选:D
知识点
4.一个几何体的三视图如图所示,则该几何体的体积是
正确答案
解析
该几何体是两个全等的斜四棱柱对接而成的几何体,其中每个四棱柱是底面邻边长分别为3, 2的长方形,高为1,所以该几何体的体积为:
知识点
7.已知函数
正确答案
解析
由题意可知f(x)的定义域为R.
∵
∴f(﹣x)+f(x)=
=
又f(x)=

∴f(x﹣2)+f(x2﹣4)<0可化为f(x﹣2)<﹣f(x2﹣4)
即f(x﹣2)<f(4﹣x2),可得x﹣2<4﹣x2,即x2+x﹣6<0,解得﹣3<x<2,
故选D。
知识点
1.集合P={3,4,5},Q={6,7},定义

正确答案
解析


知识点
5.已知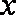
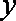
已求得关于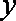

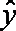
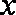
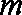
正确答案
解析

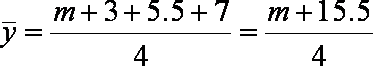
因为回归直线过点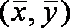
所以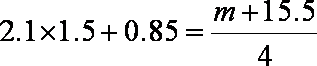
解得:
故选:D
知识点
8.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<

正确答案
解析
由题意可得

y=sin[2(x﹣



故函数f(x)=sin(2x﹣




故选:D.
知识点
10.在△ABC中,若|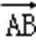

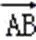
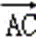

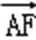
正确答案
解析
若|
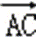
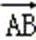
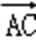
则
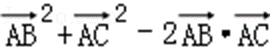
即有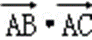
E,F为BC边的三等分点,
则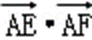
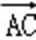
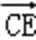

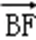

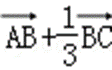
=(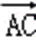
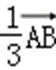


=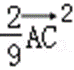
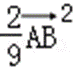
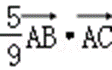
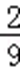

故选B.
知识点
11.假设在5秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于2秒,手机就会受到干扰,则手机受到干扰的概率为
正确答案
解析
分别设两个互相独立的短信收到的时间为x,y.则所有事件集可表示为0≤x≤5,0≤y≤5。由题目得,如果手机受则到干扰的事件发生,必有|x﹣y|≤2。三个不等式联立,则该事件即为x﹣y=2和y﹣x=2在0≤x≤5,0≤y≤5的正方形中围起来的图形:
即图中阴影区域而所有事件的集合即为正方型面积52=25,
阴影部分的面积25﹣2×
所以阴影区域面积和正方形面积比值即为手机受到干扰的概率为
故选:D。
知识点
12.若存在正实数




①



其中“在
正确答案
解析
①
②





③




知识点
13.设Sn为等比数列{an}的前n项和,8a2-a5=0 则
正确答案
5
解析
由8a2-a5=0得公比q=2,所以
知识点
15.己知直线x+ y+m=0与圆x2+ y2 =2交于不同的两点A、B,O是坐标原点,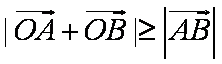
正确答案
解析
因为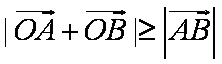
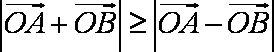


夹角


知识点
16.已知函数f(x)周期为4,且当x∈(﹣1,3]时,f(x)=
正确答案

解析
∵当x∈(﹣1,1]时,将函数化为方程x2+
∴实质上为一个半椭圆,其图象如图所示,
同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,
由图易知直线 y=

而与第三个半椭圆(x﹣8)2+
将 y=

则(t+1)x2﹣8tx+15t=0,由△=(8t)2﹣4×15t (t+1)>0,得t>15,由9m2>15,且m>0得 m 
同样由 y=


三棱锥

知识点
14.已知如图所示的矩形,长为12,宽为5,在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为600颗,则可以估计阴影部分的面积约为 。
正确答案
36
解析
可以估计阴影部分的面积约为:
知识点
19.四棱锥






(1)求证:
(2)求证:
(3)求三棱锥
正确答案
见解析。
解析
(1)取

又



又四边形




所以,

所以,
(2)
所以,


由 ①②可知,
(3)取


又
又因为,

所以,



即
所以
知识点
18.某校从参加某次知识竞赛的同学中,选取






(1)求分数在
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率。
正确答案
(1)

解析
(1)分数在[70,80)内的频率为1﹣(0.010+0.015+0.015+0.025+0.005)×10=0.3,
∴小矩形的高为0.030,补全频率分布直方图如图:
(2)由频率频率分布直方图知前三组的频率之和为0.1+0.15+0.15=0.4,
∴中位数在第四组,设中位数为70+x,则0.4+0.030×x=0.5⇒x=
∴数据的中位数为70+

(3)第1组:
第6组:
共有36个基本事件,满足条件的有18个,所以概率为
知识点
21.已知函数
(1)若
(2)若函数在
正确答案
(1)当

(2)
解析
(1)显然函数定义域为(0,+
令
当
当
(2)
令
当
当
故当

知识点
17.在



(1)求角A的值,
(2)若
正确答案
(1)
解析
(1)由

即
所以


(2)

因为

所以
即

知识点
22.如图,四边形







(1)求
(2)若



正确答案
见解析。
解析
(1)由



设

所以
(2)
知识点
20.已知椭圆







(1)求椭圆
(2)过定点












正确答案
见解析。
解析
(1)由已知



在


故

于是椭圆

(2)设




假设存在点






因为


因为


整理得
因为