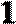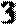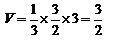2015年高考权威预测卷文科数学 (全国新课标卷II)

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

4.某同学同时抛掷两颗骰子，得到的点数分别记为、b，则双曲线的离心率的概率是（）

正确答案

解析

由得 b>2a 若a=1则b=3、4、5、6，若a=2则b=5、6 P=

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

1.集合A={x|y=}，B={y|y=log2x，x＞0}，则A∩B等于（　　）

B∅

C[0，+∞）

D（0，+∞）

正确答案

解析

集合A={x|y=}={x|x≥0}，集合B={y|y=log2x，x＞0}=R，因为A⊆B，所以A∩B=A={x|x≥0}，故选：C.

知识点

集合的含义

题型：单选题

分值: 5分

5.下列函数中，既是偶函数，又在区间(0，3)内是增函数的是（）

Ay=

By=cosx

Cy=

Dy=x＋x－1

正确答案

解析

故函数为偶函数，故函数在（0,3）为增函数，故A正确；y=cosx 和y=x＋x－1奇函数，故B，D错；y=为偶函数，但是在(0，3)内是减函数.

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6.设等边三角形ABC边长为6，若，则等于（）

C- 18

D18

正确答案

解析

由题意可得

知识点

任意角的概念

题型：单选题

分值: 5分

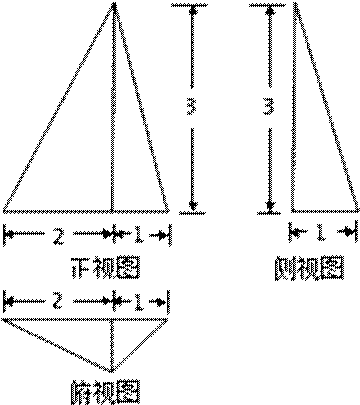
9.已知某几何体的三视图如上图所示，则该几何体的体积为 ( )

正确答案

解析

由三视图易知，该几何体是底面积为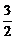，高为3的三棱锥，由锥体的体积公式得

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

10.已知变量满足约束条件若恒成立，则实数的取值范围为( )

A(∞,1]

B[1,+∞)

C[1,1]

D[-1,1)

正确答案

解析

由题意作出其平面区域，

则x+2y≥﹣5恒成立可化为图象中的阴影部分在直线x+2y=﹣5的上方，

则实数a的取值范围为[﹣1，1]．

故答案为：[﹣1，1]．

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

2.若角的终边过点，则的值为（）

正确答案

解析

因为角的终边过点，所以，

所以故选B.

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

3.已知i为虚数单位，复数，则复数z的实部为（　　）

正确答案

解析

复数===﹣，则复数z的实部为﹣．

故选：D.

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

7.如图，网格纸上小正方形的边长为，粗线画出的是某多面体的三视图，则该多面体的体积为（）

正确答案

解析

由三视图可知，该多面体是一个四棱锥，且由一个顶点出发的三条侧棱两两垂直，长度都为4， ∴其体积为

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

8.已知函数的图象与轴的两个相邻交点的距离等于，若将函数的图象向左平移个单位得到函数的图象，则是减函数的区间为（）

正确答案

解析

因为=，由图象与轴的两个相邻交点的距离等于，所以其最小正周期为π，则，所以，对于A,B,C,D四个选项对应的2x的范围分别是，所以应选D.

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

11.已知F是抛物线y2=x的焦点，A，B是该抛物线上的两点，|AF|+|BF|=3，则线段AB的中点到y轴的距离为（　　）

正确答案

解析

∵F是抛物线y2=x的焦点，

F（）准线方程x=，

设A（x1，y1），B（x2，y2），

根据抛物线的定义抛物线上的点到焦点的距离等于到准线的距离|AF|=，|BF|=，

∴|AF|+|BF|==3

解得，

∴线段AB的中点横坐标为，

∴线段AB的中点到y轴的距离为．

故选C.

知识点

抛物线的定义及应用

题型：单选题

分值: 5分

12.已知函数，(>0，其中为自然对数的底数)，若关于的方程，有且只有一个实数解，则实数的取值范围为（）

正确答案

解析

若a=0则方程f（f（x））=0有无数个实根，不满足条件,

若a≠0，若f（f（x））=0，则f（x）=1，∵x＞0时，f（）=1，

关于x的方程f（f（x））=0有且只有一个实数解，
故当x≤0时，a•ex=1无解，即ex=在x≤0时无解，

故＜0或＞1，故a∈（-∞，0）∪（0，1）

知识点

函数的概念及其构成要素

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

14.正四面体的棱长为4，为棱的中点，过作其外接球的截面，则截面面积的最小值为______．

正确答案

解析

将四面体ABCD放置于正方体中，如图所示

可得正方体的外接球就是四面体ABCD的外接球，

∵正四面体ABCD的棱长为4，

∴正方体的棱长为

可得外接球半径R满足2R＝解得R=

E为棱BC的中点，过E作其外接球的截面，当截面到球心O的距离最大时，

截面圆的面积达最小值，

此时球心O到截面的距离等于正方体棱长的一半，

可得截面圆的半径为r=

得到截面圆的面积最小值为S= =4π．

故答案为：4π

知识点

空间几何体的结构特征

题型：填空题

分值: 5分

15.设函数则满足f(x)≤2的x的取值范围是________．

正确答案

解析

由得，由得

，所以x的取值范围是

【思路点拨】利用同底法求解指数、对数不等式.

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

13.已知直线与圆交于两点，是坐标原点，向量满足，则实数的值是。

正确答案

±2

解析

因为向量满足，所以OA⊥OB，又直线x+y=a的斜率为－1，所以直线经过圆与y轴的交点，所以a=±2.

【思路点拨】本题先由向量加法与减法的几何意义得到OA⊥OB，再由所给直线与圆的特殊性确定实数a的值.

知识点

空间几何体的结构特征

题型：填空题

分值: 5分

16.如图所示，我舰在敌岛A南偏西50°相距12海里的B处，发现敌舰正由岛A沿北偏西10°的方向以每小时10海里的速度航行，我舰要用2小时在C处追上敌舰，则需要的速度是_______________.

正确答案

解析

略

知识点

函数的概念及其构成要素

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

20.如图，已知圆是椭圆的内接的内切圆，其中为椭圆的左顶点.

（1）求圆的半径；

（2）过点作圆的两条切线交椭圆于，两点，证明：直线与圆相切.

正确答案

见解析。

解析

（1）设，过圆心作于，交长轴于

由得，

即 ①

而点在椭圆上，

②

由①、②式得，

解得或（舍去）

（2）设过点与圆相切的直线方程为： ③

则，即 ④

解得

将③代入得，

则异于零的解为

设，则

则直线的斜率为：

于是直线的方程为：即

则圆心（2，0）到直线的距离故结论成立.

知识点

椭圆的定义及标准方程

题型：简答题

分值: 12分

17.在等比数列中，

（1）求数列的通项公式；

（2）令求数列的前项和

正确答案

（1）

（2）

解析

（1）设等比数列的公比为依题意得解得

所以：数列的通项公式

（2）由（1）得

知识点

任意角的概念

题型：简答题

分值: 12分

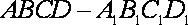
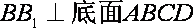
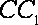
18.如图，已知四棱柱的底面是菱形，侧棱,E是侧棱的中点.

（1）求证：；

（2）求证：AC∥平面.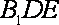

正确答案

见解析。

解析

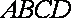
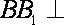
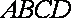
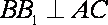
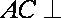
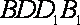
（1）因为底面是菱形，所以,因为底面，所以，所以

平面.

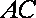
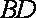
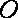
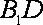
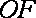
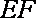
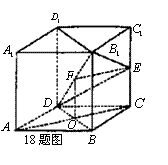
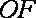
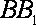
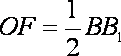
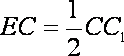
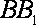
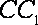
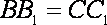
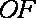
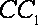
（2）设，交于点,取的中点,连接,,

则∥，且，又，

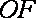
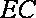
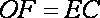
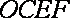
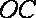
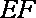
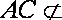
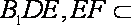
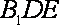
∥，，所以∥，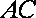

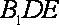
且，所以∥，且

,所以四边形为平行四边形，

∥，又平面平面，

所以∥平面.

知识点

空间几何体的结构特征

题型：简答题

分值: 12分

19.在某学校组织的一次篮球总投篮训练中，规定每人最多投3次；在处每投进一球得3分，在处每投进一球得2分，如果前两次得分之和超过3分即停止投篮，否则投第3次。某同学在处的命中率为0.25，在处的命中率为。该同学选择先在处投一球，以后都在处投，用表示该同学投篮的训练结束后所得的总分，其分布列为

（1）求的值；

（2）求随机变量的数学期望；

（3）试比较该同学选择在处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。

正确答案

见解析。

解析

（1）由题设知，“”对应的事件为“在三次投篮中没有一次投中”，由对立事件和相互独立事件性质可知解得

（2）根据题意

因此

（3）用表示事件“该同学选择第一次在处投，以后都在处投，得分超过3分”，用表示事件“该同学选择都在处投，得分超过3分”，

则

故

即该同学选择都在处投篮得分超过3分的概率大于该同学选择第一次在处投以后都在处投得分超过3分的概率。

知识点

随机事件的关系

题型：简答题

分值: 12分

21.已知二次函数设方程的两个实数根为和

（1）如果设函数的对称轴为求证：

（2）如果求b的取值范围。

正确答案

见解析。

解析

（1）由及可得即即两式相加得

（2）由可得又同号。

等价于或

即或解之得或

知识点

函数的概念及其构成要素

题型：简答题

分值: 10分

22.如图，在中，以为直径的交于点，过作，垂足为，连接交于点.求证：BE·CE=EF·EA

正确答案

见解析。

解析

解析：因为中，

所以所以为的切线.

所以

连接，因为,所以

所以

在四边形中，

所以为矩形.

所以即

所以BE·CE=EF·EA

知识点

直线的倾斜角与斜率

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷