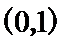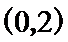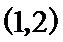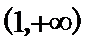- 真题试卷
- 模拟试卷
- 预测试卷
3.函数f(x)在R上可导,那么 f(x) 是奇函数的必要非充分条件是( )
正确答案
解析
先判断选项推出题目条件的是AB,所以这两个选项排除,然后C选项不满足必要性,所以选D
考查方向
解题思路
首先必要性满足的是题目条件能推出选项,然后满足选项推不出题目条件
易错点
没注意必要非充分条件是谁推出谁
知识点
8.如图所示的程序框图中,要使S输出的值为120,则条件①应该为 ( )
正确答案
解析
经检验当循环体被执行4次后s的值已经达到120.
考查方向
解题思路
用循环的步骤去检验
易错点
循环条件的设定
知识点
9.已知x,y满足条件
正确答案
解析
先画可行域,令y-3x=z得直线l的方程为y=3x +z,其中z是直线l的纵截距,改变z就在平移该直线,显然过点(-1,1)时得最大值4,直线可以无限向右平移所以z无最小值
考查方向
解题思路
做可行域(如图)作然后作目标函数的直线,平移得到最值解
易错点
没看清开放域,容易出现最值解位置的错误。
知识点
10. 在边长为2的正三角形ABC中,D为BC中点,点P是该等边三角形的三边上的动点,求
正确答案
解析
设AD的中点为O,那么

考查方向
解题思路
本题可以建立坐标系用向量建立函数关系,可以直接用向量点积的几何意义建立函数关系求解
易错点
容易选择D答案,选择两个端点检验。
知识点
1.已知集合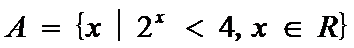
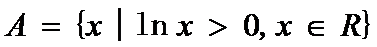

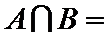
正确答案
解析
因为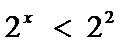
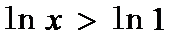
考查方向
解题思路
求出集合A和集合B,然后运用集合的运算性质。
易错点
集合B中对数函数的定义域和ln1=0。
知识点
2.若复数
正确答案
解析
考查方向
解题思路
先运算化简,再判断
易错点
虚部的概念不清楚
知识点
4.设向量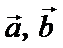
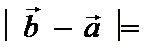
正确答案
解析

考查方向
解题思路
先使用向量减法的几何意义做
易错点
没理解向量模的 意义
知识点
5.已知等比数列



正确答案
解析
先用等比数列性质求出a5=2,然后根据
考查方向
解题思路
先用等比数列性质求出a5再用等比关系求和,
易错点
搞不清新等比数列的公比
知识点
6.已知某正四棱柱被一个平面截取一部分所剩下的几何体三视图如下图所示,则剩下的部分与原正四棱柱的体积之比为 ( )
正确答案
解析
先确认切掉的是左前方的一个角,这个角与正四棱柱等高且底面积是正四棱柱底面积的一半,所以切掉部分是整体的1/6,因此答案为5/6
考查方向
解题思路
先确认切掉的是左前方的一个角,再算体积
易错点
没有识别出切掉的刚好是一个角
知识点
7.已知圆心为(2,0)的圆C与直线y=x相切,求切点到原点的距离 ( )
正确答案
解析
先画图由相切得圆心到直线的距离就是半径长,再用勾股定理计算出切点到原点的距离为
考查方向
解题思路
由相切求出半径长,再用勾股定理计算
易错点
相切关系的刻画
知识点
12.已知正方体ABCD-A1B1C1D1 ,以点A为球心半径为x作球,球面与正方体各棱交点构成的平面图形的面积为y,那么y与x的函数关系对应的图像为( )
正确答案
解析
前面和后面是线性的CD被排除,又由于中间段保持不变,所以选A
考查方向
解题思路
先分成三种情形讨论:等边三角形、六边形和等边三角形
易错点
无法确定平面的形状
知识点
11.若函数
正确答案
解析



考查方向
解题思路
先求出导函数,根据零点存在定理求出在(-1,2)上有极值点时k的范围,再取补集
易错点
区间(-1,2)上没有极值点误解为有极值点
知识点
已知AB为圆O的直径,C是圆上一点,V为圆O所在平面外一点,VA=VB=VC,E为AC中点.
19.求证:直线OE//平面VBC
20.求证:
正确答案
(Ⅰ) 因为O、E分别为AB、AE的中点
所以OE//BC
因为OE不在平面VBC上,BC在平面VBC上
所以直线OE//平面VBC
解析
(Ⅰ) 因为O、E分别为AB、AE的中点
所以OE//BC
因为OE不在平面VBC上,BC在平面VBC上
所以直线OE//平面VBC
考查方向
解题思路
用中位线证明
易错点
面面垂直的垂线找不到
正确答案
因为VA=VB=VC,OB=OA=OC
VO为公共边
∴ △VOA≌△VOC;
∴ ∠V0A=∠VOC=90o. ∴ VO⊥OC;



∴ VO⊥平面ABC.





因为VO







解析
因为VA=VB=VC,OB=OA=OC
VO为公共边
∴ △VOA≌△VOC;
∴ ∠V0A=∠VOC=90o. ∴ VO⊥OC;



∴ VO⊥平面ABC.





因为VO







考查方向
解题思路
(1)用中位线证明(2)找到并证明AC是平面VOE的垂线
易错点
面面垂直的垂线找不到
某市调研机构对该市教师工资应该什么水平进行民意调查,随机调查了50名,他们赞成的教师月收入频数、频率和其中被调查者是老师的频数如下表:
21.若所抽调的50名市民中,赞成教师工资在[45,55)的有15名,求
22.若从收入(单位:百元)在[65,75)的被调查者中随机选取两人进行追踪调查,求选中的2人至少有1人不是老师的概率.
正确答案

解析
(I)由频率分布表得
即
因为所抽调的50名市民中,赞成教师收入(单位:百元)在[45,55)的有15名,
所以
所以
所以
且频率分布直方图如下:
考查方向
解题思路
(1)算出各自的频率与组距的比值
易错点
容易搞不清被调查的人是老师的人数。
正确答案
解析
设收入(单位:百元)在[65,75)的被调查者中是老师的分别是

事件
则从收入(单位:百元)在[65,75)的被调查者中,任选2名的基本事件共有10个:




事件




所以
故所求概率为
考查方向
解题思路
分类列举表示
易错点
容易搞不清被调查的人是老师的人数。
已知四边形ABCD为平行四边形,该四边形的面积为20,CD×cos∠DCA=3,AD×sin∠DAC=4..
17.求DC的长;
18.求四边形ABCD的周长.
正确答案
DC=5
解析
先解三角形ACD,求出边DC=5
考查方向
解题思路
先解三角形ACD再根据面积求边长
易错点
容易忽略条件在
正确答案
周长等于4+4
解析
根据面积求出AC=5,再根据余弦定理或面积公式得AD=2
考查方向
解题思路
先解三角形ACD再根据面积求边长
易错点
三角形。
已知椭圆C:

23.求椭圆C的离心率;
24.若M为椭圆上一点,求
正确答案
e=
解析
先两点代入得a=2和b=1,c=
考查方向
解题思路
先两点代入求出a和b ,再求c与e
易错点
代点解方程
正确答案
解析
设点M为(m,n)那么 


考查方向
解题思路
先两点代入求出a和b ,再求c;建立面积的函数表达式用函数求解最大值,也可以用直线与椭圆相切来做
易错点
三角形面积的底边选取与高的计算
已知函数
25.求
26.若方程
正确答案
切线方程为y=x
解析
所以切线方程为y=x
考查方向
解题思路
先求出导函数再确定单调性,根据草图求解
易错点
不能正确用导数确定函数的单调性与范围。
正确答案
方程
解析

所以f(x)在(

得f(x)的图像为
所以方程
考查方向
解题思路
先求出导函数再确定单调性,根据草图求解
易错点
不能正确用导数确定函数的单调性与范围。
请考生在以下3题中任选一题作答,则按所做的第一题计分,作答时请写清题号
【选修4-1】几何证明选讲(请回答27、28题)
四边形ABCD内接于圆O且AD与BC的延长线交于点E,FC为圆O的切线其中O为切点,AD=4,DF=FE=1,CD=2。
【选修4-4】坐标系与参数方程(请回答29、30题)
已知圆C的极坐标方程为



【选修4-5】不等式选讲(请回答31、32题)
已知c>0,
27.求FC和EC的长
28.求AB的长
29.求出圆C的圆心直角坐标
30.求直线l与圆C相交所得弦长的取值范围
31.求证:
32.求证:
正确答案
FC=
解析
(1)AD·FD=CD2得出CD·AF
再用勾股定理得FC=
考查方向
解题思路
用圆幂的相关定理联系关系
易错点
相似的比例关系不清楚
正确答案
AB=3
解析
(1)AD.FD=CD2得出CDAF
再用勾股定理得FC=
(2)ED.EA=EC.EB 得EB=3
再由(1)得ABBC
利用勾股定理得AB=3
考查方向
解题思路
用圆幂的相关定理联系关系
易错点
相似的比例关系不清楚
正确答案
(

解析
由极坐标的含义圆心为(

考查方向
解题思路
化为普通方程求解或直接运用极坐标的含义求解
易错点
极坐标方程认错,直线的参数误用
正确答案
[
解析
由直线的参数方程可以知道该直线过固定点(0,






所以弦长的取值范围是[
考查方向
解题思路
化为普通方程求解或直接运用极坐标的含义求解
易错点
极坐标方程认错,直线的参数误用
正确答案
因为c>0,
所以
所以
解析
因为c>0,
所以
所以
考查方向
解题思路
用综合法解决第一问,同时根据第一问的结论和绝对值性质解决第二问
易错点
没有用均值定理进行缩放
正确答案
由题目条件和(1)的结论知c〉b,从而
所以
解析
由题目条件和(1)的结论知c〉b,从而
所以
考查方向
解题思路
用综合法解决第一问,同时根据第一问的结论和绝对值性质解决第二问
易错点
没有用均值定理进行缩放或正确去绝对值
13.从甲、乙、丙、丁4名同学中随机选出3名同学参加志愿服务,其中甲没被入选的概率为
正确答案
1/4.
解析
4选3和4选一的个数相同。得甲没被入选的概率为1/4
考查方向
解题思路
先建立基本事件空间再数数。
易错点
无法数清基本事件。
知识点
16.已知数列



正确答案
6
解析


同理


考查方向
解题思路
先写出递推关系,再带入进行检验
易错点
弄错递推公式。
知识点
14.函数

正确答案
解析
化简得
考查方向
解题思路
再利用三角变换将函数化为一个角一个三角函数,再利用图像或性质
易错点
误用公式。
知识点
15. 已知双曲线

正确答案

解析
焦点到渐近线的距离为2得b=2,离心率说明是等轴双曲线,所以a=2,则左焦点为(-2
考查方向
解题思路
先求出双曲线方程,再求双曲线左焦点,最后求抛物线标准方程
易错点
离心率为