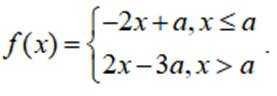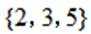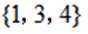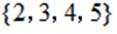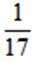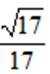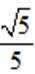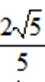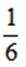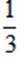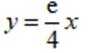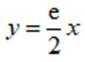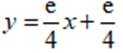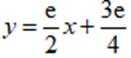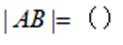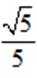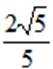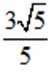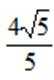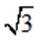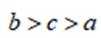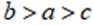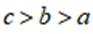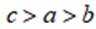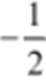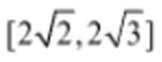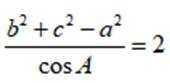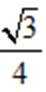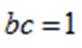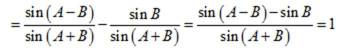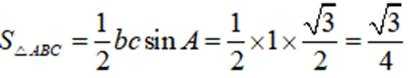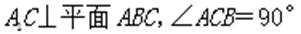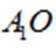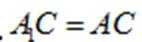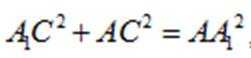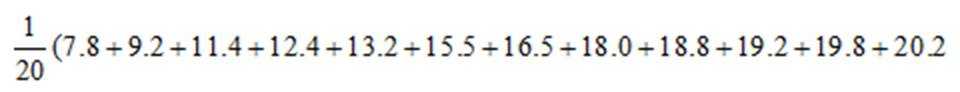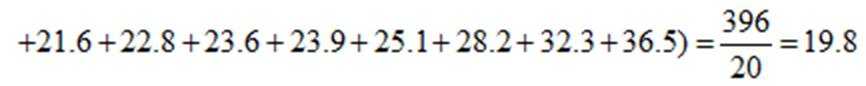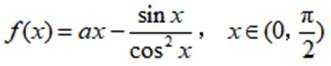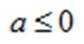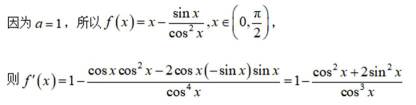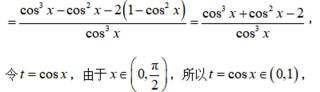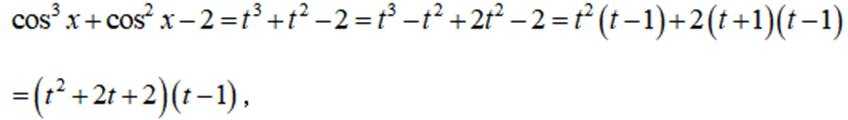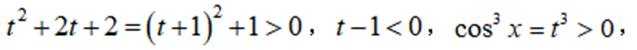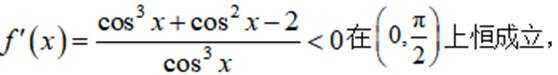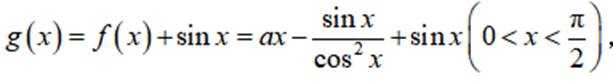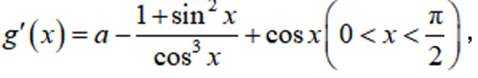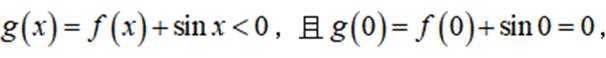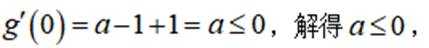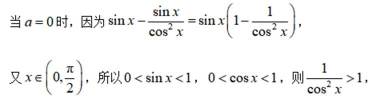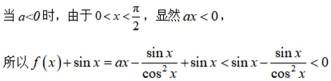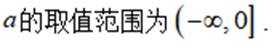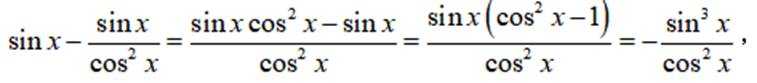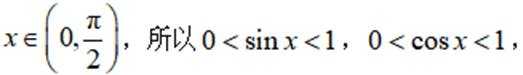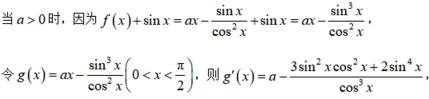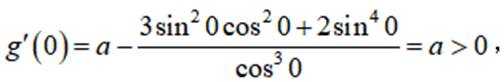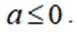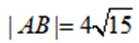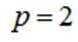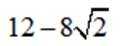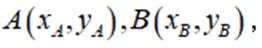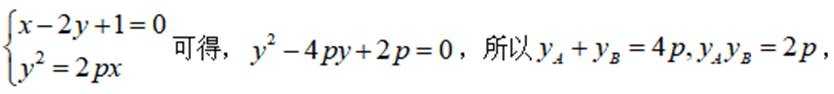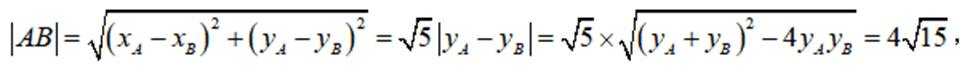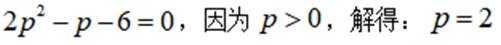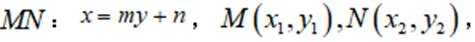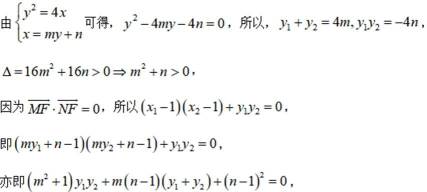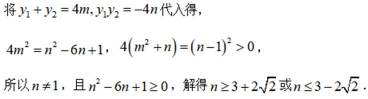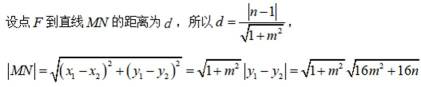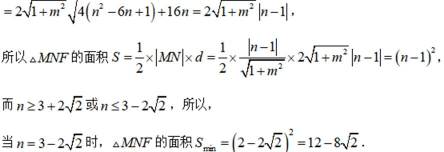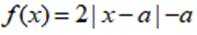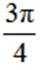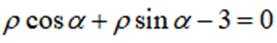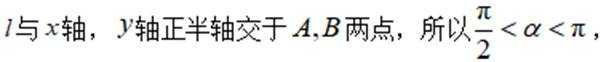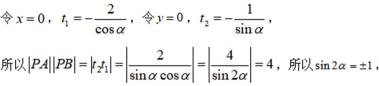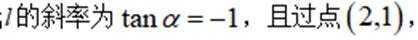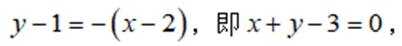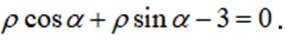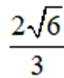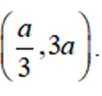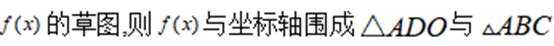- 真题试卷
- 模拟试卷
- 预测试卷
设全集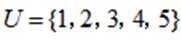
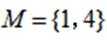
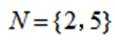
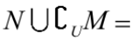
正确答案
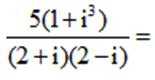
正确答案
已知向量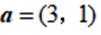
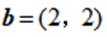
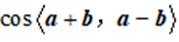
正确答案
某校文艺部有4名学生,其中高一、高二年级各2名,从这4名学生中随机选2名组织校文艺汇演,则这2名学生来自不同年级的概率为()
正确答案
记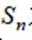
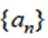
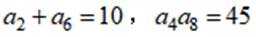
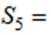
正确答案
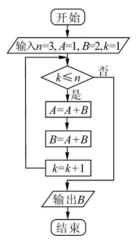
执行右边的程序框图,则输出的B=()
正确答案
设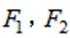
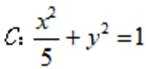

正确答案
曲线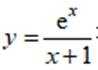
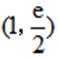
正确答案
已知双曲线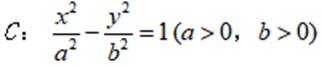
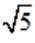
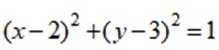
正确答案
在三棱锥P-ABC中,△ABC是边长为2的等边三角形,PA=PB=2,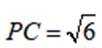
正确答案
已知函数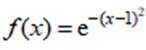
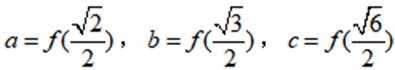
正确答案
函数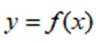
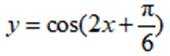
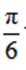
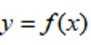
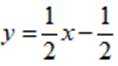
正确答案
记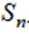
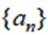
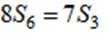
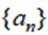
正确答案
若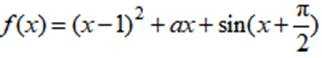
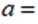
正确答案
2
若x,y满足约束条件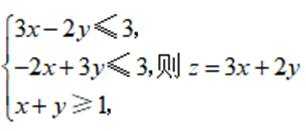
正确答案
15
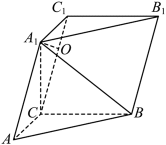
在正方体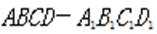
正确答案
记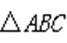
(1)求bc;
(2)若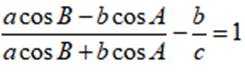
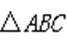
正确答案
(1)1 (2)
解析
(1)根据余弦定理即可解出;
(2)由(1)可知,只需求出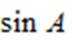
小问1详解
因为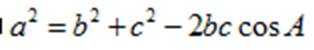
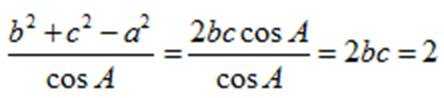
小问2详解
由正弦定理可得
变形可得: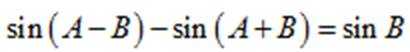
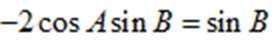
而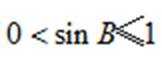
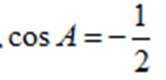
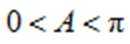
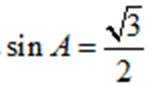
故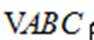
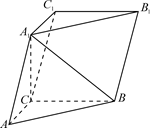
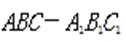
(1)证明: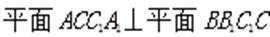
(2)设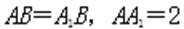
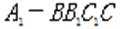
正确答案
(1)由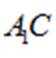
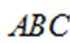
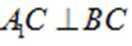
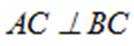
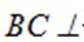

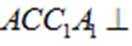
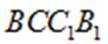
(2) 过点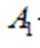
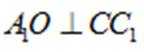
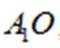
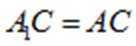
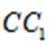
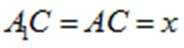
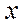
小问1详解
证明:因为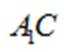
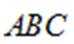
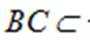
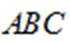
所以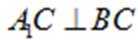
又因为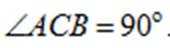
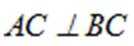
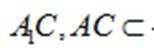
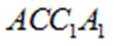
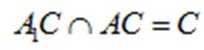
所以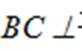
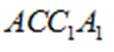
又因为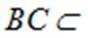
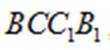
所以平面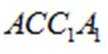
(2)1
如图,
过点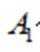
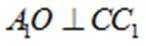
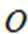
因为平面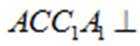
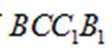
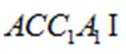
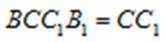
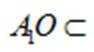
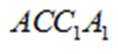
所以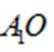
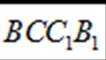
所以四棱锥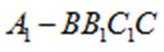
因为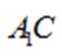
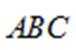
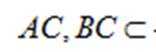
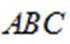
所以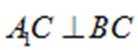
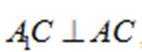
又因为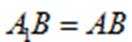
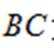
所以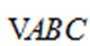
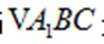
设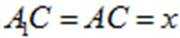
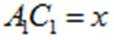
所以
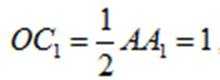
又因为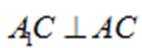
即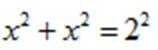
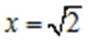
所以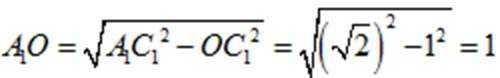
所以四棱锥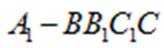
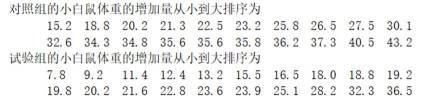
一项试验旨在研究臭氧效应,试验方案如下:选40只小白鼠,随机地将其中20只分配到试验组,另外20只分配到对照组,试验组的小白鼠饲养在高浓度臭氧环境,对照组的小白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位:g)试验结果如下:
(1)计算试验组的样本平均数;
(2)(ⅰ)求40只小白鼠体重的增加量的中位数m,再分别统计两样本中小于m与不小于m的数据的个数,完成如下列联表
(ⅱ)根据(i)中的列联表,能否有95%的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异?
附: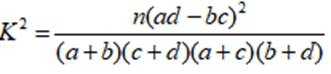
正确答案
(1)19.8
(2)(i)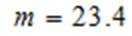
解析
(1)直接根据均值定义求解;
(2)(i)根据中位数的定义即可求得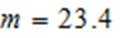
(ii)利用独立性检验的卡方计算进行检验,即可得解.
小问1详解
试验组样本平均数为:
小问2详解
(i)依题意,可知这40只小鼠体重的中位数是将两组数据合在一起,从小到大排后第20位与第21位数据的平均数,
由原数据可得第11位数据为18.8,后续依次为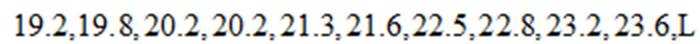
故第20位为23.2,第21位数据为23.6,
所以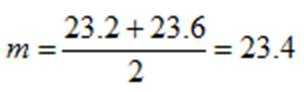
故列联表为:
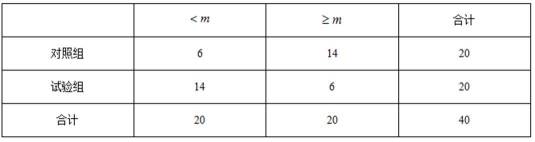
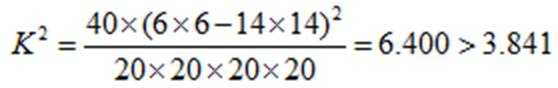
所以能有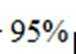
已知函数
(1)当a=1时,讨论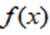
(2)若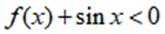
正确答案
(1)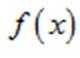
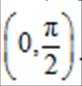
解析
(1)代入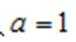
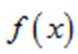
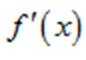
(2)法一:构造函数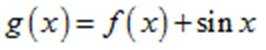
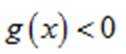
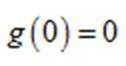
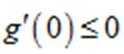
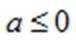
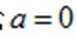
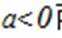
法二:先化简并判断得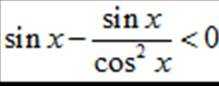
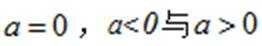
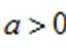
小问1详解
所以
因为
所以
所以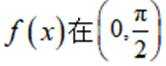
小问2详解
法一:
构建
则
若
则
所以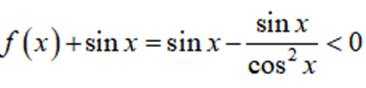
满足题意;
综上所述: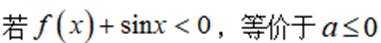
所以
法二:
因为
因为
故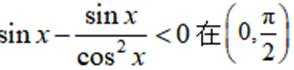
所以当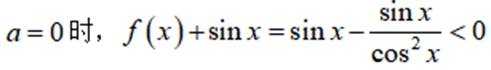
当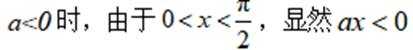
所以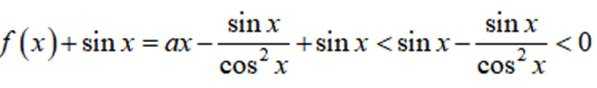
注意到
若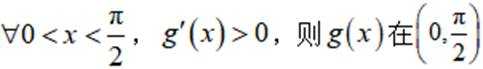
注意到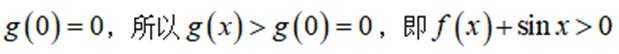
若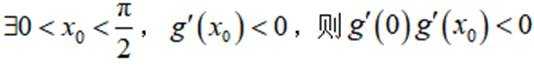
所以在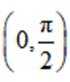
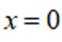

此时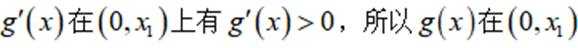
则在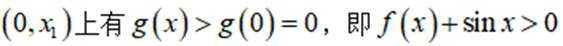
综上:
已知直线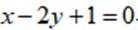
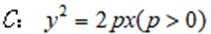
(1)求p;
(2)设F为C的焦点,M,N为C上两点,且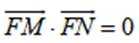
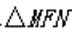
正确答案
(1)
(2)
解析
(1)利用直线与抛物线的位置关系,联立直线和抛物线方程求出弦长即可得出p;
(2)设直线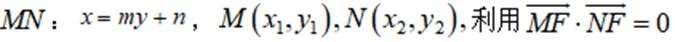
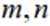
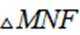
小问1详解
设
由
所以
即
小问2详解
因为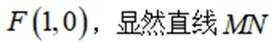
设直线
选做题
[选修4-4:坐标系与参数方程]
已知点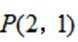
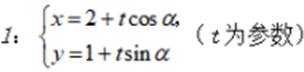
(1)求α;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求l的极坐标方程
[选修4-5:不等式选讲](10分)
设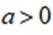
(1)求不等式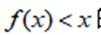
(2)若曲线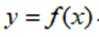
正确答案
(1)
(2)
解析
(1)根据t的几何意义即可解出;
(2)求出直线
小问1详解
因为
小问2详解
由(1)可知,直线
所以直线
由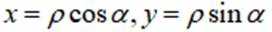

正确答案
(1)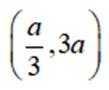
解析
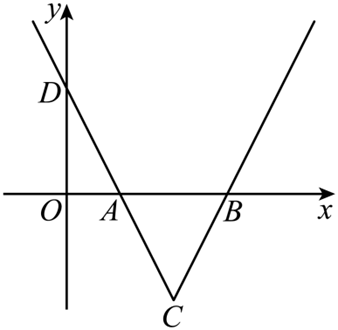
(1)分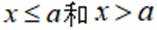
(2)写出分段函数,画出草图,表达面积解方程即可.
小问1详解
综上,不等式的解集为
小问2详解