- 真题试卷
- 模拟试卷
- 预测试卷
2.已知函数



正确答案
解析
由题可知:y=sin[w(x-




考查方向
本题主要考查三角函数的图像变换
解题思路
(1)求出变换后的函数解析式;(2)表示对称性,即可得到结果。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在表示图像变换时发生错误。
知识点
4.设曲线



正确答案
解析
由 题可知,g(x)=cosx,所以易得:A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查导数的几何意义
解题思路
(1)求出k;(2)判断图像,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求k时发生错误。
知识点
6.定义







正确答案
解析
由“均倒数”为

则
考查方向
本题主要考查数列的综合运算
解题思路
(1)求出an;(2)求出bn,利用裂项相消法求和,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求an时发生错误。
知识点
8.如图,网格纸是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为( )
正确答案
解析
由图可知,此多面体是一个以4为高,以长和宽分别是6、2的矩形为底的四棱锥。则V=sh/3=16。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查三视图
解题思路
(1)还原几何体;(2)求出体积,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在还原几何体时发生错误。
知识点
9.不等式



正确答案
解析
2x^2-axy+y^2>=0对任意x∈[1,2],y∈[1,3]恒成立, 等价于:a<=2x/y+y/x ① 对任意x∈[1,2],y∈[1,3]恒成立, 设t=x/y,x∈[1,2],y∈[1,3],则t∈[1/3,2], ①变为a<=2t+1/t,记为f(t), t=1/√2时f(t)取最小值

考查方向
本题主要考查不等式的应用
解题思路
(1)分离参数;(2)利用基本不等式求解,即可得到结果。
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在分离参数时发生错误。
知识点
10.过双曲线

正确答案
解析
由题可知,1<b/a<3, 则e2=1+b2/a2∈(2,10),则e∈
考查方向
本题主要考查直线与双曲线的位置关系
解题思路
(1)表示直线方程;(2)利用双曲线的几何性质表示离心率e,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在表示直线方程时发生错误。
知识点
1.若纯虚数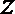
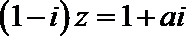
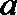
正确答案
解析
由题可知:(1-i)bi=b+bi=1+ai,则b=a=1。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
本题主要考查复数运算
解题思路
(1)设z=bi(b≠0);(2)表示两个复数相等,即可得到结果。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在表示复数相等时发生错误。
知识点
3.“

正确答案
解析
由题可知,当m>3时,方程我双曲线方程,反之不成立。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查双曲线和简易逻辑
解题思路
按照双曲线的标准方程求解B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断条件时发生错误。
知识点
5.如图,当输入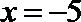
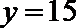
正确答案
解析
由题可知,当x=-5时,x=15+3=18,得x-y=18-15=3,x+y=18+15=33。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查程序
解题思路
(1)按照程序要求,依次计算y;(2)利用已知条件判断终止时的结果,即可得到结果。
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断条件时发生错误。
知识点
7.若关于

正确答案
解析
由图可知,当k=0或1时,刚好能构成等腰直角三角形,则面积为

考查方向
本题主要考查线性规划
解题思路
(1)表示平面区域;(2)求出区域面积,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在表示平面区域时发生错误。
知识点
11.已知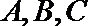
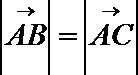
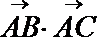
正确答案
解析
设: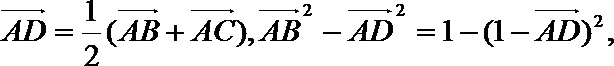
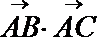
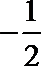
考查方向
本题主要考查平面向量
解题思路
(1)在单位圆中表示出向量;(2)利用圆的性质求解,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在化简时发生错误。
知识点
12.已知函数


正确答案
解析
令2x=t,(t>0)则当a=0时,y=t,符合题意;当a<0时,函数图像为“对勾函数”,只有a>=1才符合题意;同理,当a>0时,只有当a<=时符合题意。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查函数的性质的综合应用
解题思路
(1)对a分类讨论;(2)代入不同的a值,画出函数图像,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易利用指数函数图像时发生错误。
知识点
16.已知





正确答案
10
解析
考查方向
本题主要考查了解三角形和平面向量及不等式
解题思路
本题考查解三角形和平面向量及不等式,解题思路如下:(1)利用公式表示数量积;
(2)利用不等式求解。
易错点
本题必须注意数量积公式
知识点
13.已知函数



正确答案
7
解析
由题可知:k=f’(2)=1,f(2)=6,所以
考查方向
本题主要考查了导数的几何意义
解题思路
本题考查导数的几何意义,解题思路如下:利用导数的几何意义求出f’(2);利用切线方程求解。
易错点
本题必须注意导数的几何意义
知识点
14.已知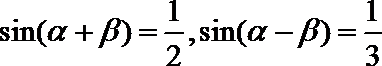

正确答案
1
解析
由题可知,将展开的两式相加减,可求出tana/tanb=5,代入对数式得值为1.
考查方向
本题主要考查了两角和差公式及对数运算
解题思路
本题考查两角和差公式及对数运算,解题思路如下:利用两角和差公式展开已知,两式相加减,求出正切值;代入对数式求解。
易错点
本题必须注意两角和差公式
知识点
15.为促进抚州市精神文明建设,评选省级文明城市,现省检查组决定在未来连续5天中随机选取2天对抚州的各项文明建设进行暗访,则这两天恰好为连续两天的概率 .
正确答案
解析
由题可知,P=4/10.
考查方向
本题主要考查了古典概型。
解题思路
本题考查古典概型,解题步骤如下:利用公式求解。
易错点
本题要注意概率计算。
知识点
17.在公比为




(Ⅰ)求
(Ⅱ)若函数








正确答案
见解析
解析
试题分析:本题属于数列和三角函数中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意图像的应用.
(Ⅰ) 解:由题可知

故
(Ⅱ)∵点

∴

如图,连接

又∵
∴
∴
∴
考查方向
本题考查了数列与三角函数的知识,涉及到等比数列及三角函数的应用,是高考题中的高频考点.
解题思路
本题考查数列与三角函数的知识,解题步骤如下:利用通项公式求解,利用函数图像性质代入求解。
易错点
三角函数图像易错。
知识点
18. 2015年9月3日,抗战胜利70周年纪念活动在北京隆重举行,受到全国人民的瞩目。纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这三个环节(可参加多个,也可都不参加)的情况及其概率如下表所示:
(Ⅰ)若
(Ⅱ)某医疗部门决定从(1)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
正确答案
见解析
解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
(Ⅰ)由题意可知:


故这60名抗战老兵中参加纪念活动的环节数为0,1,2,3的抗战老兵的人数分别为10,20,10,20,其中参加纪念活动的环节数为2的抗战老兵中应抽取的人数为
(Ⅱ)由(Ⅰ)可知抽取的这6名抗战老兵中1名参加了0个环节,记为



















记“这2名抗战老兵中至少有1人参加纪念活动的环节数为3”为事件










所以
考查方向
本题考查了概率统计问题.属于高考中的高频考点。
解题思路
本题考查概率统计,解题步骤如下:求出相应的概率;利用列举法求解。
易错点
概率表示。
知识点
19.如图,四棱柱








(Ⅰ)证明:平面

(Ⅱ)若


正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
试题解析:(Ⅰ)依题意


∵








(Ⅱ)取






∴四边形
可得



即异面直线


考查方向
本题考查了立体几何中的面面垂直和异面直线所成的角的问题.属于高考中的高频考点。
解题思路
本题考查立体几何,解题步骤如下:
(1)转化为证明线面垂直。
(2)找到三角形,利用余弦定理求解。
易错点
(1)第一问中的面面垂直的转化。(2)第二问中异面直线所成的角求解时要找到适当的三角形。
知识点
20.已知椭圆C:


(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知直线




正确答案
见解析
解析
试题分析:本题属于圆锥曲线中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意对参数的讨论.
试题解析:(Ⅰ)由题可知

所以椭圆的标准方程为
(Ⅱ)联立方程

则

设

即
又



综上可知,
考查方向
本题考查了直线与圆锥曲线的位置关系及综合应用,属于高考中的高频考点.
解题思路
本题考查圆锥曲线与直线的位置关系,解题步骤如下:
(1)利用e及对称性求a,b。
(2)联立直线与椭圆方程求解。
易错点
第二问中表示直线斜率时容易出错。
知识点
21.已知函数




(Ⅰ)当


(Ⅱ)若


正确答案
见解析
解析
本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)要注意对参数的讨论.
(Ⅰ)由










(Ⅱ)由







由



因此,当





所以


设








所以
因此,对任意

考查方向
本题考查了利用导数的几何意义和综合应用,分类讨论,讨论点大体可以分成以下几类:
(1)根据判别式讨论;
(2)根据二次函数的根的大小;
(3)定义域由限制时,根据定义域的隐含条件;
(4)求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
(5)多次求导求解等.
解题思路
本题考查导数的几何意义和综合应用,解题步骤如下:
(1)求导,然后求切线方程。
(2)对参数分类讨论证得结论。
易错点
第二问中的易丢对x的分类讨论。
知识点
22.选修4-1:几何证明选讲
如图,












(Ⅰ)求证:

(Ⅱ)若

正确答案
见解析
解析
试题分析:本题属于平面几何中的基本问题,题目的难度是容易题。
(Ⅰ)连接

又




(Ⅱ)过




设

由


可得
考查方向
本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
解题思路
本题考查平面几何的知识,解题步骤如下:
(1)利用圆的相关定理证明。
(2)利用切割线定理和相交弦定理证明。
易错点
相关的定理容易混用。