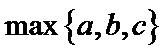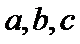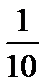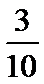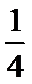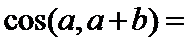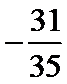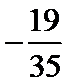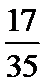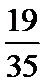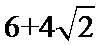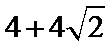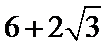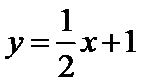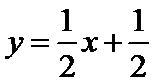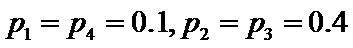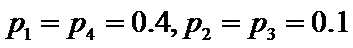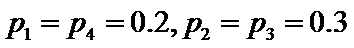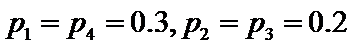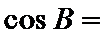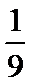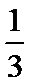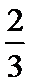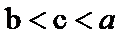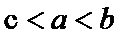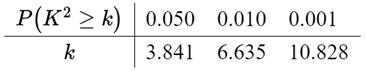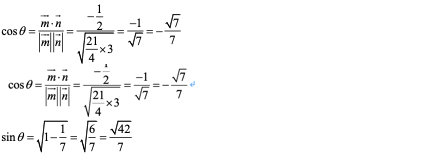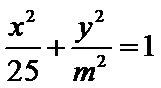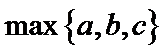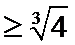- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合A=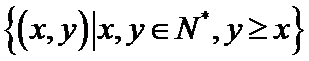
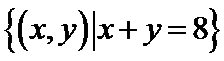
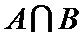
正确答案
2.复数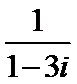
正确答案
4. Logistic模型是常用数学模型之一,可应用于流行病学领域,有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数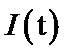
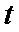
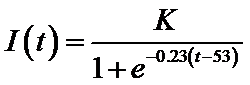
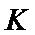
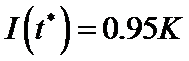
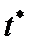
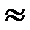
正确答案
5. 设O为坐标原点,直线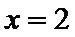
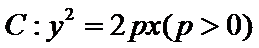
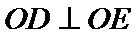
正确答案
6. 已知向量a,b满足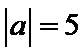
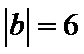
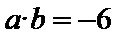
正确答案
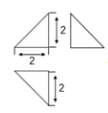
8. 右图为某几何体的三视图,则该几何体的表面积是
正确答案
9.已知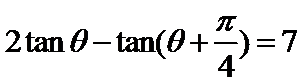
正确答案
10.若直线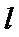
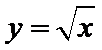
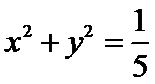
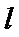
正确答案
3.在一组样本数据中,1,2,3,4出现的频率分别为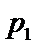
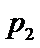
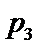
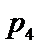
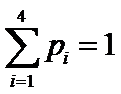
正确答案
7. 在△ABC中,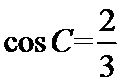
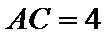
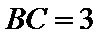
正确答案
11. 设双曲线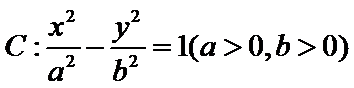
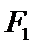
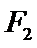
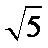
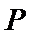
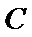
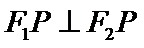
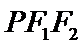
正确答案
12. 已知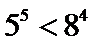
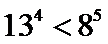
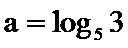
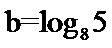
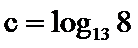
正确答案
13. 若x,y满足约束条件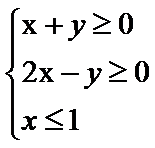
正确答案
7
14. 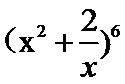
正确答案
240
15.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为____.
正确答案
16.关于函数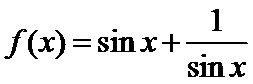
①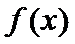
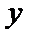
②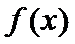
③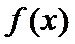
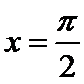
④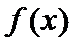
其中所有真命题的序号是____.
正确答案
②③
18. (12分)
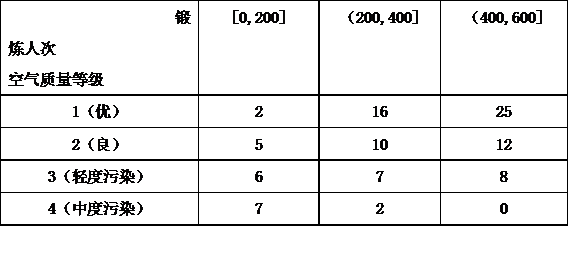
某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
(1) 分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2) 求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
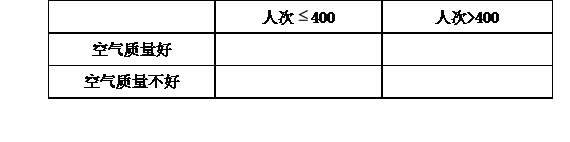
(3) 若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”。根据所给数据,完成下面的
附:, 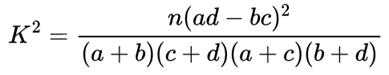
正确答案
19. (12分)
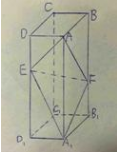
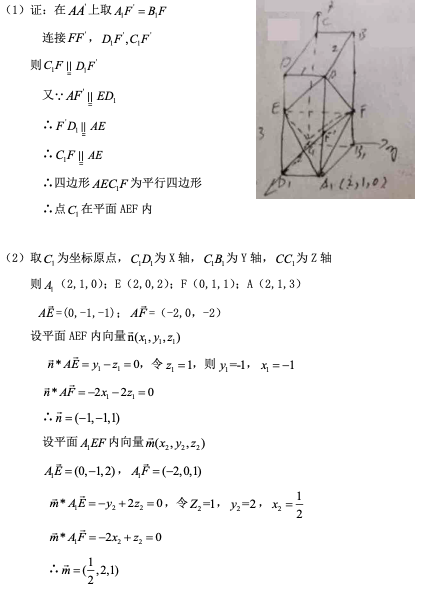
如图,在长方体
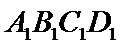
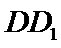
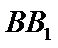
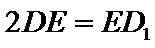
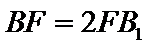
(1)证明:点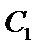
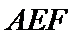
(2)若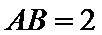
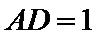
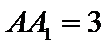
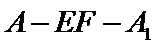
正确答案
20. (12分)
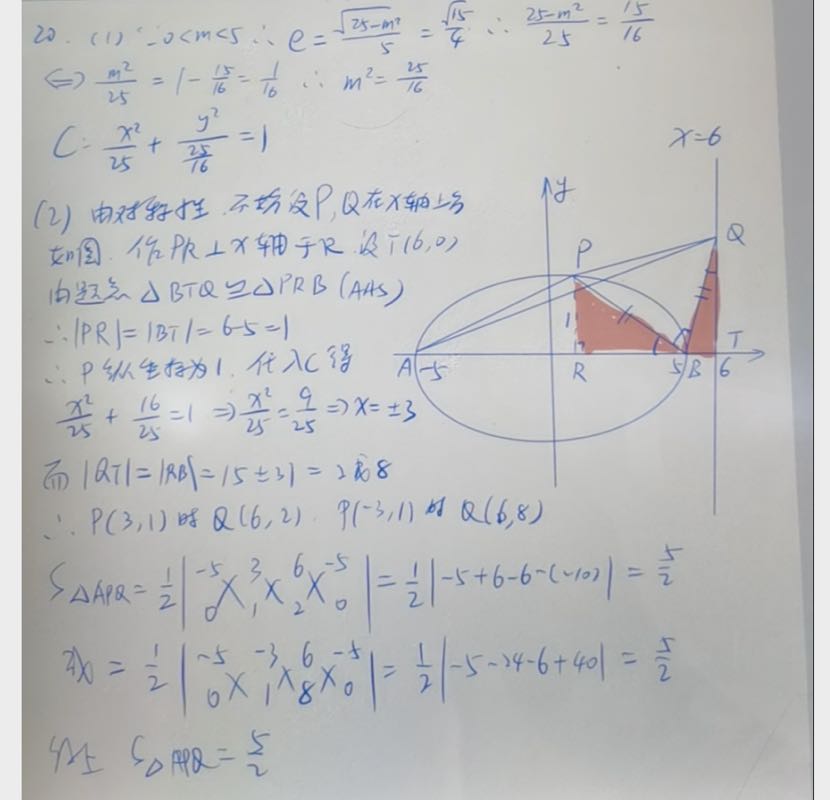
已知椭圆C:
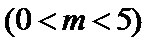
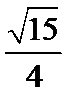
(1)求C的方程;
(2)若点P在C上,点Q在直线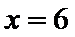
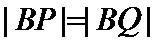
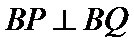
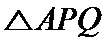
正确答案
17. (12分)
设数列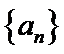
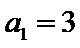
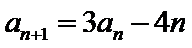
(1)计算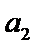
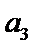
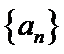
(2)求数列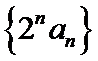
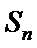
正确答案
21. (12分)
设函数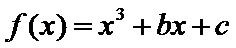
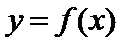
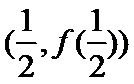
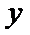
(1)求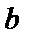
(2)若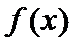
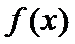
正确答案
(二)选考题:共10分,请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
(1)22. [选修4—4:坐标系与参数方程] (10分)
在直角坐标系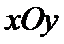
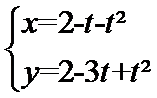
(1)求|AB|;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求直线AB的极坐标方程.
(2)23. [选修4—5:不等式选讲](10分)
设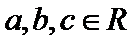
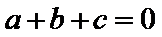
(1) 证明: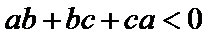
(2) 用