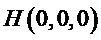- 真题试卷
- 模拟试卷
- 预测试卷
2.已知集合


正确答案
解析
试题分析:集合


考查方向
解题思路
集合的交、并、补运算问题,应先把集合化简在计算,常常借助数轴或韦恩图处理.
易错点
忽略
知识点
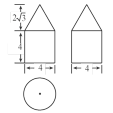
6.下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
正确答案
解析
试题分析:由题意可知,圆柱的侧面积为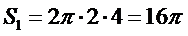
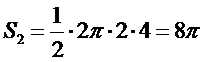
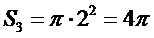
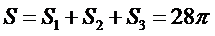
考查方向
解题思路
由三视图可知该几何体的直观图,然后即可求出多面体的体积。
易错点
不能将三视图还原为原图导致出错。
知识点
8.中国古代有计算多项式值的秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的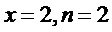


正确答案
解析
C
第一次运算: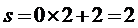
第二次运算: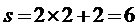
第三次运算: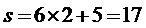
故选C.
考查方向
解题思路
求解此类问题一般是把人看作计算机,按照程序逐步列出运行结果。
易错点
不知何时终止循环导致出错。
知识点
1.已知

正确答案
解析
A
∴


考查方向
解题思路
复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可。
易错点
对复数的几何意义不熟悉导致出错。
知识点
3.已知向量


正确答案
解析
试题分析:向量



考查方向
解题思路
直接根据向量的坐标运算公式及向量垂直的坐标表示进行计算。
易错点
不熟悉向量的坐标运算公式导致出错。
知识点
4.圆

正确答案
解析
A
圆

故圆心为


故选A.
考查方向
解题思路
化圆的方程为标准方程,再根据点到直线的距离公式进行计算。
易错点
不能熟记点到直线的距离公式导致出错。
知识点
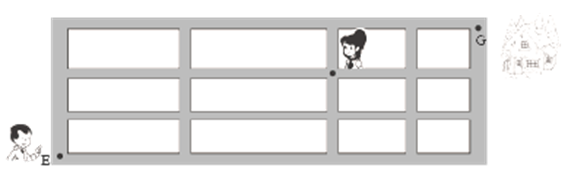
5.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
正确答案
解析
B
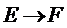
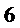
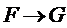
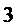
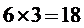
故选B.
考查方向
解题思路
从实际问题中抽出数学模型,再根据两个原理进行计算。
易错点
不能从实际问题中抽出数学模型导致出错。
知识点
7.若将函数

正确答案
解析
B
平移后图像表达式为
令

故选B.
考查方向
解题思路
先根据平移变换公式求出平移后的表达式,再根据对称性求出对称轴方程.
易错点
忽略平移变换和伸缩变换都是针对x而言,即x本身加减多少值,而不是依赖于ωx加减多少值导致出错.
知识点
9.若

正确答案
解析
试题分析:
且
考查方向
解题思路
直接根据三角恒等变换公式进行计算。
易错点
对三角恒等变换公式不熟悉导致出错。
知识点
10.从区间












正确答案
解析
试题分析:利用几何概型,圆形的面积和正方形的面积比为

考查方向
解题思路
先确定几何度量,再根据几何概型的概率计算公式即可求解。
易错点
不能准确选择几何度量导致出错。
知识点
12.已知函数





正确答案
解析
B
由


而

∴对于每一组对称点

∴
考查方向
解题思路
根据已知条件判断出函数的对称中心,再利用对称性即可求出
易错点
不能由
知识点
11.已知


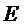
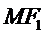
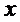
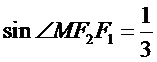
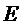
正确答案
解析
A
离心率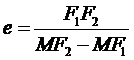

故选A.
考查方向
解题思路
根据双曲线的定义及正弦定理直接计算即可。
易错点
不能准确区分双曲线中a,b,c的关系与椭圆中a,b,c的关系导致出错。
知识点
15.有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 .
正确答案
1和3
解析
试题分析:由题意分析可知甲的卡片上数字为1和3,乙的卡片上数字为2和3,丙卡片上数字为1和2.
考查方向
解题思路
从题中所给信息出发,逐步推导,即可得出结论。
易错点
不能保持思维的严密性、一贯性导致出错。
知识点
16.若直线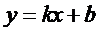
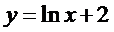
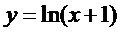
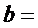
正确答案
解析
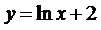
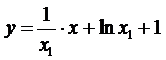
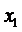
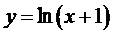
∴
解得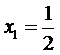
∴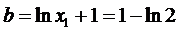
考查方向
解题思路
根据导数的几何意义进行计算即可求出b的值。
易错点
不能分清在点P处的切线与过P点的切线的不同导致出错。
知识点
13.
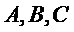





正确答案
解析
试题分析:因为




所以
考查方向
解题思路
先根据


易错点
相关知识点不熟悉导致出错。
教师点评
三角函数和差公式,正弦定理.
知识点
14. 

(1)如果

(2)如果

(3)如果

(4)如果




其中正确的命题有 . (填写所有正确命题的编号)
正确答案
②③④
解析
试题分析:对于①,







考查方向
解题思路
根据相关定理直接进行判断。
易错点
忽略在空间中考虑线、面关系导致出错。
知识点








17.求
18.求数列
正确答案
(Ⅰ)


解析
试题分析:本题属于数列与函数的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
试题解析:(Ⅰ)设


所以
考查方向
解题思路
(Ⅰ)先用等差数列的求和公式求公差




易错点
对取整函数的性质不熟悉导致出错。
正确答案
(Ⅱ)1893.
解析
试题分析:本题属于数列与函数的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
⑵记



当

当

当

当

∴
考查方向
解题思路
(Ⅱ)对


易错点
对取整函数的性质不熟悉导致出错。
已知椭圆









24.当

25.当

正确答案
(Ⅰ)
解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
(I)设





由已知及椭圆的对称性知,直线



将





因此

因此


考查方向
解题思路
(1)先求出直线AM的方程,再求点M的纵坐标,最后求
易错点
不知如何运用题中所给条件导致本题没思路。
正确答案
(Ⅱ)
解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
⑵直线AM的方程为
联立
解得

所以
所以
因为
所以

因为椭圆E的焦点在x轴,所以

解得


考查方向
解题思路
(2)设



易错点
不知如何运用题中所给条件导致本题没思路。
某险种的基本保费为
设该险种一续保人一年内出险次数与相应概率如下:
19.求一续保人本年度的保费高于基本保费的概率;
20.若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
21.求续保人本年度的平均保费与基本保费的比值.
正确答案
(Ⅰ)0.55;
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
试题解析:(Ⅰ)设

考查方向
解题思路
(Ⅰ)根据互斥事件的概率公式求一续保人本年度的保费高于基本保费的概率;
易错点
相关知识点不熟容易出错。
正确答案
(Ⅱ)
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
(Ⅱ)设


又
因此所求概率为
考查方向
解题思路
(Ⅱ)一续保人本年度的保费高于基本保费,当且仅当一年内出险次数大于3,由条件概率公式求解;
易错点
相关知识点不熟容易出错。
正确答案
(Ⅲ)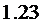
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
⑶解:设本年度所交保费为随机变量
平均保费

∴平均保费与基本保费比值为
考查方向
解题思路
(Ⅲ)记续保人本年度的保费为

易错点
相关知识点不熟容易出错。
如图,菱形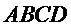
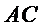
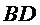
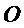
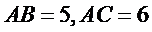
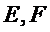
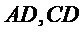
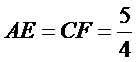
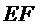
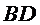
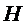
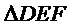
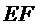
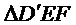
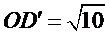
22.证明: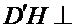
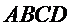
23.求二面角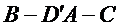

正确答案
(Ⅰ)详见解析;
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
⑴证明:∵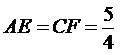
∴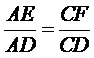
∴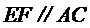
∵四边形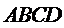
∴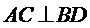
∴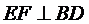
∴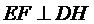
∴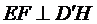
∵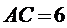
∴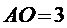
又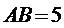
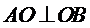
∴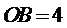
∴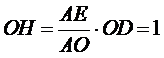
∴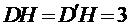
∴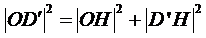
∴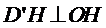
又∵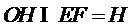
∴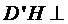
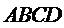
考查方向
解题思路
(1)先证明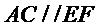
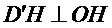
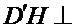
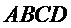
易错点
解题步骤不完整或考虑不全致推理片面导致出错。
正确答案
(Ⅱ)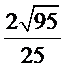
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
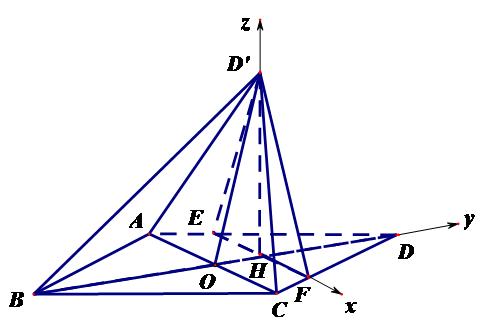
(II)如图,以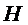
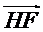
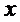
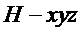
则
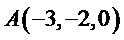
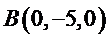
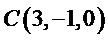
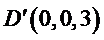
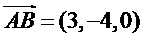
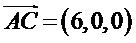
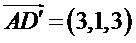
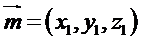
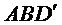
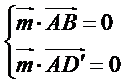
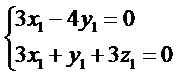
所以可以取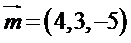
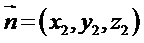
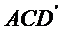
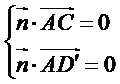
即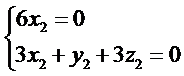
所以可以取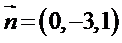
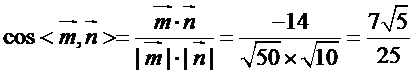
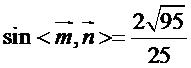
因此二面角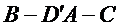
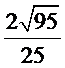
考查方向
解题思路
(2)建立空间直角坐标系,分别求出两个平面的法向量,再利用公式即可求出二面角.
易错点
解题步骤不完整或考虑不全致推理片面导致出错。
回答下列各题
26.讨论函数


27.证明:当




正确答案
(Ⅰ)详见解析;
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
⑴证明:
∵当
∴

∴
∴
考查方向
解题思路
(1)先求定义域,用导数法求函数的单调性,当

易错点
第二问对题中所给条件不知如何下手导致失分。
正确答案
(Ⅱ)
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
⑵
由(1)知,当


使得
当





记



∴
考查方向
解题思路
(2)用导数法球函数

易错点
第二问对题中所给条件不知如何下手导致失分。
请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号
选修4-1:几何证明选讲(请回答28、29题)
如图,在正方形






选修4—4:坐标系与参数方程(请回答30、31题)
在直角坐标系


选修4—5:不等式选讲(请回答32、33题)
已知函数


28.证明:
29.若



30.以坐标原点为极点,

31.直线







32.求
33.证明:当

正确答案
(Ⅰ)详见解析;
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
(Ⅰ)证明:∵
∴
∴
∵
∴
∴
∴
∴
∴
∴B,C,G,F四点共圆.
考查方向
解题思路
(1)利用三角形相似即可证明四点共圆;
易错点
对相关定理不熟悉导致本题失分。
正确答案
(Ⅱ)
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
(II)由



由



因此四边形



考查方向
解题思路
(2)由四点共圆可得





易错点
对相关定理不熟悉导致本题失分。
正确答案
(Ⅰ)
解析
试题分析:本题属于坐标系与参数方程的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
试题解析:(I)由

考查方向
解题思路
(1)直接利用互化公式即可求出极坐标方程;
易错点
不能熟记极坐标方程与参数方程的互化公式及应用导致本题出错。
正确答案
(Ⅱ)
解析
试题分析:本题属于坐标系与参数方程的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(II)在(I)中建立的极坐标系中,直线
由



于是
由

所以


考查方向
解题思路
(2)先求出直线l的极坐标方程,将其带入C的极坐标方程得到关于

易错点
不能熟记极坐标方程与参数方程的互化公式及应用导致本题出错。
正确答案
(Ⅰ)
解析
试题分析:本题属于不等式的选讲内容,不等式证明选讲多以绝对值不等式为载体命制试题,主要涉及图像、解不等式、由不等式恒成立求参数范围等,解决此类问题通常转换为分段函数求解,注意不等式的解集一定要写出集合形式,属于简单题,只要掌握相关不等式的知识,即可解决本题,解析如下:
(I)
当



当

当



所以

考查方向
解题思路
(1)根据零点分段讨论法直接求解;
易错点
第二问不知如何运用已知条件导致此问无思路。
正确答案
(Ⅱ)详见解析.
解析
试题分析:本题属于不等式的选讲内容,不等式证明选讲多以绝对值不等式为载体命制试题,主要涉及图像、解不等式、由不等式恒成立求参数范围等,解决此类问题通常转换为分段函数求解,注意不等式的解集一定要写出集合形式,属于简单题,只要掌握相关不等式的知识,即可解决本题,解析如下:
(II)由(I)知,当

从而
因此
考查方向
解题思路
(2)采用平方作差法,再临行因式分解,进而可证当

易错点
第二问不知如何运用已知条件导致此问无思路。