- 真题试卷
- 模拟试卷
- 预测试卷
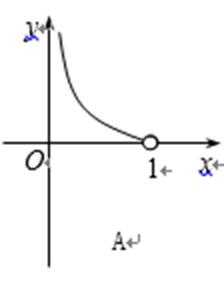
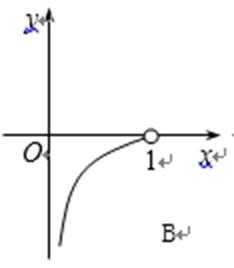
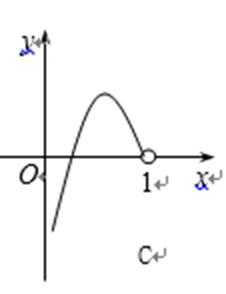
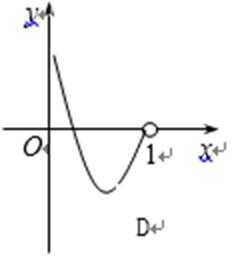
5.函数




正确答案
解析
略。
知识点
4.某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
正确答案
解析
略。
知识点
6.在递增的等比数列


正确答案
解析
略。
知识点
7.某校为了解本校高三学生学习心里状态,采用系统抽样方法从800人中抽取40人参加某种测试,为此将题目随机编号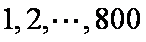
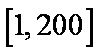
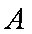
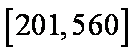


正确答案
解析
略。
知识点
2.某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则其侧视图的面积是( )
正确答案
解析
略。
知识点
3.设随机变量X服从正态分布

正确答案
解析
略。
知识点
1.已知集合

正确答案
解析
略。
知识点
8.已知函数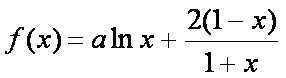
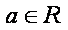

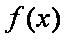
正确答案
解析
略。
知识点
10.若从区间

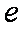
正确答案
解析
略。
知识点
9.不等式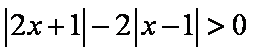
正确答案
1
解析
略。
知识点
15.如图,⊙










正确答案
解析
略。
知识点
14.直线l的参数方程是

正确答案
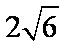
解析
略。
知识点
12.若幂函数

正确答案
解析
略。
知识点
11.设等差数列





正确答案
121
解析
设数列


即

知识点
13.从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有________。
正确答案
240种。
解析
根据题意,由排列可得,从6名志愿者中选出4人分别从事四项不同工作,有A=360种不同的情况,其中包含甲从事翻译工作,有A=60种,乙从事翻译工作,有A=60种,若其中甲、乙两名志愿者都不能从事翻译工作,则选派方案共有360-60-60=240种。
知识点
18.如图1,在直角梯形









(1)求证:
(2) 求

(3)判断直线

正确答案
见解析。
解析
(1)
证明:因为 四边形
所以 
因为 平面





所以 

因为 

所以 
(2)如图,以点



设

所以 


设平面

由
令


设


则
所以 


(3)
直线

由题意得,
所以 
所以 
因为 

所以 
另解:直线

取






所以 

因为 


所以 

所以 

所以 
所以 

因为 四边形

所以 


所以 



所以 


知识点
16.已知在




(1)求角
(2)若

正确答案
见解析。
解析
(1)由

于是

(2)∵


由正弦定理可知,
又
∴
知识点
19.已知正项数列{




(1)求数列{
(2)令


正确答案
见解析。
解析
(1)当

当
两式相减得 
所以数列

(2)
在

知识点
17.某超市从2015年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个, 并按
假设甲、乙两种酸奶独立销售且日销售量相互独立
(1)写出频率分布直方图(甲)中


(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(3)设

正确答案
见解析。
解析
(1)

(2)设事件
事件
事件
不高于20箱. 则

所以 
(3)由题意可知,




所以
所以 

另解:由题意可知
所以 

知识点
20.已知椭圆



(1) 求椭圆
(2)已知过椭圆













正确答案
见解析。
解析
(1)





(2)点

















当且仅当




知识点
21.设函数



(1)求
(2)当



(3)求证:
正确答案
见解析。
解析
(1) 对

根据条件知

(2)由(Ⅰ)得

①当


于是






②当


于是






③当


当








④当


当








综上可知,所求实数

(3)对要证明的不等式等价变形如下:
所以可以考虑证明:对于任意的正整数


对于








当

从而对于任意正整数

对于







因此对于任意正整数

这样依据不等式


即可得到