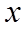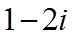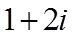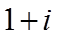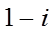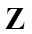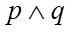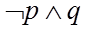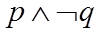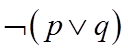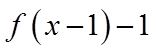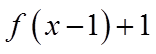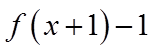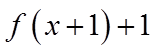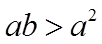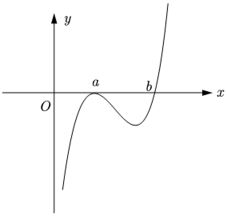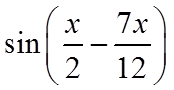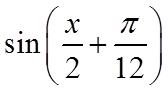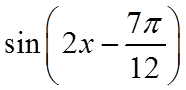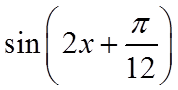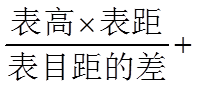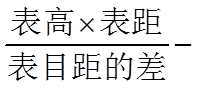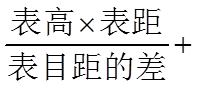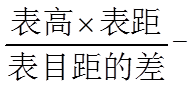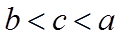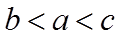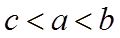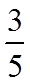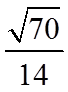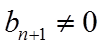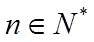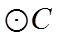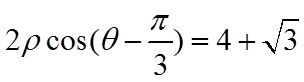- 真题试卷
- 模拟试卷
- 预测试卷
1. 设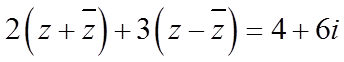

正确答案
解析
设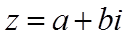
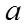
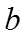
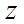
【详解】设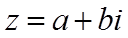
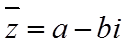
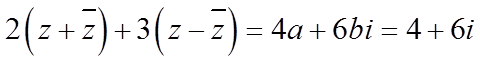
所以,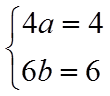
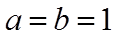
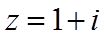
故选:C.
2. 已知集合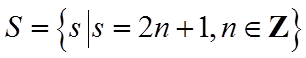
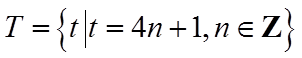
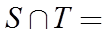
正确答案
解析
分析可得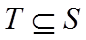
【详解】任取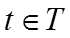
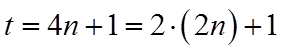
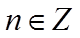

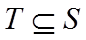
因此,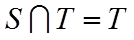
故选:C.
3. 已知命题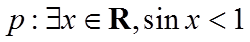
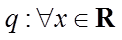
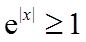
正确答案
解析
由正弦函数的有界性确定命题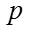
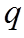
【详解】由于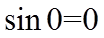
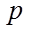
由于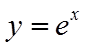
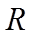
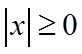
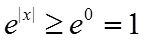
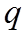
所以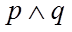
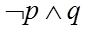
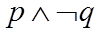
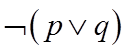
故选:A.
4. 设函数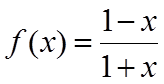
正确答案
解析
分别求出选项的函数解析式,再利用奇函数的定义即可.
【详解】由题意可得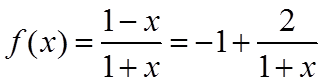
对于A,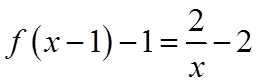
对于B,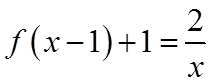
对于C,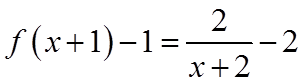
对于D,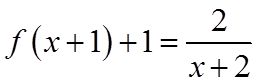
故选:B
【点睛】本题主要考查奇函数定义,考查学生对概念
6. 将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( )
正确答案
解析
先确定有一个项目中分配2名志愿者,其余各项目中分配1名志愿者,然后利用组合,排列,乘法原理求得.
【详解】根据题意,有一个项目中分配2名志愿者,其余各项目中分配1名志愿者,可以先从5名志愿者中任选2人,组成一个小组,有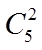
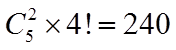
故选:C.
【点睛】本题考查排列组合的应用问题,属基础题,关键是首先确定人数的分配情况,然后利用先选后排思想求解.
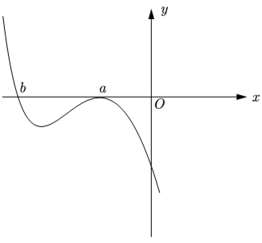
10. 设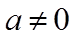
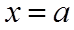
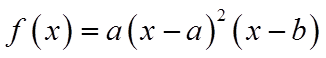
正确答案
解析
先考虑函数的零点情况,注意零点左右附近函数值是否编号,结合极大值点的性质,对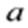
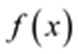
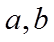
【详解】若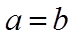
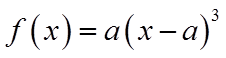
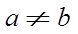
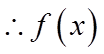
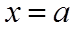
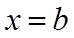
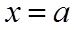
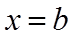
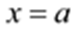
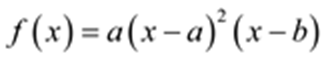
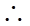
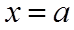
当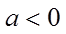
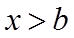

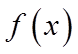
由图可知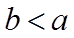
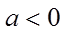
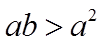
当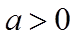
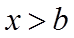
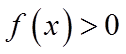
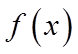
由图可知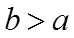
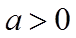
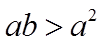
综上所述,
故选:D
【点睛】本小题主要考查三次函数的图象与性质,利用数形结合的数学思想方法可以快速解答.
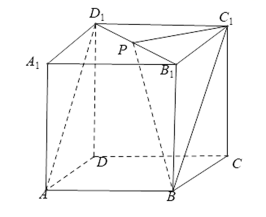
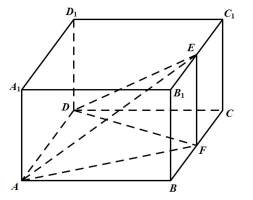
5. 在正方体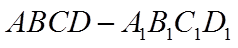
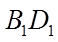
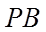
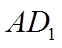
正确答案
解析
平移直线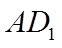
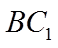
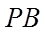
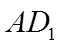
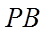
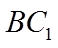
【详解】
如图,连接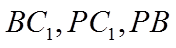
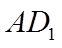
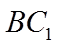
所以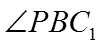
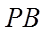
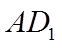
因为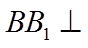
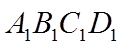
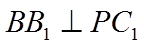
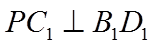
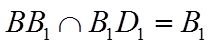
所以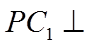
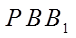
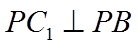
设正方体棱长为2,则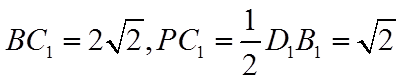
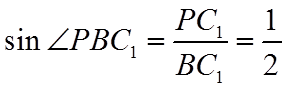
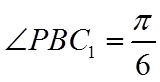
故选:D
7. 把函数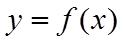

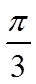
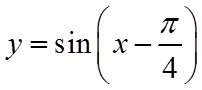
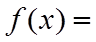
正确答案
解析
解法一:从函数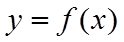
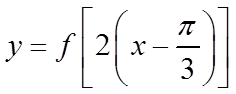
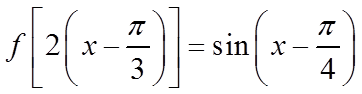
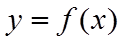
解法二:从函数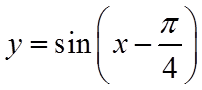
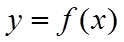
【详解】解法一:函数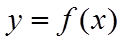
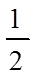
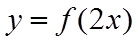
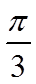
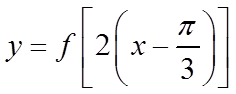
根据已知得到了函数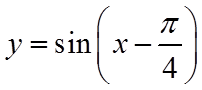
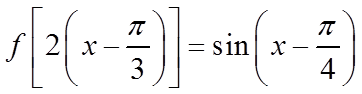
令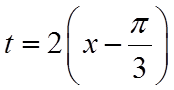
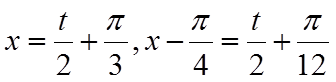
所以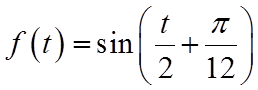
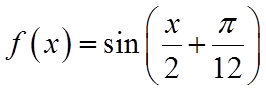
解法二:由已知的函数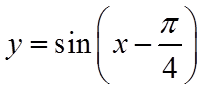
第一步:向左平移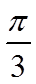
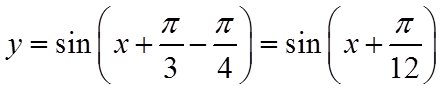
第二步:图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,得到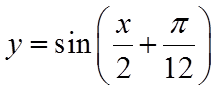
即为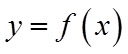
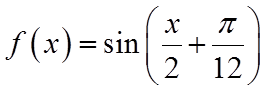
故选:B.
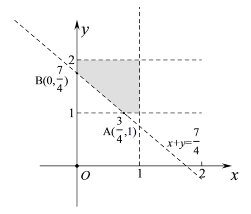
8. 在区间

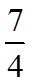
正确答案
解析
设从区间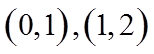
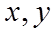
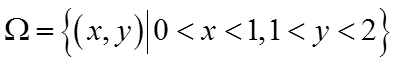
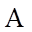
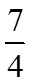
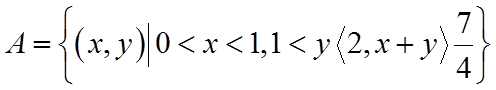
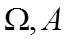
【详解】如图所示:
设从区间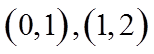
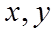
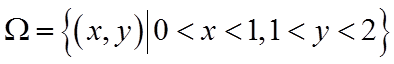
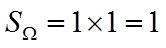
设事件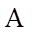
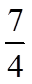
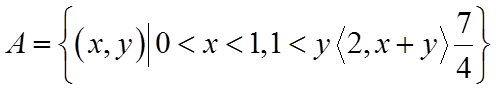
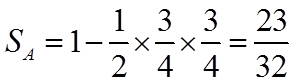
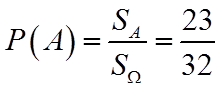
故选:B.
【点睛】本题主要考查利用线性规划解决几何概型中的面积问题,解题关键是准确求出事件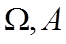
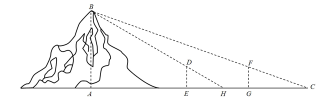
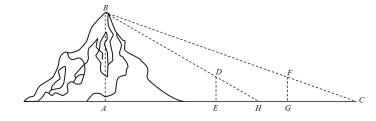
9. 魏晋时刘徽撰写的《海岛算经》是关测量的数学著作,其中第一题是测海岛的高.如图,点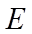
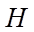
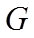
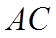
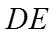
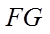
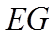
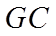
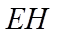
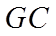
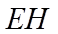
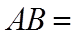
正确答案
解析
利用平面相似的有关知识以及合分比性质即可解出.
【详解】如图所示:
由平面相似可知,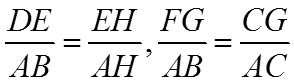
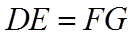
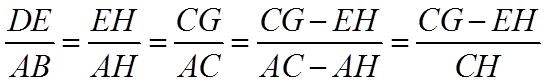
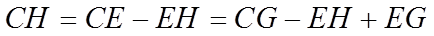
即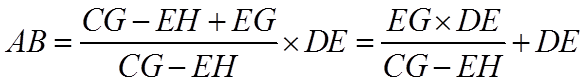

故选:A.
【点睛】本题解题关键是通过相似建立比例式,围绕所求目标进行转化即可解出.
11. 设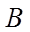
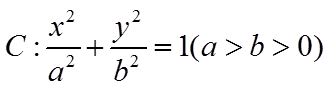
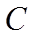
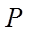
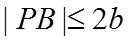
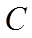
正确答案
解析
设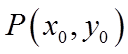
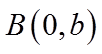
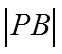
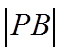
【详解】设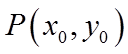
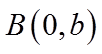
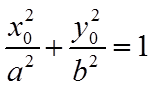
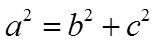
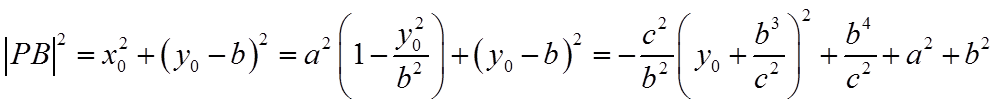
因为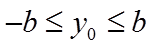
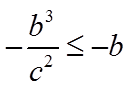
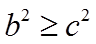
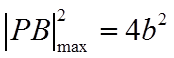
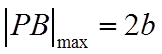
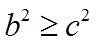
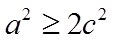
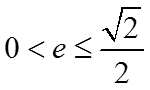
当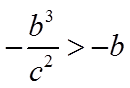
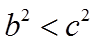
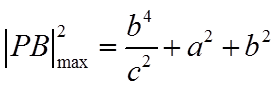
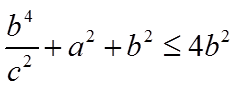
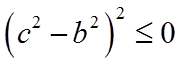
故选:C.
【点睛】本题解题关键是如何求出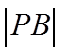
12. 设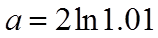
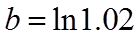
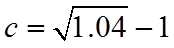
正确答案
解析
利用对数的运算和对数函数的单调性不难对a,b的大小作出判定,对于a与c,b与c的大小关系,将0.01换成x,分别构造函数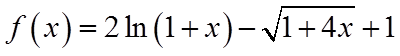
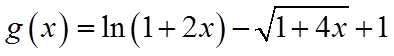

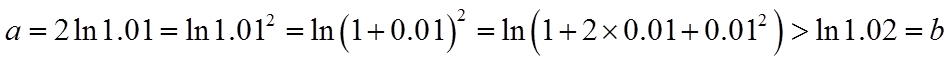
所以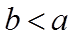
下面比较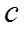
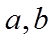
记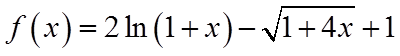
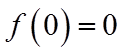
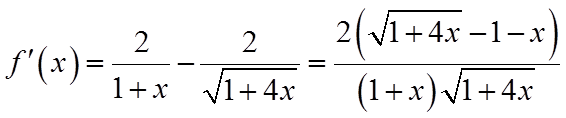
由于
所以当0<x<2时,
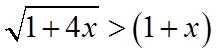
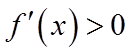
所以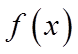
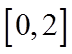
所以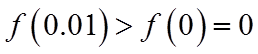
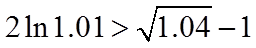
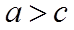
令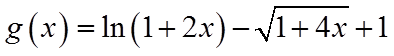
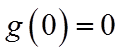
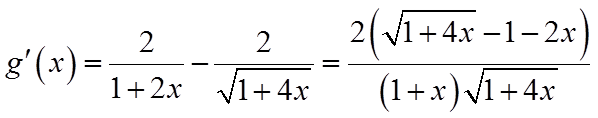
由于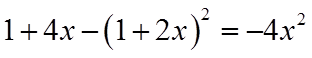
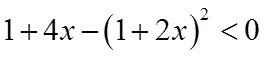
所以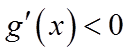
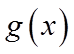
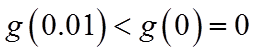
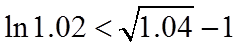
综上,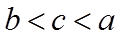
故选:B.
【点睛】本题考查比较大小问题,难度较大,关键难点是将各个值中的共同的量用变量替换,构造函数,利用导数研究相应函数的单调性,进而比较大小,这样的问题,凭借近似估计计算往往是无法解决的.
13. 已知双曲线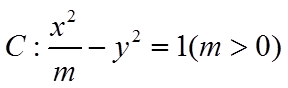
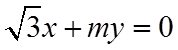
正确答案
4
解析
将渐近线方程化成斜截式,得出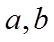
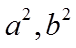
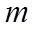
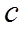
【详解】由渐近线方程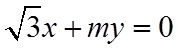
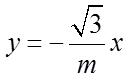
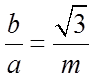
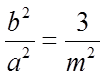
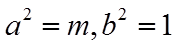
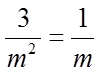
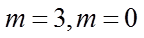
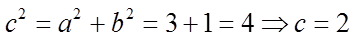
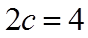
故答案为:4.
【点睛】本题为基础题,考查由渐近线求解双曲线中参数,焦距,正确计算并联立关系式求解是关键.
15. 记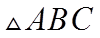
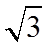
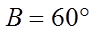
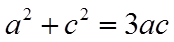
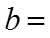
正确答案
解析
由三角形面积公式可得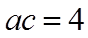
【详解】由题意,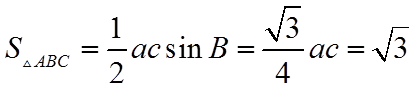
所以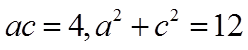
所以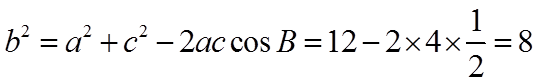
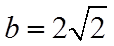
故答案为: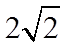
14. 已知向量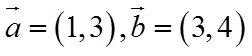
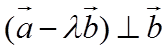
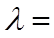
正确答案
解析
根据平面向量数量积的坐标表示以及向量的线性运算列出方程,即可解出.
【详解】因为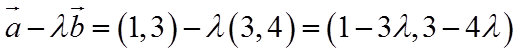
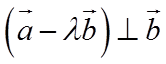
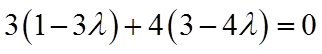
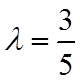
故答案为: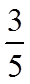
【点睛】本题解题关键是熟记平面向量数量积的坐标表示,设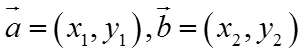
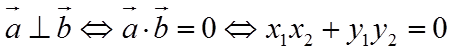
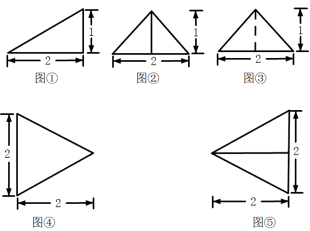
16. 以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________(写出符合要求的一组答案即可).
正确答案
③④(答案不唯一)
解析
由题意结合所给的图形确定一组三视图的组合即可.
【详解】选择侧视图为③,俯视图为④,
如图所示,长方体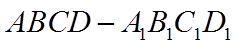
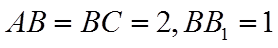
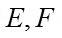
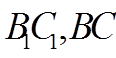
则正视图①,侧视图③,俯视图④对应的几何体为三棱锥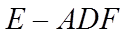
故答案为:③④.
【点睛】三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系.
17. 某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备和新设备生产产品的该项指标的样本平均数分别记为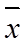
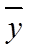
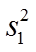
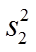
(1)求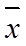
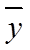
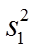
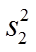
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果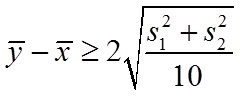
正确答案
(1)
解析
(1)根据平均数和方差的计算方法,计算出平均数和方差.
(2)根据题目所给判断依据,结合(1)的结论进行判断.
【详解】(1)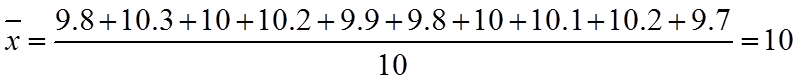
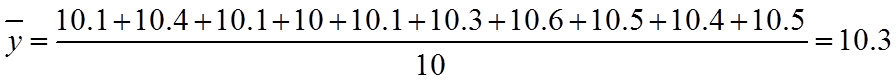
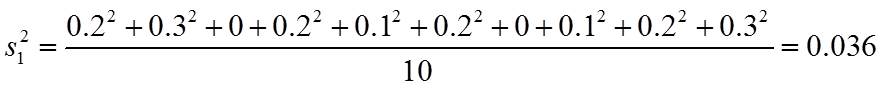
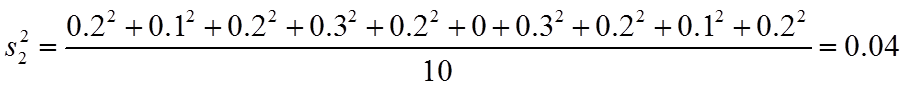
(2)依题意,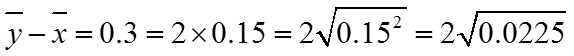
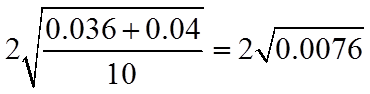
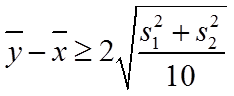
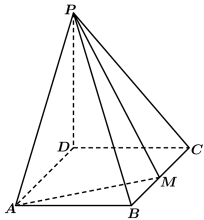
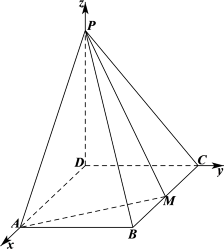
18. 如图,四棱锥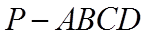
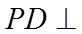
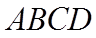
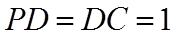
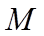
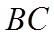
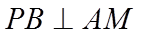
(1)求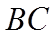
(2)求二面角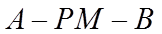
正确答案
(1)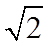
解析
(1)以点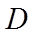
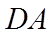
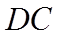
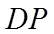
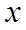
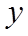
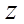
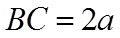
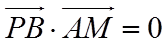
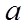
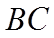
(2)求出平面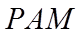
【详解】(1)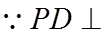
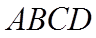
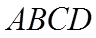
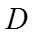
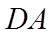
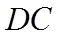
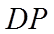
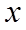
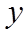
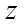
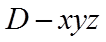
设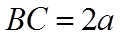
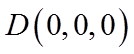
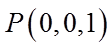
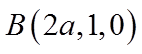
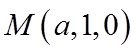

则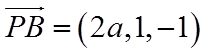

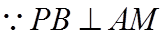
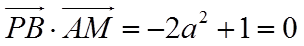
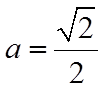
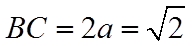
(2)设平面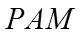
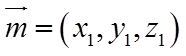
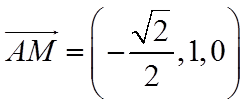
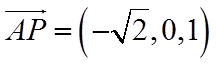
由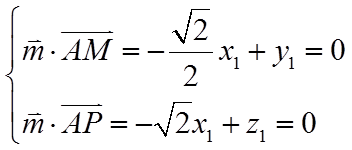
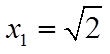
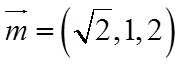
设平面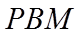
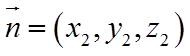
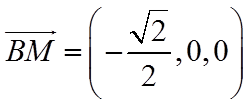
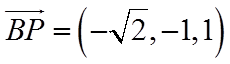
由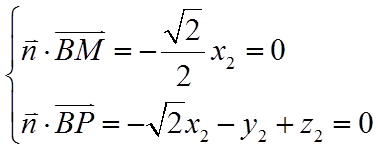
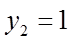
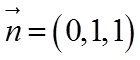
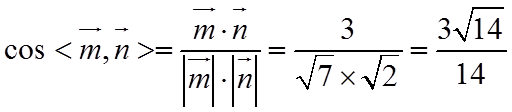
所以,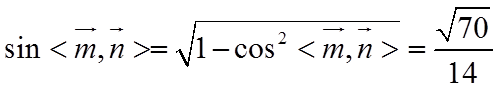
因此,二面角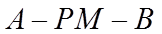
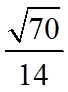
【点睛】思路点睛:利用空间向量法求解二面角的步骤如下:
(1)建立合适的空间直角坐标系,写出二面角对应的两个半平面中对应的点的坐标;
(2)设出法向量,根据法向量垂直于平面内两条直线的方向向量,求解出平面的法向量(注:若半平面为坐标平面,直接取法向量即可);
(3)计算(2)中两个法向量的余弦值,结合立体图形中二面角的实际情况,判断二面角是锐角还是钝角,从而得到二面角的余弦值.
19. 记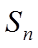
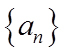
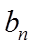
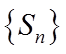
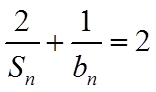
(1)证明:数列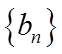
(2)求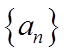
正确答案
(1)证明见解析;(2)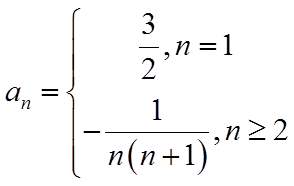
解析
(1)由已知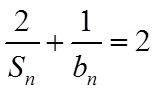
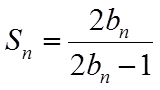
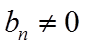
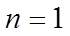
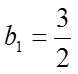
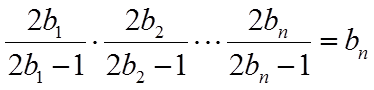
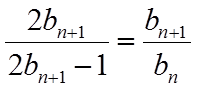
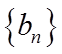
(2)由(1)可得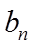
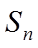
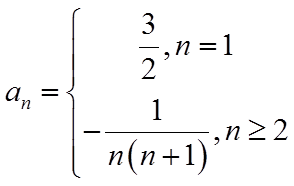
【详解】(1)由已知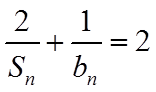
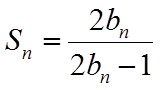
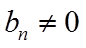
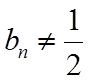
取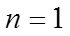
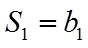
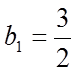
由于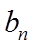
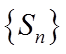
所以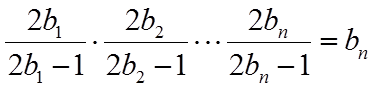
所以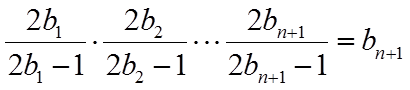
所以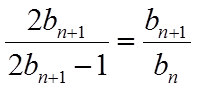
由于
所以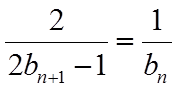
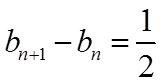
所以数列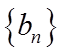
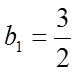
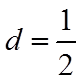
(2)由(1)可得,数列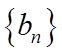
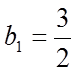
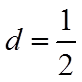
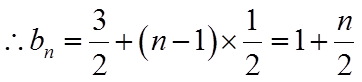
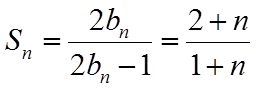
当n=1时,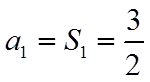
当n≥2时,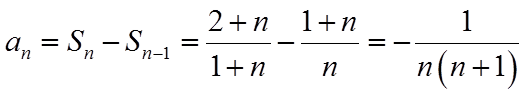
∴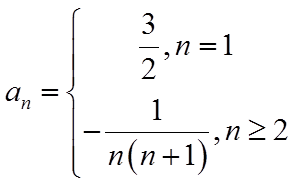
【点睛】本题考查等差数列的证明,考查数列的前n项和与项的关系,数列的前n项积与项的关系,其中由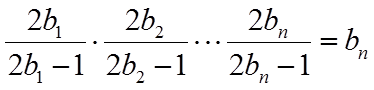
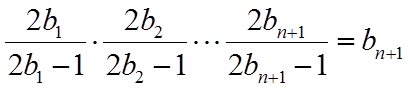
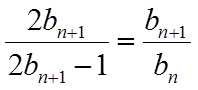
20. 设函数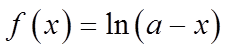
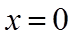
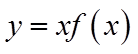
(1)求a;
(2)设函数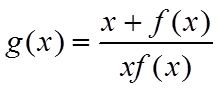
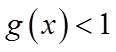
正确答案
(1)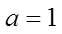
解析
(1)由题意求出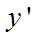
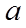
(2)由(1)得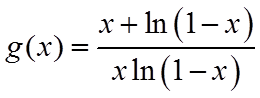
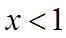
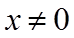
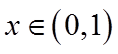
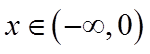
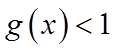
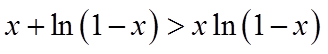
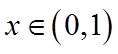
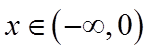
【详解】(1)由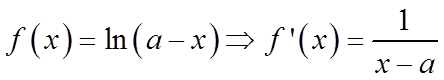
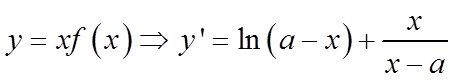
又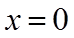
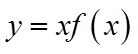
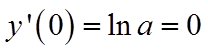
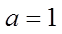
(2)由(1)得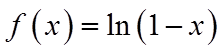
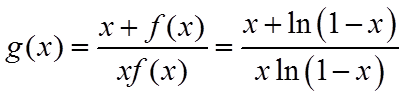
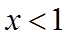
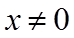
当 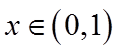
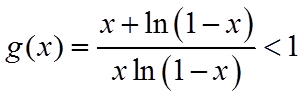
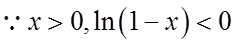
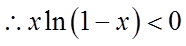
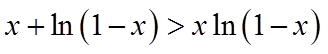
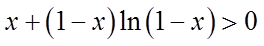
同理,当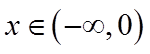
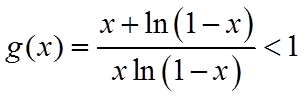
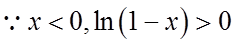
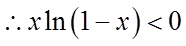
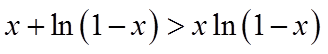
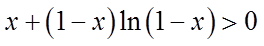
令

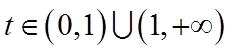
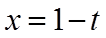
令
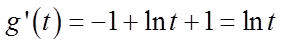
当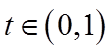
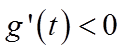
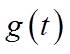
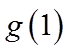
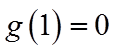
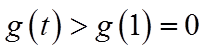
当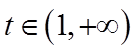
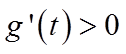

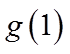
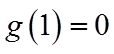
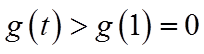
综上所述,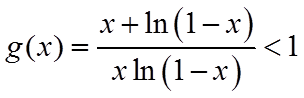
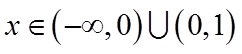
【点睛】本题为难题,根据极值点处导数为0可求参数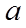
21. 已知抛物线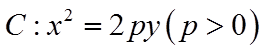
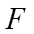
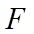
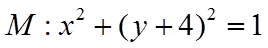
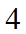
(1)求
(2)若点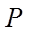
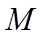
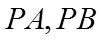
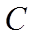
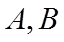
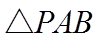
正确答案
(1)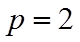
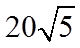
解析
(1)根据圆的几何性质可得出关于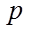
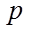
(2)设点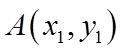
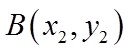
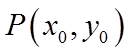
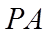
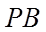
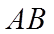
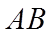
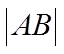
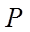
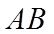
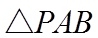
【详解】(1)抛物线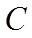
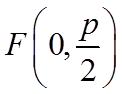
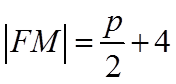
所以,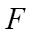
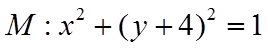
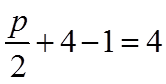
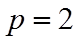
(2)抛物线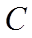
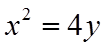
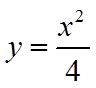
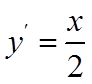
设点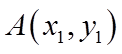
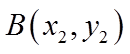
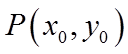
直线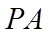
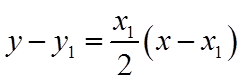
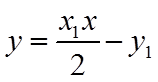
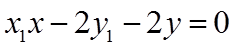
同理可知,直线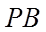
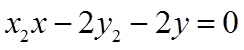
由于点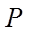
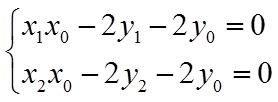
所以,点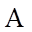
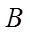
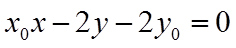
所以,直线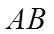
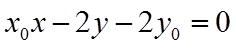
联立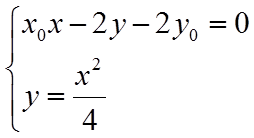
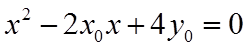
由韦达定理可得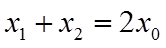
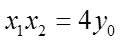
所以,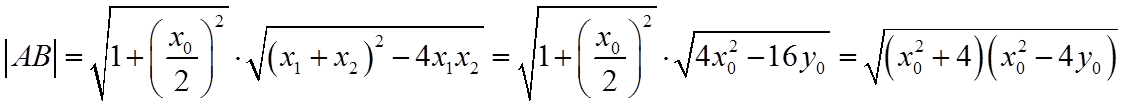
点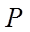

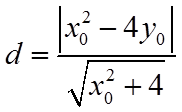
所以,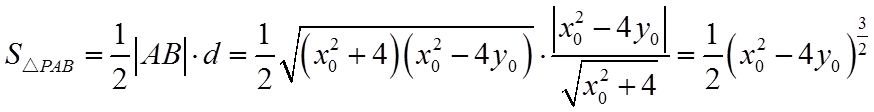
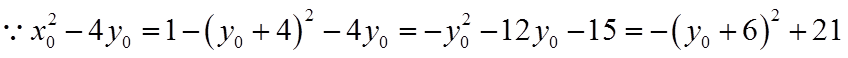
由已知可得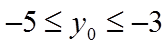
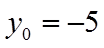
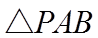
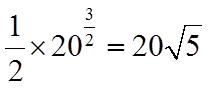
【点睛】方法点睛:圆锥曲线中的最值问题解决方法一般分两种:
一是几何法,特别是用圆锥曲线的定义和平面几何的有关结论来求最值;
二是代数法,常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题,然后利用基本不等式、函数的单调性或三角函数的有界性等求最值.
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系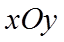
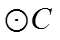
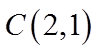
(1)写出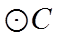
(2)过点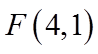
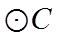
正确答案
(1)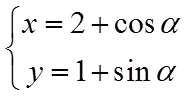
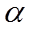
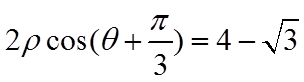
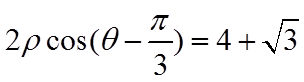
解析
(1)直接利用圆心及半径可得的圆的参数方程;
(2)先求得过(4,1)的圆的切线方程,再利用极坐标与直角坐标互化公式化简即可.
【详解】(1)由题意,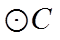
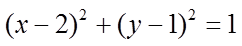
所以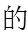
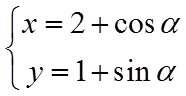
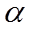
(2)由题意,切线的斜率一定存在,设切线方程为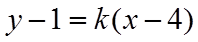
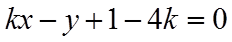
由圆心到直线的距离等于1可得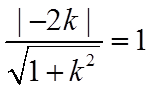
解得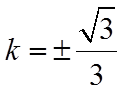
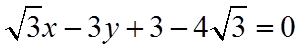
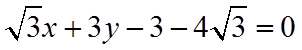
将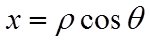
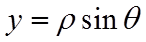
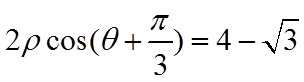
【点晴】本题主要考查直角坐标方程与极坐标方程的互化,涉及到直线与圆的位置关系,考查学生的数学运算能力,是一道基础题.
23. [选修4-5:不等式选讲](10分)
已知函数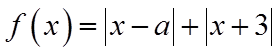
(1)当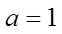
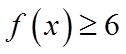
(2)若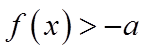
正确答案
(1)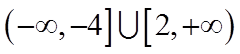
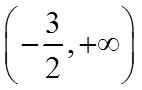
解析
(1)利用绝对值的几何意义求得不等式的解集.
(2)利用绝对值不等式化简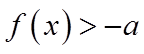
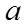
【详解】(1)当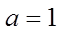
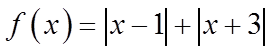
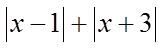
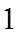
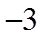
则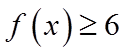
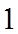
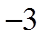
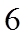
当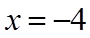
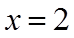
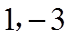
∴数轴上到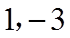
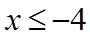
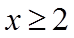
所以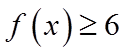
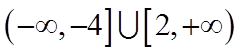
(2)依题意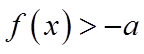
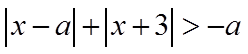
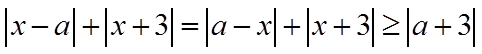
当且仅当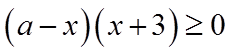
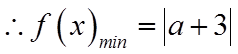
故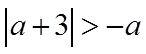
所以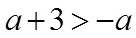
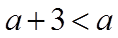
解得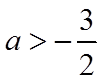
所以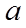
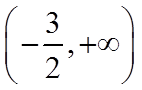
【点睛】解绝对值不等式的方法有零点分段法、几何意义法.解含有两个绝对值,且其中的