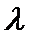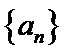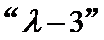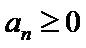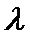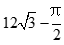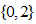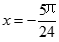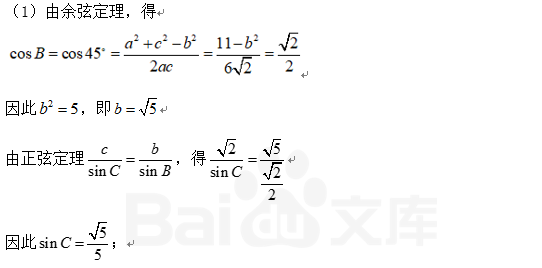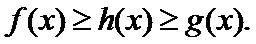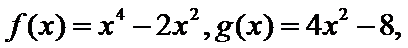- 真题试卷
- 模拟试卷
- 预测试卷
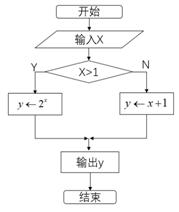
5. 右图是一个算法流程图,若输出y的值为-2,则输入x的值为 。
正确答案
-3
7.已知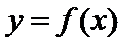
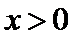
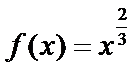
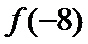
正确答案
-4
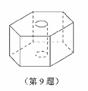
9. 如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的,已知螺帽的底面正六边形边长为2cm,高为2cm,内孔半径为0.5cm,则此六角螺帽毛坯的体积是 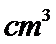
正确答案
1. 已知集合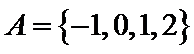
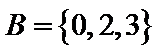
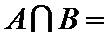
正确答案
2. 已知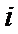
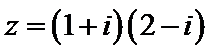
正确答案
3
3. 已知一组数据4,2a,3-a,5,6的平均数为4,则a的值是__________。
正确答案
2
4. 将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是 。
正确答案
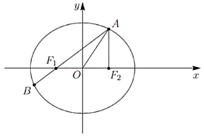
6. 在平面直角坐标系xOy中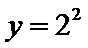
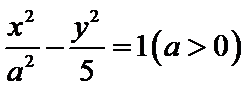
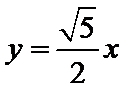
正确答案
8. 已知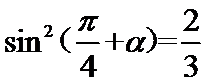
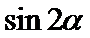
正确答案
10. 将函数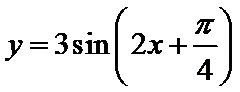
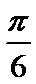
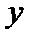
正确答案
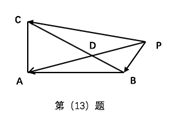
13.在△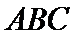
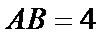
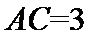
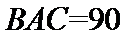
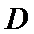
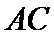
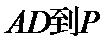
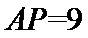
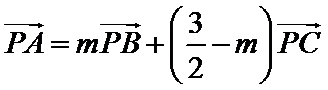
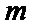
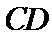
正确答案
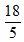
12. 已知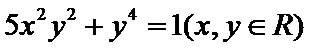
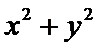
正确答案
11. 设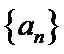
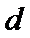
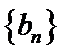
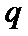
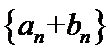
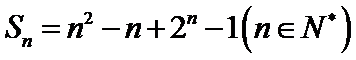
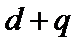
正确答案
4
14.在平面直角坐标系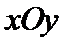
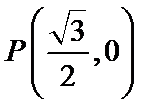
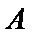
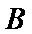
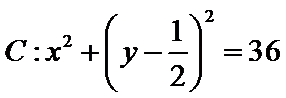
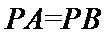
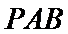
正确答案
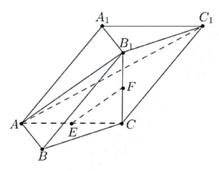
15. 在三棱柱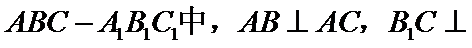
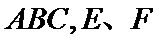
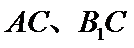
(1) 求证: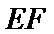
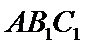
(2) 求证:平面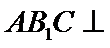
正确答案
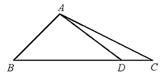
16.在△ABC中,角A、B、C的对边分别为a、b、c,已知a=3,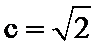
(1)求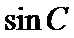
(2)在边BC上取一点D,使得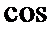
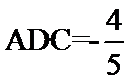
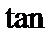
正确答案
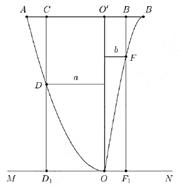
17. 某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底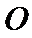
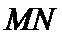
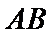
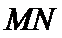
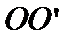
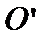
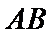
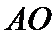
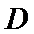
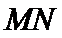
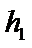
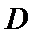
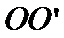
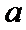
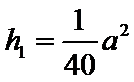
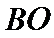
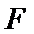
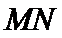
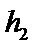
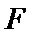
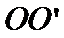
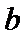
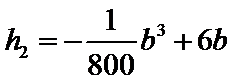
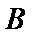
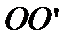
(1)求桥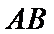
(2)计划在谷底两侧建造平行于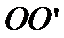
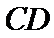
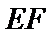
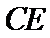
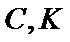
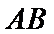
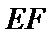
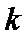
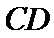
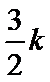
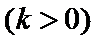
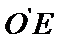
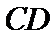
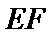
正确答案
18. 在平面直角坐标系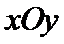
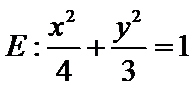
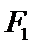
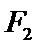
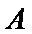
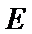
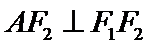
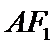
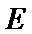
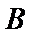
(1) 求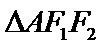
(2) 在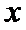
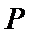
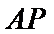
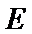
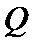
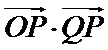
(3) 设点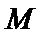
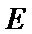
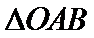
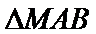
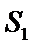
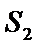
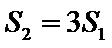
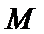
正确答案
19.已知关于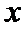
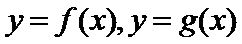
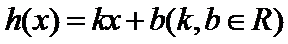
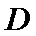
(1) 若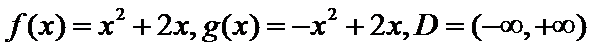
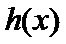
(2) 若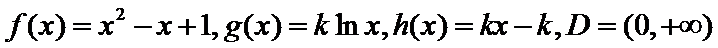
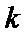
(3) 若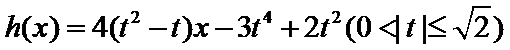
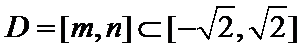
正确答案
(1)若等差数列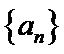
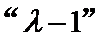
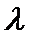
(2)若数列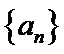
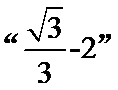
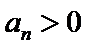
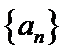
(3)对于给定的