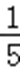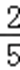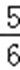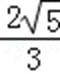- 真题试卷
- 模拟试卷
- 预测试卷
5.设


正确答案
解析

令




知识点
10.数列


正确答案
解析
∵an=a1qn-1,bn=b1+(n-1)d,a6=b7 ,∴a1q5=b1+6d,a3+a9=a1q2+a1q8 , b4+b10=2(b1+6d)=2b7=2a6,a3+a9-2a6=a1q2+a1q8-2a1q5=a1q8-a1q5-(a1q5-a1q2)=a1q2(q3-1)2≥0,所以,a3+a9≥b4+b10,故选B。
知识点
12.已知函数




正确答案
解析
如图是函数






知识点
3.由y=f(x)的图象向左平移

正确答案
解析
略。
知识点
4.已知函数

正确答案
解析



知识点
1.已知复数

正确答案
解析

知识点
6.如图, 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积为( )
正确答案
解析
由题意,棱锥的高为


知识点
7.已知函数f(x)=
正确答案
解析
∵函数f(x)=

知识点
8.若实数x,y满足的约束条件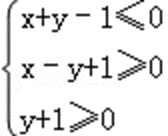
正确答案
解析
画出不等式组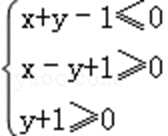
∵函数z=2ax+by在点(2,﹣1)处取得最大值,
∴直线z=2ax+by的斜率k=
∵一颗骰子投掷两次分别得到点数为(a,b),则这样的有序整数对共有6×6=36个
其中2a≤b的有(1,1),(1,2),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)共30个,
则函数z=2ax+by在点(2,﹣1)处取得最大值的概率为 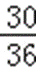
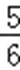
知识点
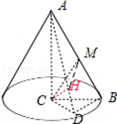
9.等腰Rt△ACB,AB=2,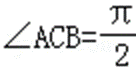
正确答案
解析
根据题意,得
∵AC⊥平面BCD,BD⊂平面BCD,∴AC⊥BD,
∵CD⊥BD,AC∩CD=C,∴BD⊥平面ACD,可得BD⊥CH,
∵CH⊥AD,AD∩BD=D,∴CH⊥平面ABD,可得CH⊥AB,
∵CM⊥AB,CH∩CM=C,∴AB⊥平面CMH,
因此,三棱锥C﹣HAM的体积V=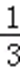
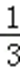
设∠BCD=θ,则Rt△BCD中,BC=
可得CD=
Rt△ACD中,根据等积转换得CH=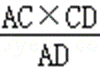
Rt△ABD∽Rt△AHM,得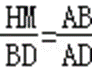
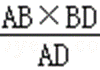
因此,S△CMH=
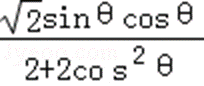
∵4+2tan2θ≥4
∴S△CMH=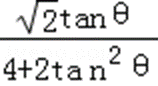
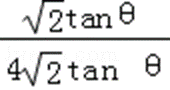
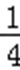
当且仅当tanθ=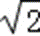
∵tanθ=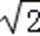
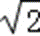
∴结合sin2θ+cos2θ=1,解出cos2θ=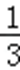
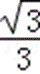
由此可得CD=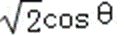

即当三棱锥C﹣HAM的体积最大时,CD的长为
知识点
2.全集



正确答案
解析


知识点
11.定义域为R的偶函数f(x)满足∀x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18.若函数y=f(x)﹣loga(x+1)至少有三个零点,则a的取值范围是( )
正确答案
解析
∵f(x+2)=f(x)﹣f(1),且f(x)是定义域为R的偶函数,
令x=﹣1可得f(﹣1+2)=f(﹣1)﹣f(1),f(﹣1)=f(1),
即 f(1)=0 则有,f(x+2)=f(x),
∴f(x)是周期为2的偶函数。
当x∈[2,3]时,f(x)=﹣2x2+12x﹣18=﹣2(x﹣3)2,
函数的图象为开口向下、顶点为(3,0)的抛物线。
∵函数y=f(x)﹣loga(|x|+1)在(0,+∞)上
至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至少有3个交点。
∵f(x)≤0,∴g(x)≤0,可得a<1。
要使函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
则有g(2)>f(2),可得 loga(2+1)>f(2)=﹣2,
∴loga3>﹣2,∴3<


又a>0,∴0<a<
知识点
13.(
正确答案
6
解析
设第
知识点
14.椭圆
正确答案
解析
因为椭圆


知识点
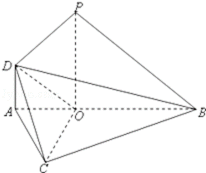
18.如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=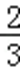
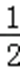
(1)求证:PD⊥平面COD;
(2)求二面角B﹣DC﹣O的余弦值。
正确答案
见解析。
解析
(1)证明:设OA=1,则PO=OB=2,DA=1,
由DA∥PO,PO⊥平面ABC,知DA⊥平面ABC,
∴DA⊥AO,从而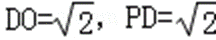
在△PDO中,∵PO=2,
∴△PDO为直角三角形,故PD⊥DO。
又∵OC=OB=2,∠ABC=45°,
∴CO⊥AB,又PO⊥平面ABC,
∴PO⊥OC,
又PO,AB⊂平面PAB,PO∩AB=O,
∴CO⊥平面PAB。
故CO⊥PD。
∵CO∩DO=O,
∴PD⊥平面COD。
(2)解:以OC,OB,OP所在射线分别为x,y,z轴,建立直角坐标系如图。
则由(1)知,C(2,0,0),B(0,2,0),P(0,0,2),D(0,﹣1,1),
∴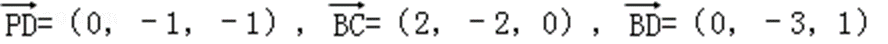
由(1)知PD⊥平面COD,∴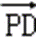
设平面BDC的法向量为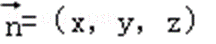
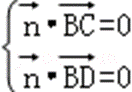
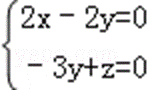
令y=1,则x=1,z=3,∴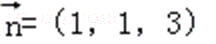
∴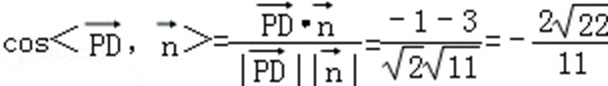
由图可知:二面角B﹣DC﹣O为锐角,二面角B﹣DC﹣O的余弦值为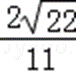
知识点
15.已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
(1)求数列{an}的通项公式;
(2)若bn=

正确答案
(1)an=2n
(2)n的最小值为5
解析
(1)设等比数列{an}的首项为a1,公比为q,
依题意,有2(a3+2)=a2+a4,
代入a2+a3+a4=28, 得a3=8,
∴a2+a4=20
∴

又{an}单调递增,∴q=2,a1=2,
∴an=2n
(2)
∴
∴
∴①-②得
∴
故使
知识点
17.在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2c- a)cosB- bcos A=0。
(1)求角B的大小
(2)求
正确答案
(1)
(2)
解析
(1)

(2)由(1)知


知识点
20.已知动圆












(1)求曲线
(2)试探究

(3)记





正确答案
见解析。
解析
(1)设圆心

由于动圆


圆





故圆心

(2)设

由

由


(3)




令







知识点
21.已知

(1)

(2)记


(3)是否存在


正确答案
见解析。
解析
(1)
(2)当0≤x≤t时,f(x)=

因此,当x∈(0,t)时,f′(x)=
当x∈(t,+∞)时,f′(x)=
①若t≥6,则f(x)在(0,6)上单调递减,g(t)=f(0)=
②若0<t<6,则f(x)在(0,t)上单调递减,在(t,6)上单调递增。
所以g(t)=mtx{f(0),f(6)}。
而f(0)-f(6)=

当2<t<6时,g(t)=f(0)=
(3)由(1)知,当t≥6时,f(x)在(0,6)上单调递减,故不满足要求。
当0<t<6时,f(x)在(0,t)上单调递减,在(t,6)上单调递增。
若存在x1,x2∈(0,6)(x1<x2),使曲线y=f(x)在(x1,f(x1)),(x2,f(x2))两点处的切线互相垂直,则x1∈(0,t),x2∈(t,6),且f′(x1)·f′(x2)=-1,
即

由x1∈(0,t),x2∈(t,6)得x1+3t∈(3t,4t),

故(*)成立等价于集合T={x|3t<x<4t}与集合B=



综上所述,存在t使函数f(x)在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直,且t的取值范围是
知识点
16.已知函数

(1)求函数
(2)已知







正确答案
(1)


(2)
解析
(1)

由




(2)∵

∵


即

由余弦定理

即
∴
知识点
19.为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽样100名志原者的年龄情况如下表所示。
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图)再根据频率分布直方图估计这500名志愿者中年龄在 [30,35)岁的人数;
(2)在抽出的100名志原者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学 期望
正确答案
见解析。
解析
(1)0.2×100=20,
∴①处是20,②处是0.35,
∵由频率分步直方图中,[30,35)的人数是0.35×500=175
在频率分步直方图知,在[25,30)这段数据上对应的频率是0.2,
∵组距是5,
∴小正方形的高是
在频率分步直方图中补出高是0.04的一个小正方形。
(2)用分层抽样方法抽20人,
则年龄低于30岁的有5人,年龄不低于30岁的有15人,
故X的可能取值是0,1,2,
P(X=0)=

∴X的分布列是
∴X的期望值是EX=