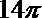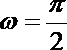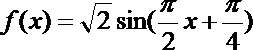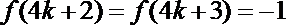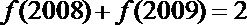- 真题试卷
- 模拟试卷
- 预测试卷
2.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.计算:
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
6. 

正确答案
45
解析
解析已在路上飞奔,马上就到!
知识点
7.关于

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知平面向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.无穷数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在某地奥运火炬传递活动中,有编号为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.一个长方体的各个顶点均在同一球面上,且一个顶点上的三条棱长分别为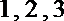
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数 ①







正确答案
②
解析
解析已在路上飞奔,马上就到!
知识点
13.求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.对


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如下图,根据该流程图,可以得出该算法的功能是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在数列



① 在差等比数列中
② 等差数列一定是差等比数列
③ 等比数列一定是差等比数列
④差等比数列中可以有无数项为
其中正确的判断是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设二次函数



(1)求函数
(2)若对于任意的


正确答案
(1)设
∵ 

∴
(2)
∴
即
解析
解析已在路上飞奔,马上就到!
知识点
21.已知抛物线



(1)求椭圆的标准方程;
(2)设





正确答案
(1)焦点


∴ 椭圆的方程为
(2)设
∴
当
当

∴
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列




(1)能否唯一确定数列

(2)能否求得
(3)若





正确答案
(1)
即
由于

因此不能唯一确定数列
(2)为使
为使

∴ 


(3)

∴ 

∴
解析
解析已在路上飞奔,马上就到!
知识点
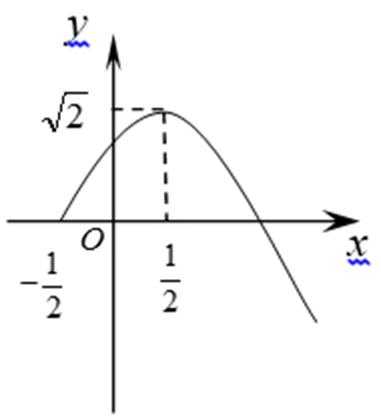
19.若函数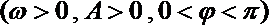
(1)求出函数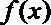
(2)求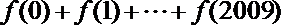
正确答案
(1)由图知:
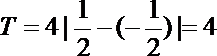
∴ 
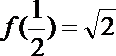
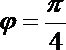
∴
(2)由(1)得 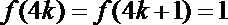
∴ 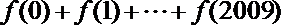
解析
解析已在路上飞奔,马上就到!
知识点
22.对于函数








(1)判断函数
(2)已知







(3)在(2)的条件下,令

正确答案
(1)
∴
∴ 是“幅度函数”,其“幅度”为2
(2)
∵ 


∴ 当
当
∴ 
∴
(3)
令

∴
解析
解析已在路上飞奔,马上就到!