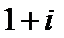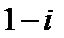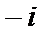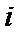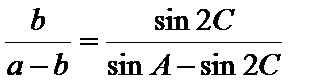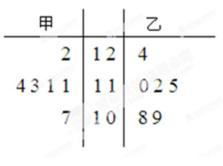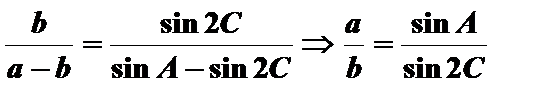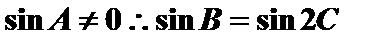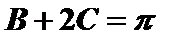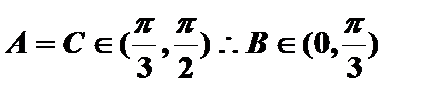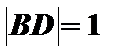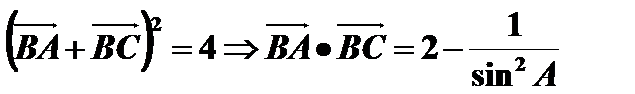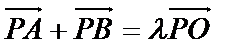- 真题试卷
- 模拟试卷
- 预测试卷
2.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如下程序框图的功能是:给出以下十个数:5,9,80,43,95,73,28,17,60,36,把大于60的数找出来,则框图中的①②应分别填入的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知复数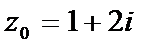
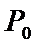
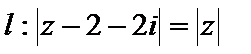
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知以下三视图中有三个同时表示某一个三棱锥,则不是该三棱锥的三视图是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.集合A=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在平面直角坐标系中,不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知以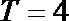
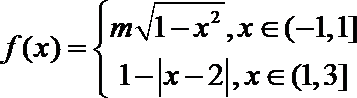
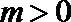
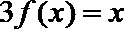
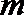
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若三棱锥



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设二次函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
16.给出下列四个命题:
①
②

③







④在


其中正确命题的序号是( )
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
13.公比为4的等比数列











正确答案
300
解析
解析已在路上飞奔,马上就到!
知识点
18.某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品
(1)根据样本数据,计算甲、乙两个车间产品重量的均值与方差,
(2)若从乙车间6件样品中随机抽取两件,求所抽取两件样品重量之差不超过2克的概率.
正确答案
(1)甲相对稳定。


(2)从乙车间6件样品中随机抽取两件,共有15种不同的取法:(108,109),
(108,110),(108,112),(108,115),(108,124),(109,110),
(109,112),(109,115),(109,124),(110,112),(110,115),
(110,124),(112,115),(112,124),(115,124).
设A表示随机事件“所抽取的两件样品的重量之差不超过2克”,
则A的基本事件有4种:(108,109),(108,110),(109,110),(110,112).
故所求概率为P(A)=
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23题中任选一题作答。若多做,则按所做的第一题计分。
22.已知点



(1)求在直角坐标系中点

(2)求
23.已知函数
(1)若

(2)若满足

正确答案
22.
(1)设点P的坐标为(x,y),则有
由于α∈[0,π],∴y≥0,故点P的轨迹是上半圆
∵曲线C:

故曲线C的直角坐标方程:x-y+10=0.
(2)由题意可得点Q在直线x-y+10=0 上,点P在半圆上,半圆的圆心C(1,0)到直线x-y+10=0的距离等于
即|PQ|的最小值为
23.
解:(Ⅰ)


(Ⅱ)由(Ⅰ)可知,


当

当

当


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)求函数
(2)若以函数



(3)是否存在实数



正确答案
解:(I)
∵



由


∴


(II)

当



(III)若



令
则
当x变化时,

由表格知:
画出草图和验证



∴当


解析
解析已在路上飞奔,马上就到!
知识点
17.在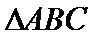
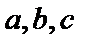
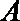
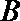
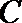
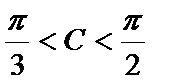
(1)判断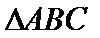
(2)若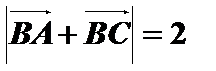
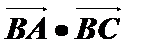
正确答案
解:(1)由题意
由正弦定理知,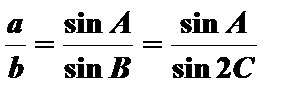
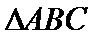
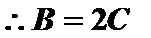
当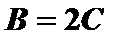
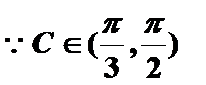
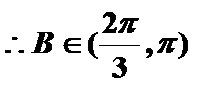

当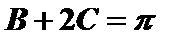
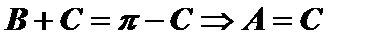
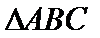
(2)在等腰三角形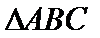
取AC中点D,由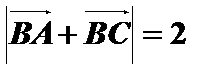
又由,
所以,
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知点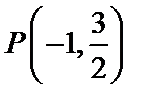
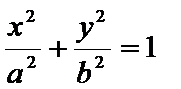

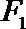
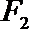
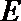
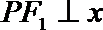
(1)求椭圆
(2)设


正确答案
解:(1)∵PF1⊥x轴,
∴F1(-1,0),c=1,F2(1,0),
|PF2|=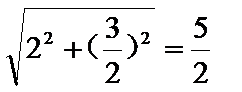
椭圆E的方程为:
(2)设A(x1,y1)、B(x2,y2),由 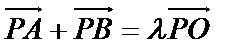
(x1+1,y1-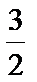
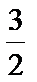
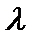
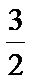
所以x1+x2=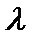
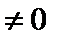
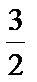
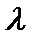
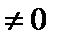
又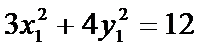
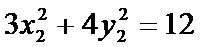
两式相减得3(x1+x2)(x1-x2)+ 4(y1+y2)(y1-y2)=0………..②
以①式代入可得AB的斜率k=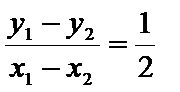
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,已知矩形













(1)求证:平面


(2)设





正确答案
(1)证明:
(2)
如图,建立坐标系,则

易知
解析
解析已在路上飞奔,马上就到!