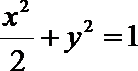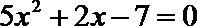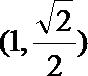- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合 A= {x |- 1<x<2},{x | 0<x<3},则 A U B( )
正确答案
解析
利用数轴,在数轴上分别表示集合A和集合B的取值范围,根据并集的概念结合图示,得到答案,所以选A
考查方向
本题主要考查集合的并集运算,体现了学生的基础知识掌握能力。常与不等式知识交汇命题。
解题思路
利用数轴,根据并集的概念,直接求出集合A和集合B 的并集,结合选项,选出正确答案
易错点
混淆交集、并集、补集的概念,不会利用数轴判断不等式取值范围
知识点
3.已知双曲线c: 


正确答案
解析
先根据离心率求出双曲线a和b的关系式,利用双曲线中a2+b2=c2 的恒等式,求得渐近线的方程,所以选C
考查方向
本题主要考查双曲线的离心率和渐近线方程,考查学生的基本知识掌握能力
解题思路
利用离心率求渐进线方程。
易错点
记混双曲线离心率以及渐近线方程的求法。
知识点
5.设Sn是等差数列{an}的前n项和,若a1+a3+a5=3 ,则S5 = (
正确答案
解析
根据关系式a1+a3+a5=3,得到a1+2d=1,,S5=5a1+10d,所以S5=5(a1+2d)=5,所以本题选A
考查方向
本题主要考查等差数列项数和项之间的关系,属于中档题,是高考的热点。
解题思路
通过前三项奇数项关系式,求出等差数列的首项和公差,利用等差数列前n项和求和公式求解。
易错点
等差数列项数和项概念混淆。
知识点
6.—个长方体被一个平面截去一部分后所剩几何体的三视图如下图所示(单位:cm),则该几何体的体积为
正确答案
解析
由三视图可判断几何体为一长方体削去一个角,其直观图如图:
长方体的长、宽、高分别为5、4、6,
∴长方体的体积为5×4×6=120,削去的三棱锥的体积为5×4×6=20,
∴该几何体的体积为120-20=100cm2.
故选C
考查方向
本题主要考查空间几何体的三视图,根据三视图还原成空间几何体求体积,中档题,体现了学生对所学知识的运用能力。
易错点
三视图概念不清楚
知识点
7.某算法的程序框图如图所示,若输人的a,b的值分别为60与32,则程序执行后的结果是( )
正确答案
解析
根据题意,模拟程序框图的运行过程,用辗转相除法求两个数a、b的最大公约数;当a=60,b=32时,最大公约数是4.故选:B
考查方向
本题主要考查算法的程序框图,体现了学生的基础知识掌握能力。
解题思路
按照流程图分布计算即可。
易错点
对程序流程理解错误。
知识点
9.设实数x,y;满足
正确答案
解析
作出不等式组对应的,则xy=12•(2x•y)≤12(2x+y2)2=252, 当且仅当2x=y=5,利用基本不等式进行求解即可,所以选A
考查方向
本题主要平面区域不等式的基本性质,考查学生数形结合的能力。
解题思路
本题考查并集的运算。
易错点
不理解基本不等式概念,不能转换成基本不等式求解。
知识点
10.点A,B,C,D在同一个球的球面上,AB = B
正确答案
解析
AB=BC=AC=√3
∴四面体ABCD体积最大时,D在ABC的另一个半球内正△ABC面积=3√3/4
∴高=4
∴D到面ABC距离=4ABC所在面的圆心为O'球心为O
∴O'A=O'B=O'C=2√3×√3×sin60°=1设球的半径为R勾股定理得(4-R)²+1²=R²
解得R=17/8
∴表面积=4πR²=289/16
考查方向
本题主要与球体有关的计算、四面体体积最值问题。属于较难题
解题思路
先找到四面体体积最大时球的半径,然后再求表面积
易错点
找不到四面体体积最大时的情况,忘记球表面积计算公式
知识点
2.i是虚数单位,复数 
正确答案
解析
分子分母同时乘以分母的共轭复数2-5i,分母变成29,分子变成(5-2i)(2-5i)化简分子得-29i,结合选项,可得出答案,所以选C
考查方向
本题主要考查复数的运算,考查学生对基础知识掌握能力。
解题思路
根据复数的运算法则,将复数化简,然后结合选项选出正确答案。
易错点
复数的乘除法运算,对虚数概念的理解。
知识点
4.已知向量a = (1,一 1),向量b=(-1,2),则(2a +b)• a = ( )
正确答案
解析
先求出向量2a+b的坐标表示,2a+b=(1,0),然后根据向量数量积运算法则,得到(2a+b)a=1+0=1,所以选C
考查方向
本题主要考查向量的加法运算、平面向量数量积的运算律,体现了学生的基础知识掌握能力。
解题思路
先计算向量加法,再根据向量坐标计算向量数量积。
易错点
记混平面向量数量积运算律
知识点
8.已知

正确答案
解析
a3a5=a42 =4(a4-1),解得a4=2,所以q3=a4/a1=8,推出q=2.故a2=a1q=1/2,所以选C
考查方向
本题主要考查等比数列项数与项的概念和关系,属于中档题。
解题思路
利用所给条件求出公比q,进而求出等比数列的第2项。
易错点
对等比数列公比q 的理解错误
知识点
11.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲,乙,丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是 ( )
正确答案
解析
“燃油效率”是指汽车每消耗1升汽油行驶的里程,A中乙车消耗1升汽油,最多行驶的路程为乙车图象最高点的纵坐标值,A错误;
B中以相同速度行驶相同路程,甲燃油效率最高,所以甲最省油,B错误,
C中甲车以80千米/小时的速度行驶1小时,甲车每消耗1升汽油行驶的里程10km,行驶80km,消耗8升汽油,C错误,
D中某城市机动车最高限速80千米/小时. 由于丙比乙的燃油效率高,相同条件下,在该市用丙车比用乙车更省油,选D.
考查方向
函数应用问题;对“燃油效率”新定义的理解;对图象的理解。
解题思路
根据新定义的概念,做出图象求解
易错点
不理解新定义的概念,对函数图象理解不透彻
知识点
12.已知函数F(x) = 




正确答案
解析
利用函数的奇偶性得到g(x)=
h(x)=

则t在[1,2]上单调递增,
所以

考查方向
本题主要考查函数的基本性质,此类试题是高考的重点题型,长和方程不等式交叉考查,属于较难题型。
解题思路
本题考查并集的运算。
易错点
对函数的奇偶性、单调性理解不透彻
知识点
13.给出下列命题:
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②由变量x和y的数据得到其回归直线方程L:y =bx + a,则L一定经过点P(x,y)
③从匀速传递的产品生产流水线上


④在回归分析模型中,残差平方和越小,说明模型的拟合效果越好;
⑤在回归直线方程y = 0.lx + 10中,当解释变量x每增加一个单位时,预报变量y增加0.1 个单位,
其中真命题的序号是 .
正确答案
②④⑤
解析
①线性相关系数|r|越大,两个变量的线性相关性越强,故①不正确;
②由变量x和y的数据得到其回归直线方程l:y=bx+a,则l一定经过点P故②正确;
③从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样不是分层抽样,故③不正确;
④可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故④正确;
⑤在回归直线方程y=0.1x+10中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位,故⑤正确.
故答案为:②④⑤
考查方向
本题线性相关、回归直线方程和拟合等相关概念。
易错点
对上述概念理解的不透彻
知识点
14.在三棱锥S—ABC内任取一
正确答案
解析
如图所示,只有当P点为SO的中点,即当P在三棱锥的中截面与下底面构成的三棱台内时,符合要求。所以填
考查方向
概率、三棱锥的体积的求法。
易错点
不会计算三棱锥体积,不理解相关概率的意义
知识点
15.已知圆 C : (x —3)2 + (y — 4) 2= 1 和两点 A (-m,0),B(m,0) (m>0),若圆上存在点 P,使得 ∠APB = 90°,则m的取值范围是 .
正确答案
[4,6]
解析
圆心C(3,4),半径r=1,AP垂直BP,所以(a+m)(a-m)+b2=0,即m2=a2+b2,所以OP的最大值为OC+r=5+1=6,最小值为4,所以填[4,6].
考查方向
圆的方程,两点间距离公式,最值问题。
解题思路
利用向量垂直时的数量积关系,将m转换成求OP的最大值
易错点
找不到m在圆中所代表的含义,不会运用转换思想。
知识点
16.已知曲线x在
正确答案
6
解析
y=x+lnx的导数为y′=1+1/x,曲线y=x+lnx在x=1处的切线斜率为k=2,
则曲线y=x+lnx在x=1处的切线方程为y-1=2x-2,即y=2x-1.由于切线与曲线y=ax2+(a+2)x+1相切,故y=ax2+(a+2)x+1可联立y=2x-1,得ax2+ax+2=0,又a≠0,两线相切有一切点,所以有△=a2-8a=0,解得a=8.故答案为:8.
考查方向
曲线的切线方程,导数的几何意义
解题思路
先求出曲线在切点处的切线方程,然后联立成方程组,化成一元二次方程,利用根的判别式求解。
易错点
导数的几何意义理解的不透彻,不会求切点。
知识点
19.已知在四棱锥S—ABCD中,底面ABCD是平行四边形,若SB丄AC,SA = SC.
(1)求证:平面SBD丄平面
(2)若 AB = 2,SB = 3,cos∠SCB=
正确答案
如图所示
(1)设AC∩BD=O,
连接SO
因为SA=SC,
所以SO∩SB=S,所以AC⊥平面SBD,
因为AC在平面ABCD内,
所以平面SBD⊥平面ABCD
(2)作SH⊥平面ABCD,即
由(1)知,AC⊥BD,
所以底面ABCD是菱形,
所以BC=AB=2
因为SB=3,cos∠SCB=1/8
所以由余弦定理可得,
SC=2,所以∠SAC=60°,
所以SAC是等边三角形
所以在Rt△SOH中,SH=SO*sin60°=3/2
所以
解析
证AC垂直于面ABCD,
设AC交BD于0,
因为SA=SC,
SO交SB于S,
所以AC垂直于平面SBD,
因为AC在平面ABCD内,
所以面SBD垂直于面ABCD.求底面面积时,
先用余弦定理求出角SOB=120度,角SOH=60度,
所以四棱锥的体积为
考查方向
立体几何中的相关计算和证明
解题思路
通过线线垂直得到线面垂直,进而得到面面垂直,找清四棱锥的底面和高,利用公式求解。
易错点
面面垂直概念混淆,立体感不强
知识点
21.已知函数f(x)= 

(1)求函数f(x)的单调区间;
(2)当a = l时,求f(x)在区间[
(3)求证ln
正确答案
(1)函数的定义域为
若
故





在
(2)

由(1)可知,

在区间[1,2上单调递减,
所以

而
故函数

(3)由(2)可知,
函数
故有,
解析
将f(x)求导并整理,
得到f(x)在x>0区间上单调递减,
然后分类讨论a的不同取值对单调区间的影响。
利用函数单调性证明不等式恒成立的条件。
解题步骤见答案。
考查方向
本题主要考查函数的单调性和函数的最值。
解题思路
本利用导数求单调区间,利用函数与不等式关系求最大值最小值
易错点
不会利用导数求函数单调区间。
知识点
17.在△ABC中,角A,B


(1)求角A的值;
(2)若∠B =

正确答案
(1)
得
化简得,
(2)可知三角形ABC为等边三角形,
在三角形AMC中,
由余弦定理,
可得
解得,AC=b=2,
所以,
解析


化简得,A=30度,
可知三角形ABC是等腰三角形,
由余弦定理可得,b=2,
所以面积为
考查方向
本题主要考查正弦定理和余弦定理的性质,属于基础题
解题思路
先用正弦定理求A,然后利用余弦定理求三角形的面积
易错点
混淆两个定理的性质
知识点
20.已知P为圆A:(x + l)2+y2=8上的动点,点B(1,0),线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为P.
(1)求曲线P的方程;
(2)当点P在第一象限,且COS∠BAP=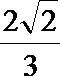
正确答案
(1)圆A的圆心为A(-1,0),半径为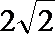
由已知得,
故曲线P是以A,B为焦点,
以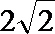
且
故曲线P的方程为
(2)由点P在第一象限,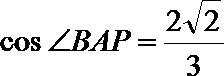
得
于是直线AP方程为:
消去y,可得,
所以,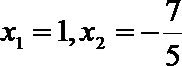
所以点M的坐标为
解析
已知圆心为A(-1,0),半径为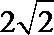
容易得到MA=MP,所以MA+MB=MA+MP,
故曲线P是以A,B为焦点,
以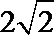
从而可求曲线方程,
当点P在第一象限,
求出点P的坐标,可得直线AP方程,
带入椭圆方程,消去y,即可得到M点的坐标。
考查方向
本题主要考查直线和圆的方程的应用
解题思路
根据已知条件求出曲线的方程,根据曲线方程求出点的坐标。
易错点
椭圆的方程定义不清楚,计算能力弱
知识点
18.某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若 干,其中合格零件的个数如下表:
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的
(2)质检部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车

正确答案
(1)依据题中的数据可得,
X甲=

所以两组技工的总体水平相同,甲组中技工的技术水平差异比乙组大。
(2)设事件A表示:该车间“质量合格”,
则从甲、乙两组中各抽取1名技工完成合格零件个数的基本事件为:(4,5)(4,6)(4,7)(4,8)(4,9)(5,5)(5,6)(5,7)(5,8)(5,9)(7,5)(7,6)(7,7)(7,8)(7,9)(9,5)(9,6)(9,7)(9,8)(9,9)(10,5)(10,6)(10,7)(10,8)(10,9)共25种,
所以概率P(A)= 17/25
解析
利用平均数和方差公式,求得甲的平均数是7,乙的平均数是7,甲的方差为5.2,乙的方差为2,两组技工的总体水平相同,甲组中技工的技术水平差异比乙组大;列出所有时间发生的基本事件,共17种,所以质量合格的概率为17/25
考查方向
本题主要考查平均数与方差的求法。考查随机事件发生的概率
解题思路
按照概念依次求解
易错点
对平均数和方差理解不透彻,不会计算随机事件发生的概率
知识点
22.已经曲线C1的参数方程为


(1)分别写出C1的普通方程,C2的直角坐标方程;
(2)已知M,N分别为曲
的最大值.
正确答案
(1)曲线C1的普通方程为
(2)由曲线C1:


由题意可知,M
因此,
所以当


解析
主要是消去参数。利用解析几何相关知识求解
考查方向
本题主要考查直角坐标和极坐标的相互转换,考察解析几何的简单应用
易错点
直角坐标和极坐标不会转换