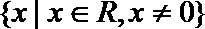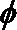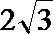- 真题试卷
- 模拟试卷
- 预测试卷
2.函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7.设椭圆的两个焦点分别为F1，F2，过F2作椭圆长轴的垂线交椭圆于点P，若三角形F1PF2为等腰直角三角形，则椭圆的离心率为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8.三角形ABC中，角A、B、C所对的边分别是
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.曲线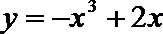
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10.当x>0时，下列函数中最小值为2的是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3.现要完成3项抽样调查
①从10盒酸奶中抽取3盒进行卫生检查；
②科技报告厅有座椅32排，每排40个座位，有一次报告会恰好坐满了观众，抽取32位进行座谈；
③某中学共有160名教职工，其中教师120名，行政人员16名，后勤人员24名，为了解教职工对校务公开方面的意见，抽取一个容量为20的样本进行调查
较为合理的抽样方法是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5.在平行四边形ABCD中，E、F分别是CD和BC的中点，若
A
B1
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6.一个空间几何体的三视图如下，则它的体积是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.下列四个命题中真命题是（ ）
P1：
P2：
P3：
P4：
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1.设集合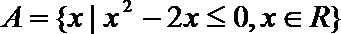
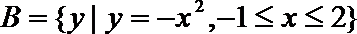
AR
B
C{0}
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11.过原点且倾斜角为60度的直线被圆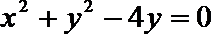
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13.设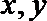
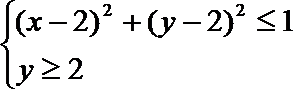
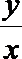
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12.设复数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
选做题14----15，只能从中选做一题
14. 极坐标方程为
15. 如图所示，圆O上一点C在直径AB上的射影为D，CD=4，BD=8，则圆O的半径等于_______.
正确答案
14.
15. 5
解析
解析已在路上飞奔，马上就到！
知识点
18.如图，四面体ABCD中，O是BD的中点，CA=CB=CD=BD=2，AB=AD=
（1）求证：AO⊥平面BCD；
（2）求E到平面ACD的距离；
（3）求异面直线AB与CD所成角的余弦值。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21.已知函数
（1）试用
（2）若
（3）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
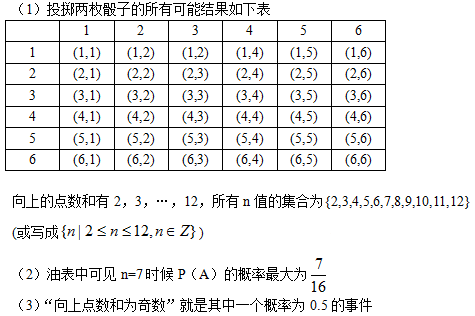
16.掷两枚骰子，记事件A为“向上的点数之和为n”.
（1）求所有n值组成的集合；
（2）n为何值时事件A的概率P(A)最大？最大值是多少？
（3）设计一个概率为0.5的事件（不用证明）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19.设函数
（1）当
（2）若函数f(x)在（0,1]上是增函数，求实数
（3）是否存在实数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17.如图，有三个并排放在一起的正方形，
（1）求
（2）求函数
17.如图，有三个并排放在一起的正方形，
（1）求
（2）求函数
的最大值及取得最大值时候的x值。
正确答案
20.在
（1）求曲线E的方程；
（2）是否存在直线L，使L与曲线E交于不同的两点M、N，且线段MN恰被直线
正确答案
解析
解析已在路上飞奔，马上就到！