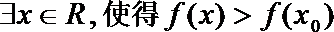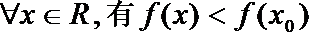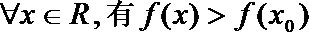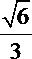- 真题试卷
- 模拟试卷
- 预测试卷
2．“
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．若集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．为了得到函数
A向右平移
B向左平移
C向右平移
D左平移
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．下列四类函数中，满足性质“对任意的实数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知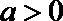
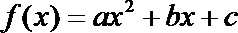
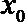
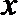
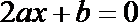
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知向量
A0
B
C4
D8
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．如右图所示，一个对称图形做的薄片（其对称轴与水面垂直）匀速地升出水面，记t时刻该薄片露出水面部分的图形面积为
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．已知
正确答案
4
解析
解析已在路上飞奔，马上就到！
知识点
17．函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．在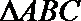
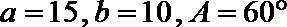
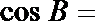
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知
正确答案
(0,
解析
解析已在路上飞奔，马上就到！
知识点
11．已知A．B均为集合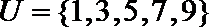
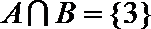
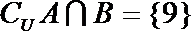
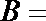
正确答案
{3,9}
解析
解析已在路上飞奔，马上就到！
知识点
13．函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．对于实数x．y，定义新运算
正确答案
2010
解析
解析已在路上飞奔，马上就到！
知识点
18．已知m>0，设命题
正确答案
解：若p真，则
若p真q假，则：
若p假q真，则：
综上：
解析
解析已在路上飞奔，马上就到！
知识点
20．已知函数
（1）画出函数在
（2）写出函数的最小正周期和单调递增区间；并求：当x为何值时，函数有最大值？最大值是多少？
（3）若x是△ABC的一个内角，且y2＝1，试判断△ABC的形状。
正确答案
(1)∵y＝|cosx＋sinx|＝，
当x∈时，其图象如图所示．
(2)函数的最小正周期是π，其单调递增区间是： (k∈Z)．
由图象可以看出，当x＝kπ＋(k∈Z)时，该函数的最大值是.
(3)若x是△ABC的一个内角，则有0＜x＜π，
∴0＜2x＜2π.由y2＝1，得|cosx＋sinx|2＝1，即：1＋sin2x＝1.
∴sin2x＝0，∴2x＝π，x＝，故△ABC为直角三角形．
解析
解析已在路上飞奔，马上就到！
知识点
21． 设函数
(1)求函数
(2)试探究函数
正确答案
（1）函数
（2）假设函数
即：
解析
解析已在路上飞奔，马上就到！
知识点
22．已知
(1)当
(2)若函数
(3)函数
正确答案
(3) 若函数
即
故函数
若函数
即
而
故函数
综上可知函数
解析
解析已在路上飞奔，马上就到！
知识点
19．在平面直角坐标系xoy中，点
(1)求以线段AB．AC为邻边的平行四边形两条对角线的长；
(2)设实数t满足
正确答案
(1)
所以
故所求的两条对角线的长分别为
（2）由题设知：
由
从而
解析
解析已在路上飞奔，马上就到！