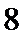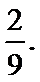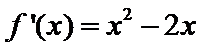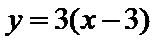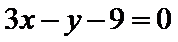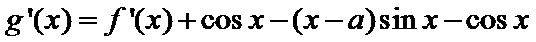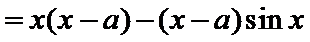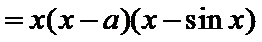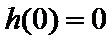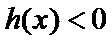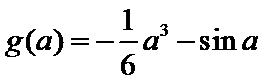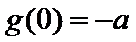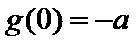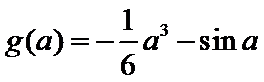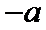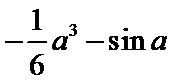- 真题试卷
- 模拟试卷
- 预测试卷
2.已知i是虚数单位,若复数z满足

正确答案
解析
由



考查方向
解题思路
直接利用复数的幂运算,化简求解即可
易错点
复数的幂运算,计算能力
3.已知x,y满足约束条件
正确答案
解析
画出约束条件表示的可行域,如图中阴影部分所示,平移目标函数直线,可知当其经过直线


考查方向
解题思路
由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案
易错点
数形结合的解题思想方法
4.已知

正确答案
解析
由

考查方向
解题思路
根据二倍角余弦公式,结合角的取值范围,求解答案.
易错点
相关概念记忆混淆,计算能力弱
5.已知命题p:

正确答案
解析
由






考查方向
解题思路
先分别判断两个命题的真假,然后结合选项判断答案正确与否
易错点
逻辑关系混乱
6.执行下面的程序框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( )
正确答案
解析
输入



考查方向
解题思路
通过观察程序框图,分析为填判断框内判断条件,按照题意填入判断框即可
易错点
通过对程序框图的分析对判断框进行判断
7.函数
正确答案
解析
因为

考查方向
解题思路
先换成三角函数的一般形式,然后判断其最小正周期
易错点
化简过程中有错误,不会判断三角函数的周期性
8.如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
正确答案
解析
由题意,甲组数据为56,62,65,





考查方向
解题思路
先求出两组数据的平均数和中位数,令他们分别相等,然后求出最后的值
易错点
对茎叶图不了解
10.若函数



正确答案
解析
对于A,令



考查方向
解题思路
根据所给函数的性质,结合选项依次判断求解
易错点
阅读能力弱,学习新知识能力弱
1.设集合

正确答案
解析
由


考查方向
解题思路
先解出集合M,然后求集合的交集运算
易错点
集合的运算记忆混淆
9.设


正确答案
解析
由








考查方向
解题思路
根据自变量的取值范围,带入相应的分段函数中,然后计算求解
易错点
判断函数时,不清楚
11.已知向量a=(2,6),b=


正确答案
解析
由
考查方向
解题思路
根据向量平行得到等量关系,求出参数的值
易错点
不能通过向量平行推出等量关系
14.已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当

正确答案
解析
由f(x+4)=f(x-2)可知,


考查方向
解题思路
根据所给条件,判断函数为周期函数,然后判断出函数周期,进而求解答案
易错点
对偶函数的性质掌握不好
15.在平面直角坐标系xOy中,双曲线

正确答案
解析
由抛物线的定义可得,
因为
所以渐进线方程为
考查方向
解题思路
根据抛物线的性质,得到等连关系,然后判断双曲线的渐近线方程
易错点
推理换算能力弱
12.若直线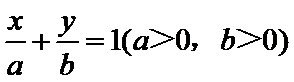
正确答案
解析
由直线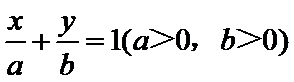
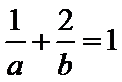
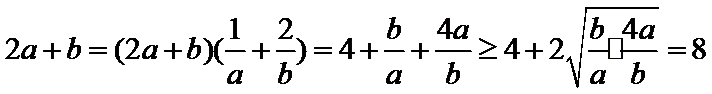
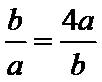
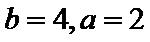
考查方向
解题思路
先根据直线过固定的点,建立等量关系,然后变形成平均值不等式形式,利用平均值不等式,求出最小值.
易错点
等号成立时的条件
13.由一个长方体和两个
正确答案
解析
由三视图可知,长方体的长、宽、高分别为2,1,1,圆柱的高为1,底面圆半径为1,所以

考查方向
解题思路
根据三视图判断出立体图形的形状,然后根据体积公式计算
易错点
判断几何体的形状及三视图的数据所对应的几何量
17.(本小题满分12分)
在


正确答案
解析
考查方向
解题思路
根据所给条件,结合正弦定理,余弦定理求解出答案
易错点
对相关定理公式记忆混淆
19.(本小题满分12分)
已知

(Ⅰ)求数列
(Ⅱ)



正确答案
(Ⅰ)
解析
(i) 设


又

(II)由题意知:
又

令

又
两式相减得
所以
考查方向
解题思路
(1)利用等比数列的通项公式求解通项公式(2)错位相减法求和
16. (本小题满分12分)
某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
正确答案
(Ⅰ)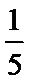
解析
(Ⅰ)由题意知,从6个国家中任选两个国家,其一切可能的结果组成的基本事件有:
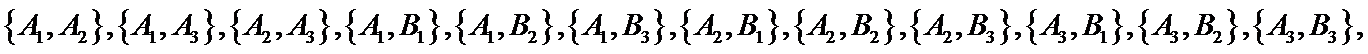
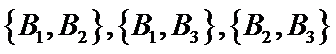
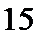
所选两个国家都是亚洲国家的事件所包含的基本事件有:
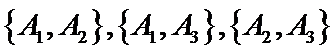
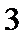
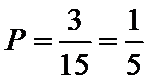
(Ⅱ)从亚洲国家和欧洲国家中各任选一个,其一切可能的结果组成的基本事件有:
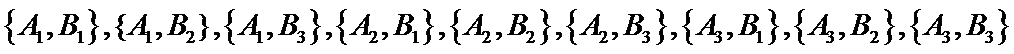
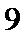
包含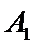
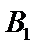
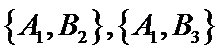
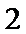
所以所求事件的概率为: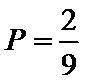
考查方向
解题思路
根据概率的相关性质和求法,求解答案
易错点
判断基本事件时,有重漏的情况.
18.(本小题满分12分)
由四棱柱ABCD-A1B1C1D1截去三棱锥C1- B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E
(Ⅰ)证明:
(Ⅱ)设M是OD的中点,证明:平面A1EM
正确答案
(Ⅰ)证明见解析.(Ⅱ)证明见解析.
解析
(1) 取




所以

因此四边形
所以






(II)因为
所以
又

所以


所以
又

所以平面

考查方向
解题思路
(1)利用线线平行,证明线面平行(2)利用线面垂直,证明面面垂直
易错点
空间想象能力弱,计算能力弱
20.(本小题满分13分)
已知函数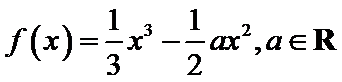
(Ⅰ)当a=2时,求曲线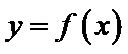
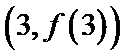
(Ⅱ)设函数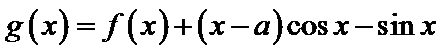
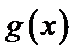
正确答案
(Ⅰ)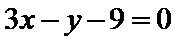
解析
(I) 由题意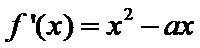
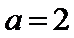
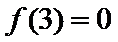
所以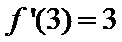
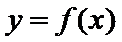
即
(II) 因为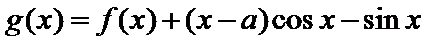
令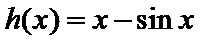
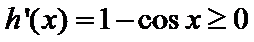
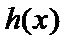
所以,当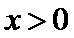
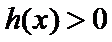
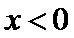
(1)当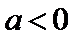
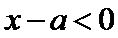
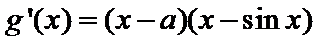
所以当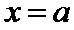
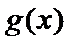
当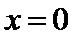
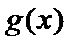
(2)当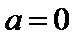
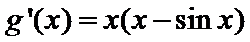
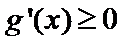
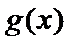
(3)当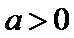
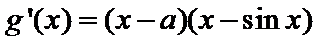
所以当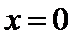
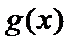
当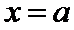
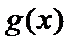
综上所述,
当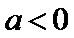
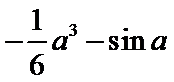
当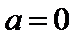
当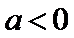
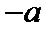
考查方向
解题思路
(1)根据定义域,单调性的概念判断单调区间(2)利用导数与函数的性质计算证明求得
易错点
分类讨论错误,计算能力弱
21.(本小题满分14分)
在平面直角坐标系xOy中,已知椭圆C:


(Ⅰ)求椭圆C的方程;
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|. 设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求
正确答案
(Ⅰ)


解析
(1)由椭圆的离心率为
又当

所以
则此椭圆方程为:
(II)设
联立方程
由

根据韦达定理可得,
又
因为
所以
令
所以
令
当



因此
等号当且仅当

所以
由(*)得 

故
设
则
所以

从而



综上所述:当



考查方向
解题思路
(1)根据所给已知条件,求出相关参数。(2)利用三角函数的边界值,求出最小值
易错点
计算能力弱