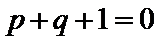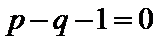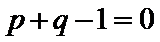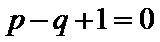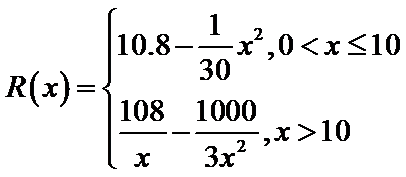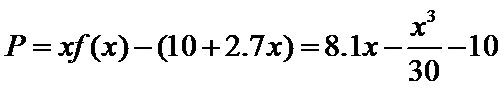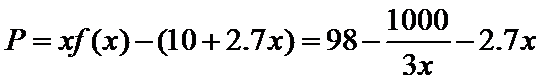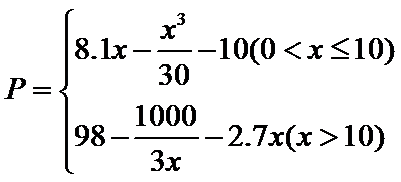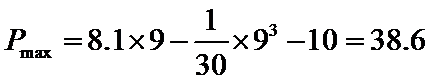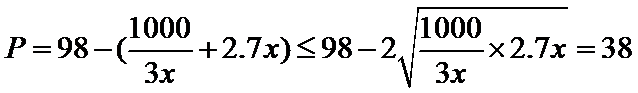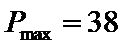- 真题试卷
- 模拟试卷
- 预测试卷
3.已知


正确答案
解析
∵sinαcosα=





知识点
9.下图是函数

正确答案
解析
由函数f(x)=x2+ax+b的部分图象得0<b<1,f(1)=0,从而-2<a<-1,
而g(x)=lnx+2x+a在定义域内单调递增,g(

∴函数g(x)=lnx+f′(x)的零点所在的区间是(
知识点
1.已知全集


正确答案
解析
解集合N的不等式
知识点
2.点P从(1,0)出发,沿单位圆

正确答案
解析
点P从(1,0)出发,沿单位圆逆时针方向运动弧长到达Q点,所以∠QOx= 




知识点
4.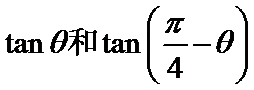
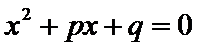
正确答案
解析
因为tanθ和tan(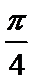
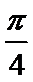
tanθtan(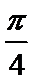
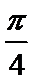
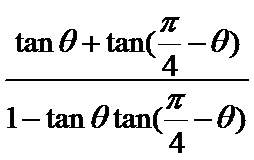
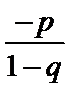
得到p-q+1=0故选D
知识点
5.已知

正确答案
解析
∵sinαcosα=





知识点
6.曲线

正确答案
解析
y′= 



即y=

故答案为A
知识点
7.函数的图象大致为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数
正确答案
解析
由题意,阴影部分E由两部分组成
因为函数y=



=1+ln2故选D.
知识点
10.已知函数



①
②若

③

④若对

其中正确命题的个数为( )
正确答案
解析
函数f(x)=x3+ax2+bx+c的图象过原点,可得c=0;又f′(x)=3x2+2ax+b,且f(x)在x=±1处的切线斜率均为-1,则有
①可见f(x)=x3-4x是奇函数,因此①正确;x∈[-2,2]时,[f′(x)]min=-4,则k≤f'(x)恒成立,需k≤-4,因此④错误.
②令f′(x)=0,得x=±



因此②错误;
且f(x)的极大值为f(-



所以f(x)的最大值为M=

知识点
11.已知定义在R上的可导函数


正确答案
1
解析
据题意知f′(1)=- 




故答案为1
知识点
13.设

正确答案
解析
由题意f0(x)=sinx,f1(x)=f0′(x)=cosx,f2(x)=f1′(x)=-sinx,
f3(x)=f2′(x)=-cosx,f4(x)=f3′(x)=sinx,
由此可知,在逐次求导的过程中,所得的函数呈周期性变化,从0开始计,周期是4,
∵2015=4×503+3,故f2015(x)=f3(x)=-cosx∴f2015(


知识点
15.下列五个函数中:①






正确答案
②③
解析
要使当0<x1<x2<1时,使f(

可得对任意两点A(x1,f(x1)),B (x2,f(x2)),曲线f(x)在A,B两点横坐标的中点的纵坐标,大于A、B两点的纵坐标的一般,也就是说f(x)的图象“上凸”可以画出①②③④⑤的图象进行判断:
在0<x1<x2<1上为上凸的图象:
可以看见②③的图象是上凸的,对于⑤可以进行研究:y=cos2x,周期T=π,要求在0<x1<x2<1上是上凸的,
如上图:在(

综上:②③是使f(

知识点
12.已知
正确答案
解析
因为cos(


知识点
14.已知直线


正确答案
-1
解析
设切点坐标为(m,n)y'|x=m= 
∴n=0,而切点(1,0)又在直线y=x+a上∴a=-1故答案为-1.
知识点
16.已知集合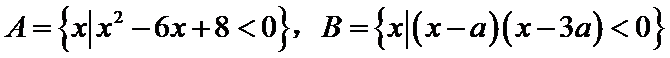
(1)若
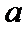
(2)若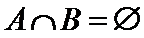
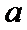
正确答案
(1)当a=0时,B=∅,不合题意.
当a>0时,B={x|a<x<3a},要满足题意,则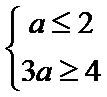
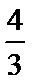
当a<0时,B={x|3a<x<a},要满足题意,则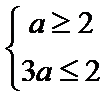
综上,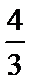
(2)要满足A∩B=∅,当a>0时,B={x|a<x<3a},
则a≥4或3a≤2,即0<a≤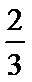
当a<0时,B={x|3a<x<a},则a≤2或a≥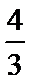
当a=0时,B=∅,A∩B=∅.综上所述,a≤
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数


(1)求实数
(2)若不等式
(3)定义在










正确答案
(1)∵函数g(x)=ax2-2ax+1+b,因为a>0,
所以g(x)在区间[2,3]上是增函数,
又∵函数g(x)故在区间[2,3]上的最大值为4,最小值为1,

(2)由已知可得f(x)=g(|x|)=x2-2|x|+1为偶函数,
所以不等式f(log2k)>f(2)可化为|log2k|>2,解得k>4或0<k<
(3)函数f(x)为[1,3]上的有界变差函数.因为函数f(x)为[1,3]上的单调递增函数,
且对任意划分T:1=x0<x1<…<xi<…<xn=3有f(1)=f(x0)<f(x1)<…<f(xI)<…<f(xn)=f(3)
所以|f(xi)-f(xi-1)|=f(x1)-f(x0)+f(x2)-f(x1)<…<f(xn)-f(xn-1)
=f(xn)-f(x0)=f(3)-f(1)=4恒成立,
所以存在常数M,使得
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)求
(2)若

正确答案
(1)函数


=sin(4x+

(2)由(1)得:f(α)=sin(4α+
由于



cos(4α+
所以cos4α=cos[(4α+





解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)当

(2)若
(3)当a=0,求使方程
正确答案
(1)∵ex>0,
∴当f(x)>0时即ax2+x>0,
又∵a<0,
∴原不等式可化为x(x+
∴f(x)>0的解集为(0,-
(2)∵f(x)=(ax2+x)ex,
∴f,(x)=(2ax+1)ex+(ax2+x)ex=[ax2+(2a+1)x+1]ex,
①当a=0时,f,(x)=(x+1)ex,∵f,(x)≥0在[-1,1]上恒成立,当且仅当x=-1时取“=”,
∴a=0满足条件;
②当a≠0时,令g(x)=ax2+(2a+1)x+1,
∵△=(2a+1)2-4a=4a2+1>0,
∴g(x)=0有两个不等的实根x1、x2,
不妨设x1>x2,因此f(x)有极大值和极小值;
若a>0,∵g(-1)•g(0)=-a<0,∴f(x)在(-1,1)内有极值点,∴f(x)在[-1,1]上不单调;
若a<0,则x1>0>x2,
∵g(x)的图象开口向下,要使f(x)在[-1,1]单调递增,由g(0)=1>0,
∴


综上可知,a的取值范围是[-
(3)当a=0时,方程f(x)=x+2为xex=x+2,
∵ex>0,∴x=0不是原方程的解,
∴原方程可化为ex-
令h(x)=ex-

∴h(x)在(-∞,0)和(0,+∞)上是单调增函数;又h(1)=e-3<0,h(2)=e2-2>0,
h(-3)=e-3
∴方程f(x)=x+2有且只有两个实根,且分别在区间[1,2]和[-3,-2]上,
所以,整数k的所有值为{-3,1}.
解析
解析已在路上飞奔,马上就到!
知识点
18.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为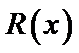
(1)写出年利润W(万元)关于年产量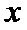
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。
(注:年利润=年销售收入-年总成本)
正确答案
(1)当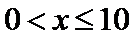
当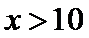
(2)①当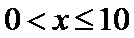
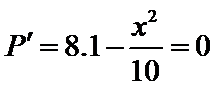
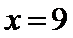
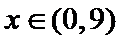
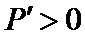
当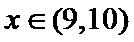
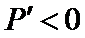
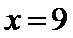
②当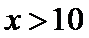
当且仅当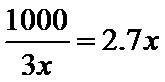
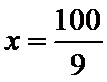
综合①、②知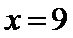
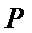
所以当年产量为9千件时,该企业生产此产品获利最大
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)求
(2)设
正确答案
(1)把x=
f(





(2)由f(3α+


代入得:2sin[



2sin[





又α,β∈ [0,
所以cosα=

则cos(α+β)=cosαcosβ-sinαsinβ=



解析
解析已在路上飞奔,马上就到!