- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在正三棱柱




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的外接球的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.直线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某程序框图如图所示,则该程序运行后输出的值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知
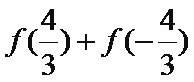
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.正定中学教学处采用系统抽样方法,从学校高三年级全体800名学生中抽50名学生做学习状况问卷调查。现将800名学生从1到800进行编号,在

正确答案
55
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知向量







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知等差数列







(1)求数列
(2)求数列


正确答案
(1)因为






又当


当


所以数列


所以
(2)因为
则

由①-②,得
整理,得
解析
解析已在路上飞奔,马上就到!
知识点
18. 某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户每月的碳排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少
(1)求所选的两个小区恰有一个为“非低碳小区”的概率;
(2)假定选择的“非低碳小区”为小区


正确答案
(1)设三个“非低碳小区”为
用

则从5个小区中任选两个小区,所有可能的结果有10个,它们是









用







故所求概率为
(2)由图1可知月碳排放量不超过
由图2可知,三个月后的低碳族的比例为
所以三个月后小区
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)求函数
(2)若函数

①求实数
②若对于



正确答案
(1)
由









(2)
①由(1)知,

又






经验证,当


②
易知


由①知
当



故



而

















综上,所求实数

解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分。
22. 选修4-1:几何证明选讲
已知









(1)证明:
(2)若

23.选修4-4:坐标系与参数方程
在极坐标系内,已知曲线





(1)求曲线

(2)设点



24.选修4—5:不等式选讲
已知常数



正确答案
22.(1)∵ PA是切线,AB是弦,∴ ∠BAP=∠C,
又 ∵ ∠APD=∠CPE,
∴ ∠BAP+∠APD=∠C+∠CPE,
∵ ∠ADE=∠BAP+∠APD,
∠AED=∠C+∠CPE,∴ ∠ADE=∠AED.
(2)由(1)知∠BAP=∠C,
又 ∵ ∠APC=∠BPA,
∴ △APC∽△BPA, ∴
∵ AC=AP, ∴ ∠APC=∠C=∠BAP,由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,
∵ BC是圆O的直径,∴ ∠BAC=90°, ∴ ∠APC+∠C+∠BAP=180°-90°=90°,
∴ ∠C=∠APC=∠BAP=




23.解:(1) 对于曲线

可化为直角坐标方程

对于曲线


可化为普通方程
(2) 过圆心





因此两条切线所成角的余弦值的取值范围是
24. 解: (1)若
因为
(2)若
因为
因为


综上,有由(1)(2)可知,解集为
解析
解析已在路上飞奔,马上就到!
知识点
19. 在直三棱柱




(1)求证:
(2)若




正确答案
(1)证明:



又






又 









(2)在直三棱柱







在



在
由(1)知





解析
解析已在路上飞奔,马上就到!
知识点
20. 在平面直角坐标系






(1)写出
(2)设过点










正确答案
(1)由题设知
根据椭圆的定义,



设其方程为
则




(2)依题设直线





设


设



即
因为


令

当


当


综上得点

解析
解析已在路上飞奔,马上就到!